Volumes of Prisms Cylinders Objectives 1 To find

Volumes of Prisms & Cylinders Objectives: 1) To find the volume of a prism. 2) To find the volume of a cylinder.

Volume ► Volume – Is the space that a figure occupies. § Measured in cubic units. ►cm 3, in 3, m 3, ft 3

Finding the volume of a Prism – 2 parallel bases and faces are rectangles. Cross sections are congruent to the bases. What is a Cross section? ► Prism V = Bh Height (h) Area of Base or Cross Section A = lw (Rectangle) Area of Base (B) Height of Prism
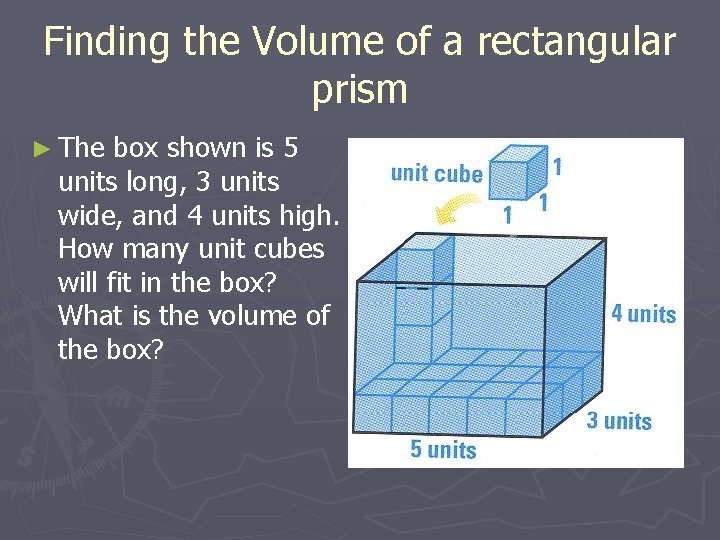
Finding the Volume of a rectangular prism ► The box shown is 5 units long, 3 units wide, and 4 units high. How many unit cubes will fit in the box? What is the volume of the box?

Find the Volume of the Prism Area of Base B = l • w 10 in V = Bh = (3 in • 5 in)(10 in) = (15 in 2)(10 in) 3 in 5 in = 150 in 3

Discussion: What prism is this? the Cross Section to determine. can’t you use l • w • h? 3 in 8 in 10 in V = Bh = ½bh • h = ½(8 in) 3 in __ • (10 in) = (12 in 2) • (10 in) = 120 in 3 Look at Why
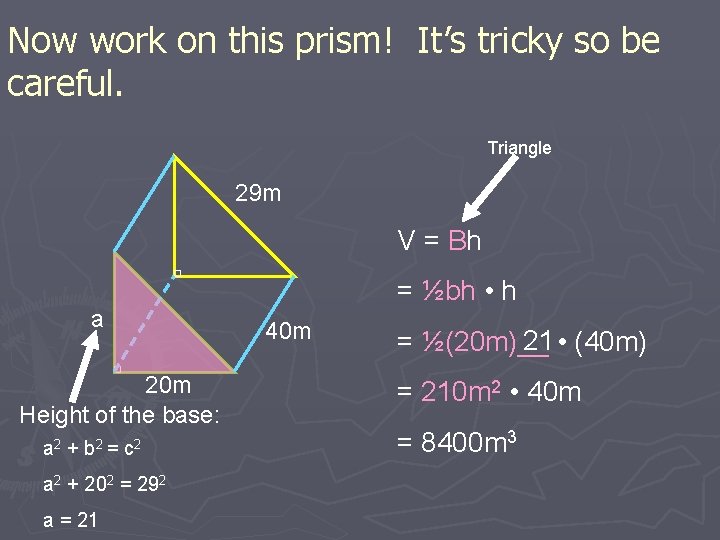
Now work on this prism! It’s tricky so be careful. Triangle 29 m V = Bh a 20 m Height of the base: a 2 + b 2 = c 2 a 2 + 202 = 292 a = 21 = ½bh • h 40 m 21 • (40 m) = ½(20 m)__ = 210 m 2 • 40 m = 8400 m 3
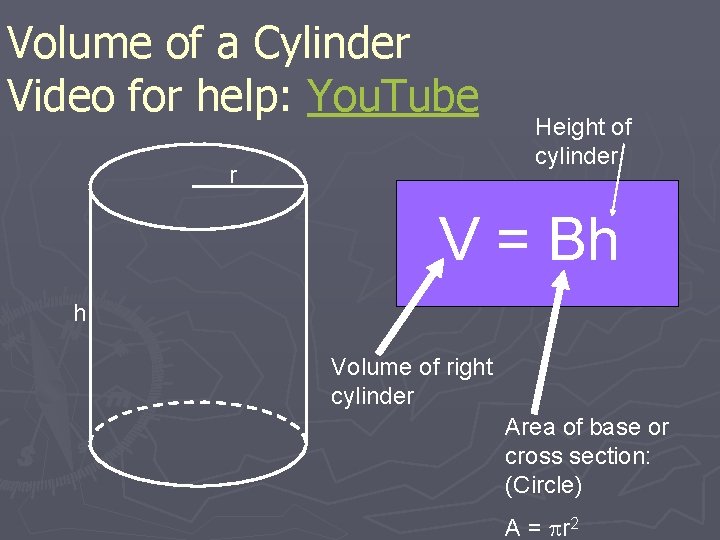
Volume of a Cylinder Video for help: You. Tube r Height of cylinder V = Bh h Volume of right cylinder Area of base or cross section: (Circle) A = r 2
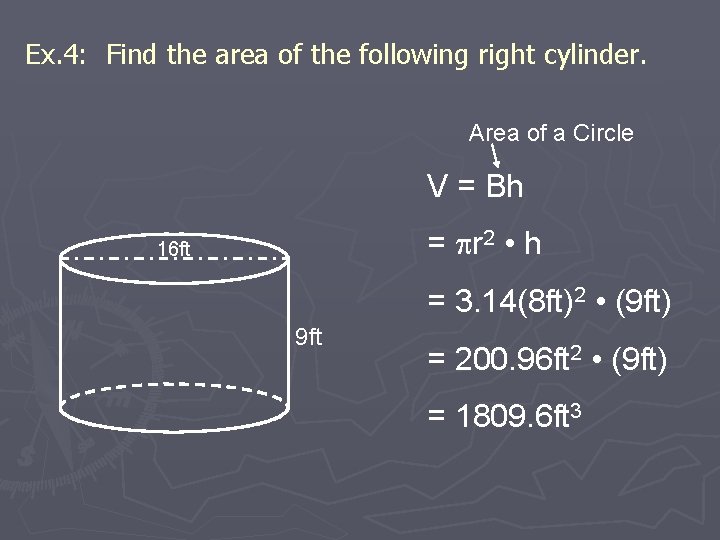
Ex. 4: Find the area of the following right cylinder. Area of a Circle V = Bh = r 2 • h 16 ft = 3. 14(8 ft)2 • (9 ft) 9 ft = 200. 96 ft 2 • (9 ft) = 1809. 6 ft 3

Ex. 5: Find the volume of the following composite figure. Half of a cylinder: Vc = Bh = r 2 • h = (6 in)2 • (4 in) = 452 in 3 11 in 4 in = 452/2 = 226 in 3 12 in VT = V c + V p Volume of Prism: = 226 in 3 + 528 in 3 = (11)(12)(4) = 754 in 3 = 528 in 3 Vp = Bh
What have we learned? ? Volume of a prism or a cylinder: V = Bh Capitol “B” stands for area of the base. Composite Figures: Made up of two separate solids.
- Slides: 11


















