Vektormez szingulris pontjainak indexe A topolgia differencilegyenleteknl hasznlt

Vektormező szinguláris pontjainak indexe A topológia differenciálegyenleteknél használt egyszerű alkalmazásai Vegyünk egy vektormezőt az irányított euklideszi síkon, melyen adva van egy irányított, zárt görbe. Feltétel: a görbe ne menjen át a vektormező szinguláris pontjain Miközben egy pont pozitív irányban körbejárja a görbét, az adott pontban a mező vektora folytonosan elcsavarodik.

A görbe indexe: A vektor forgásszámát a mező bejárásakor a görbe indexének nevezzük. • Az index előjele attól függ, hogy a vektor a sík irányítása által adott irányba fordul-e. – Ha igen, akkor +, ha nem, akkor – • Mennyi az alábbi görbék indexe?

Az index tulajdonságai 1. Tulajdonság: Egy zárt görbe indexe a görbe folytonos deformálásával nem változik, amíg nem megy keresztül szinguláris pontokon. 2. Tulajdonság: A görbe indexe nem változik a vektormező folytonos deformációjánál, ha a deformáció közben a görbén nincs szinguláris pont.

Tekintsünk egy síkbeli vektormezőt. Legyen adott rajta egy D körlap, melynek S a határoló vonala (a körvonal). Tétel: Ha az S görbe indexe különbözik 0 -tól, akkor az általa határolt D tartományban legalább egy szinguláris pont van. Bizonyítás: A tulajdonságok alapján Ha valóban nincs egyetlen szinguláris pont sem a D-n, akkor folytonosan deformálható anélkül, hogy változna az indexe. Így összehúzható egy pontba. Az így kapott kicsiny görbe indexe 0. Mivel a deformálásnál nem ez nem változott, ezért kezdetben is 0 volt.

Feladat Adott a komplex síkon (O pont kivételével) Számítsuk ki a és a görbe a vektormező. görbe indexét, ha növekedése irányába van irányítva. Megoldás Míg körbejárjuk egyszer a görbét, tehát a vektor pontosan n-szer fodul körbe. A görbe indexe n. alatt

Bebizonyítjuk az algebra alaptételét. Bármely egyenletnek legalább egy komplex gyöke van. Tekintsük a komplex síkon a v(z) vektormezőt! Az egyenlet gyökei a v(z) vektormező szinguláris pontjai. Lemma Tekintsük vektormezőnek a Legyen képletet, ami az eredeti v(z) mezőbe való folytonos deformálása a kör sugara. esetén.

(r >1 volt!) Ezért az r sugarú körön a deformáció teljes ideje alatt nincsenek szinguláris pontok. soha nem lesz 0. Tehát a kör indexe megegyezik vt(z) és v(z) vektormezőben. A görbe indexe n, tehát van szinguláris pont, létezik a egyenletnek gyöke.

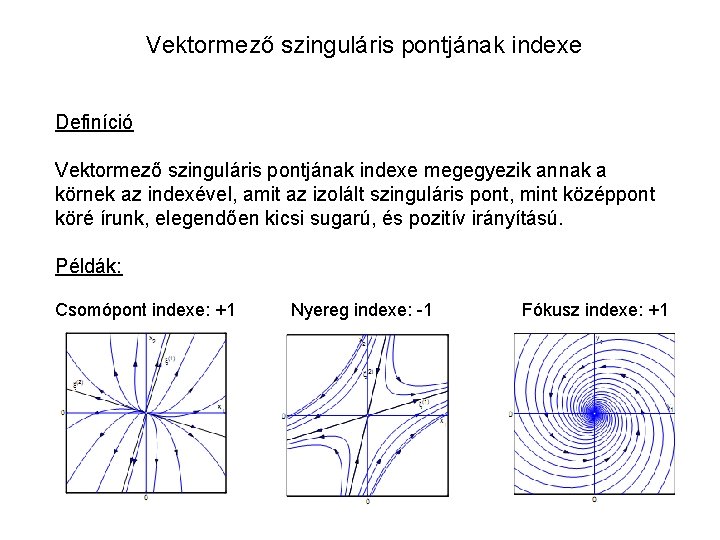
Vektormező szinguláris pontjának indexe Definíció Vektormező szinguláris pontjának indexe megegyezik annak a körnek az indexével, amit az izolált szinguláris pont, mint középpont köré írunk, elegendően kicsi sugarú, és pozitív irányítású. Példák: Csomópont indexe: +1 Nyereg indexe: -1 Fókusz indexe: +1

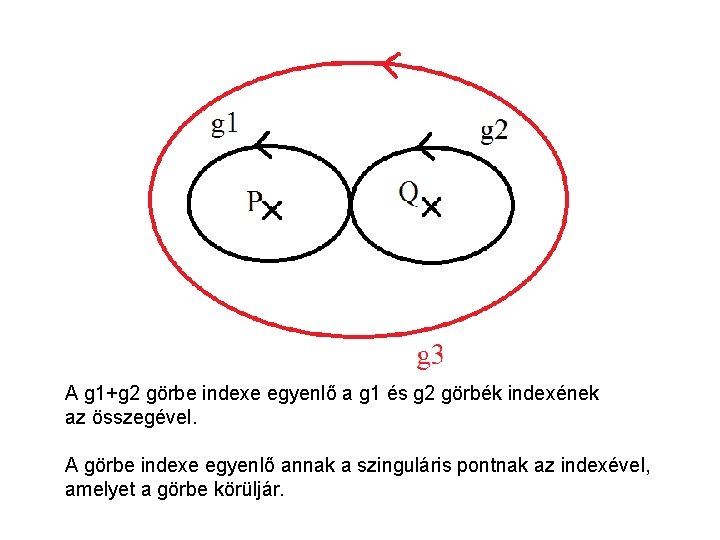
Tétel az indexek összegéről. Legyen D az irányított sík egy kompakt tartománya, amelyet az S görbe határol. S görbe indexe egyenlő a D belsejében fekvő szinguláris pontok összegével. Szemléltetés: Tekintsünk két irányított görbét, g 1 -et és g 2 -t, amelyek egy ponton mennek keresztül. Képezzük az új g 1+g 2 görbét úgy, hogy először g 1 -en haladunk végig, majd g 2 -n!

A g 1+g 2 görbe indexe egyenlő a g 1 és g 2 görbék indexének az összegével. A görbe indexe egyenlő annak a szinguláris pontnak az indexével, amelyet a görbe körüljár.

A szinguláris pontok indexeinek összege gömbfelületen Tétel: Síkbeli vektormező szinguláris pontjainak indexe változatlan marad diffeomorfizmus során. Következmény: az index geometriai fogalom, amely független a koordinátarendszertől. (elég egy térképen kiszámítani) Tekintsünk egy gömbfelületet és tegyük fel, hogy adott rajta olyan vektormező, amelynek kizárólag izolált szinguláris pontjai vannak. Ekkor számuk véges, lévén a gömbfelület kompakt. Tétel: Az összes szinguláris pont indexének az összege független a mező választásától és ez az összeg 2.

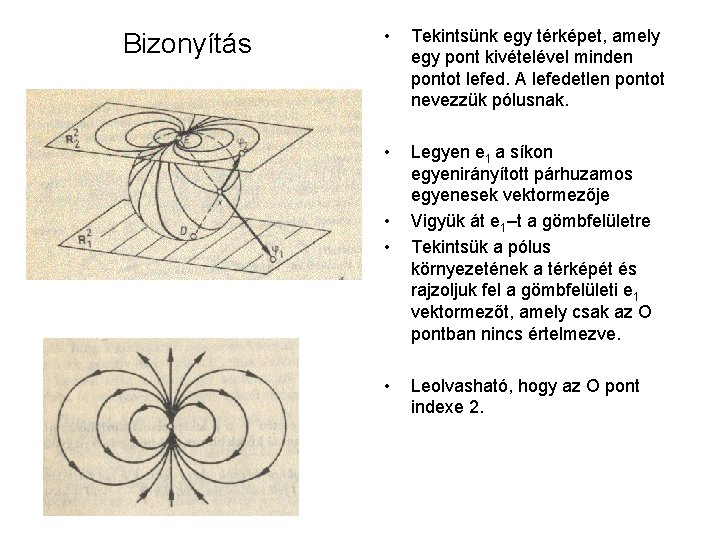
Bizonyítás • Tekintsünk egy térképet, amely egy pont kivételével minden pontot lefed. A lefedetlen pontot nevezzük pólusnak. • Legyen e 1 a síkon egyenirányított párhuzamos egyenesek vektormezője Vigyük át e 1–t a gömbfelületre Tekintsük a pólus környezetének a térképét és rajzoljuk fel a gömbfelületi e 1 vektormezőt, amely csak az O pontban nincs értelmezve. • • • Leolvasható, hogy az O pont indexe 2.

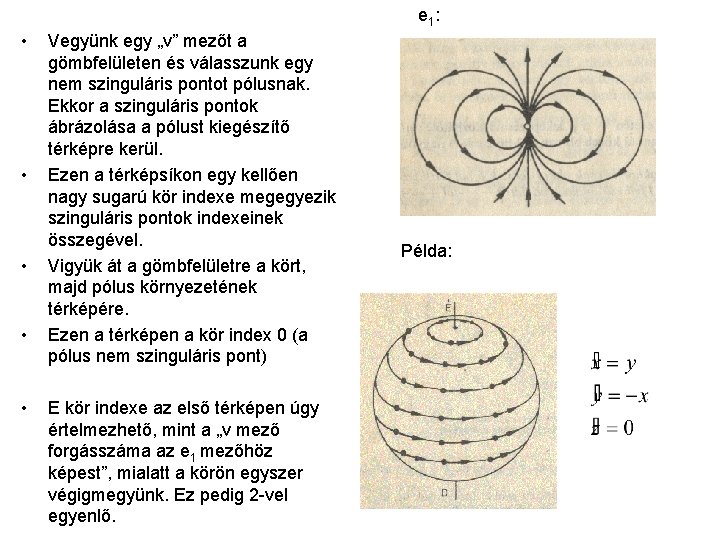
e 1 : • • • Vegyünk egy „v” mezőt a gömbfelületen és válasszunk egy nem szinguláris pontot pólusnak. Ekkor a szinguláris pontok ábrázolása a pólust kiegészítő térképre kerül. Ezen a térképsíkon egy kellően nagy sugarú kör indexe megegyezik szinguláris pontok indexeinek összegével. Vigyük át a gömbfelületre a kört, majd pólus környezetének térképére. Ezen a térképen a kör index 0 (a pólus nem szinguláris pont) E kör indexe az első térképen úgy értelmezhető, mint a „v mező forgásszáma az e 1 mezőhöz képest”, mialatt a körön egyszer végigmegyünk. Ez pedig 2 -vel egyenlő. Példa:

Következmény: sima függvény a gömbfelületen. Ha a minimumhelyeket és a maximumhelyek számát összeadjuk és levonjuk a nyeregpontok számát, akkor 2 -t kapunk. (Példa: Föld) Megjegyzések: • Sziget esetén ez az összeg 1 lesz. • Euler poliédertétele: korlátos, komplex poliéderre: #csúcsok - #élek + #lapok = 2 • Sokaság Euler karakterisztikája: kétdimenziós kompakt sokaságon definiált vektormező szinguláris pontjai indexeinek az összege