UNIVERSIDAD TCNICA FEDERICO SANTA MARA VALPARASO CHILE DEPARTAMENTO

UNIVERSIDAD TÉCNICA FEDERICO SANTA MARÍA VALPARAÍSO, CHILE DEPARTAMENTO DE ELECTRÓNICA INTRODUCCIÓN A LA LÓGICA PROGRAMABLE Manuel Díaz Rosales Estudiante Ingeniería Civil Electrónica

FUNCIONES BOOLEANAS El algebra de Boole es el lenguaje matemático de los sistemas digitales. Las operaciones del algebra de Boole deben regirse por propiedades y reglas lógicas llamados leyes o postulados. Estos postulados se pueden usar para demostrar leyes más generales sobre expresiones booleanas.

ÁLGEBRA DE BOOLE: POSTULADOS Clausura: a + b esta en B, a • b esta en B Conmutatividad: a + b = b + a, a • b = b • a Asociatividad: a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Identidad: a + 0 = a, a • 1 = a Distributividad: a + (b • c) = (a + b) • (a + c) a • (b + c) = (a • b) + (a • c) Complementariedad: a + a’ = 1, a • a’ = 0

ÁLGEBRA DE BOOLE: TEOREMAS Con la formulación de los postulados del algebra de Boole se pueden demostrar varias proposiciones o teoremas de algebra booleana Para las demostraciones de teoremas se pueden usar tablas de verdad, postulados y teoremas ya demostrados

ÁLGEBRA DE BOOLE: TEOREMAS Definición: El algebra de Boole es un sistema algebraico cerrado que contiene un conjunto B de dos elementos {0, 1} y tres operadores {・, +, ‘}. Igualdad: Dos expresiones son iguales si una puede ser substituida por otra.

ÁLGEBRA DE BOOLE: TEOREMAS Identidad: 1. X + 0 = X D. X • 1 = X Nulo (elementos únicos): 2. X + 1 = 1 D. X • 0 = 0 Idempotencia: 3. X + X = X D. X • X = X Involución: 4. (X’)’ = X Complementariedad: 5. X + X’ = 1 D. X • X’ = 0

ÁLGEBRA DE BOOLE: TEOREMAS

ÁLGEBRA DE BOOLE: TEOREMAS Morgan: 14. (X + Y +. . . )’ = X’ • Y’ • . . . 14 D. (X • Y • . . . )’ = X’ + Y’ +. . . Morgan generalizado: 15. f’(X 1, X 2, . . . , Xn, 0, 1, +, • ) = f(X 1’, X 2’, . . . , Xn’, 1, 0, • , +) establece relaciones entre • y +

ÁLGEBRA DE BOOLE: EJEMPLO Demuestre este teorema: X • Y + X • Y’ = X Igualdad Distributividad (8) Complementariedad (5) Identidad (1 D) X • Y + X • Y’ = X • (Y + Y’) = X • (1) =X

ÁLGEBRA DE BOOLE: EJERCICIO Demuestre este teorema : X + X • Y = X

ÁLGEBRA DE BOOLE: EJERCICIO Demuestre este teorema : X + X • Y = X Igualdad, identidad (1 D) Distributividad (8) Identidad (1 D) X+X • Y=X • 1+X • Y = X • (1 + Y) = X • (1) =X

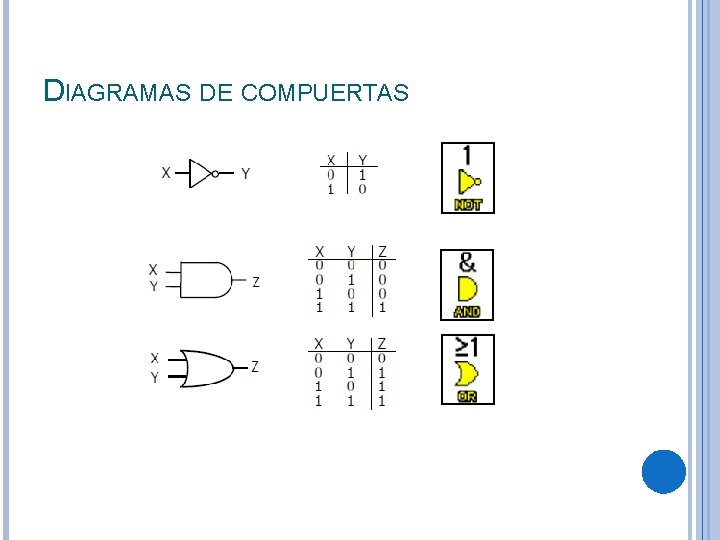
DIAGRAMAS DE COMPUERTAS

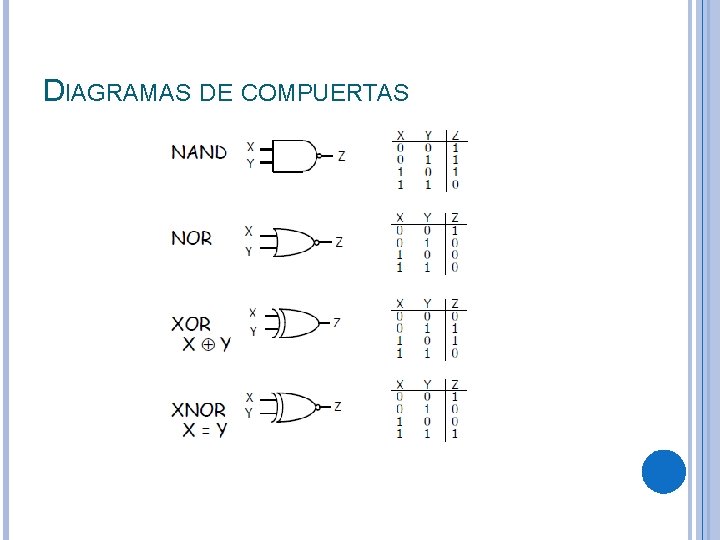
DIAGRAMAS DE COMPUERTAS

PLC: CONTROLLER LOGIC PROGRAM

PLC: AL 2 -14 MR-A 8 entradas (2 análogas) 6 salidas tipo Relé Carga máxima de 250[V]

BLOQUES Display Comparador Flip-Flop Conversor AD

BLOQUES Botones Calculadora