TRIGONOMETRIC EQUATIONS Firstly recall the graphs of y

TRIGONOMETRIC EQUATIONS

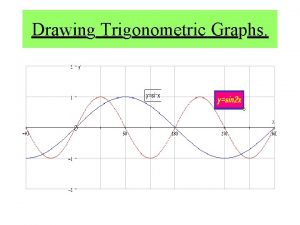
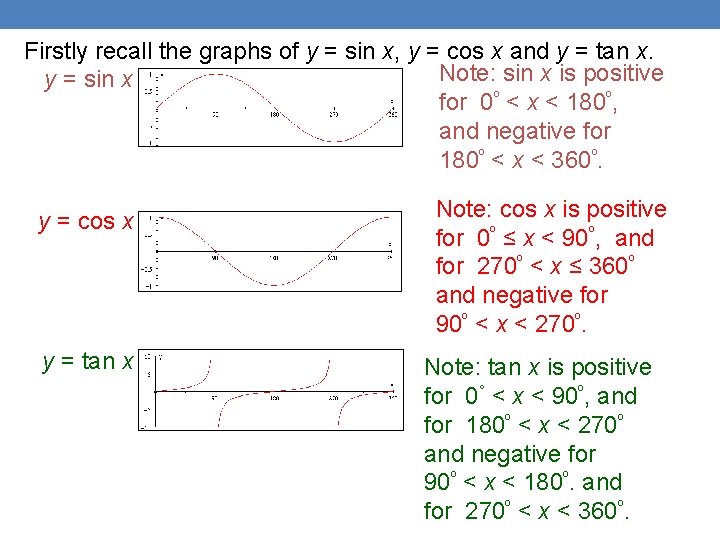
Firstly recall the graphs of y = sin x, y = cos x and y = tan x. Note: sin x is positive y = sin x for 0º < x < 180º, and negative for 180º < x < 360º. y = cos x y = tan x Note: cos x is positive for 0º ≤ x < 90º, and for 270º < x ≤ 360º and negative for 90º < x < 270º. Note: tan x is positive for 0° < x < 90º, and for 180º < x < 270º and negative for 90º < x < 180º. and for 270º < x < 360º.

We can summarise the information in the following diagram: 90º sin +ve cos –ve cos +ve tan –ve tan +ve º º 180 0 , 360º sin –ve cos +ve tan –ve 270º This can be simplified to show just the positive ratios: 90º S A sin +ve all +ve or just: 180º 0º, 360º T C tan +ve cos +ve 270º

The positive ratio diagram can be used to solve trigonometric equations: Example 1: Solve cos x = 0. 5; 0º ≤ x < 360º Using: S A T C We can see that the cosine of an angle is positive in the two quadrants on the right, i. e. the 1 st and 4 th quadrants. α = cos– 1 0. 5= 60º Hence the solutions in the given range are: x = 60°, 360 – 60° so x = 60º, 300º

Example 2: Solve sin x = – 0. 5; – 360º < x ≤ 360º The sine of an angle is negative in the 3 rd and 4 th quadrants. α = sin– 1 0. 5= 30º N. B. The negative is ignored to find the acute angle. Hence the solutions in the given range are: x = – 150°, – 30°, 210°, 330° In problems where the angle is not simply x, the given range will need to be adjusted.

Example 3: Solve 3 + 5 tan 2 x = 0; 0º ≤ x ≤ 360º. Firstly we need to make tan 2 x the subject of the equation: 3 tan 2 x =– 5 The tangent of an angle is negative in the 2 nd and 4 th quadrants. = 30. 96° The range must be adjusted for the angle 2 x. i. e. 0° ≤ 2 x ≤ 720°. Hence: 2 x = 149. 04°, 329. 04°, 509. 04°, 689. 04°. x = 74. 5°, 164. 5°, 254. 5°, 344. 5°.

Example 4: Solve 2 sin (4 x + 90º) – 1 = 0; 0 < x < 90º sin (4 x + 90º) The sine of an angle is positive in the 1 st and 2 nd quadrants. = 30º The range must be adjusted for the angle 4 x + 90º. i. e. 0º < 4 x < 360º 90º < 4 x + 90º < 450º 4 x + 90º = 150°, 390° 4 x = 60º, 300º x = 15º, 75º

Example 5: Solve 6 sin 2 x + sin x – 1 = 0; 0º ≤ x < 360º A quadratic equation! It may help to abbreviate sin x with s: i. e. 6 s 2 + s – 1 = 0 Factorising this: (3 s – 1)(2 s + 1)= 0 α = 19. 47º º α = 30 So, x = 19. 5°, 160. 5°, 210°, 330°. (To nearest 0. 1º. )

Summary of key points: To solve a Trigonometric Equation: • Re-arrange the equation to make sin, cos or tan of some angle the subject. • Locate the quadrants in which the ratio is positive, or negative as required. Using: S A T C • Adjust the range for the given angle. • Read off all the solutions within the range.