TRASFORMAZIONI GEOMETRICHE DEF 1 Si dice trasformazione ogni

TRASFORMAZIONI GEOMETRICHE DEF. 1 - Si dice trasformazione ogni corrispondenza biunivoca tra i punti del piano. DEF. 2 - Se si considera il piano riferito ad un sistema di assi cartesiano Oxy 1

DEF. 2 - Una trasformazione si dice involutoria se l'immagine dell'immagine di ogni punto del piano è il punto stesso. DEF. 3 - Un punto P si dice punto unito della trasformazione se ha come immagine se stesso. DEF. 4 – Una retta r si dice globalmente unita nella trasformazione se ogni punto di r ha come immagine un punto di r. DEF. 5 – Una retta r si dice retta di punti uniti se è costituita tutta di punti uniti. DEF. 6 - Si dice trasformazione identica e la si indica con I la trasformazione che ad ogni punto del piano fa corrispondere se stesso. DEF. 7 – Una trasformazione T applicata ad una figura del piano, ad esempio un triangolo, si dice diretta (inversa) se conserva (non conserva) il verso di lettura dei vertici del triangolo. DEF. 8 –L'applicazione inversa T-1 di una trasformazione T è una trasformazione tale che T T-1 = I , cioè equivale all'identità. Composizione di trasformazioni - Date le trasformazioni T 1 e T 2 , la trasformazione T 1 T 2 e T 2 T 1 sono le trasformazioni composte. In generale: T 1 T 2 T 1 N. B. (T 1 T 2)-1 = T 2 -1 T 1 -1. 2

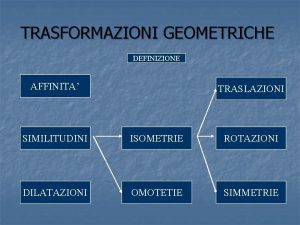
ISOMETRIE DEF - Si dice isometria una trasformazione che conserva la distanza tra i punti. Teorema - La trasformazione inversa di una isometria è una isometria. Teorema - Il composto di due isometrie è una isometria. Sono isometrie: TRASLAZIONI SIMMETRIE CENTRALI SIMMETRIE ASSIALI 3

OMOTETIE DEF - Dato un punto O(0, 0) ed un numero reale k 0, si dice omotetia di centro O e rapporto k la trasformazione che ad ogni punto P del piano associa un punto P' tale che OP' = k OP. SIMILITUDINI DEF. – Si dice similitudine una trasformazione geometrica S che sia composizione di un’isometria e di un’omotetia. Risulta costante il rapporto delle distanze tra punti corrispondenti 4

INVARIANTI DELLE TRASFORMAZIONI ISOMETRIA OMOTETIA SIMILITUDINE Allineamento dei punti Lunghezza dei segmenti Rapporto tra i segmenti Ampiezza degli angoli 5

AFFINITA’ DEF - Si dice affinità una trasformazione che conserva il parallelismo. Sono affinità: DILATAZIONI Teorema - Una isometria è un’affinità. Teorema - Una omotetia è un’affinità. Teorema - Una similitudine è un’affinità. PROIETTIVITA’ DEF - Si dice proiettività una trasformazione che conserva l’allineamento. 6

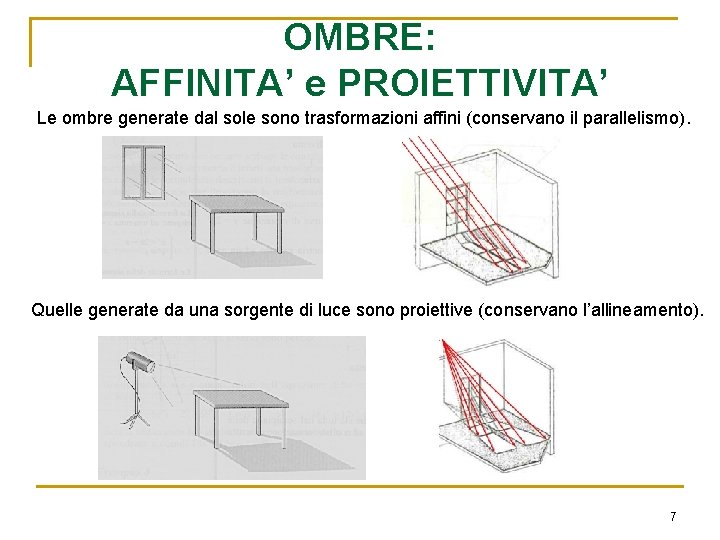
OMBRE: AFFINITA’ e PROIETTIVITA’ Le ombre generate dal sole sono trasformazioni affini (conservano il parallelismo). Quelle generate da una sorgente di luce sono proiettive (conservano l’allineamento). 7

DALL’AFFINE AL PROIETTIVO PUNTI IMPROPRI Le proiettività portano rette in rette. Ma la corrispondenza non è propriamente una corrispondenza biunivoca. In questo esempio i binari si incontrano in un punto che non esiste, un punto all’infinito. La geometria proiettiva utilizza dunque un piano, il piano proiettivo, dotato di altri punti: i punti all'infinito o punti impropri, il cui insieme costituisce la cosiddetta retta impropria. In questo modo si amplia il concetto di punto e di retta. Nel piano proiettivo non esistono rette parallele. Da qui la nascita della prospettiva. 8

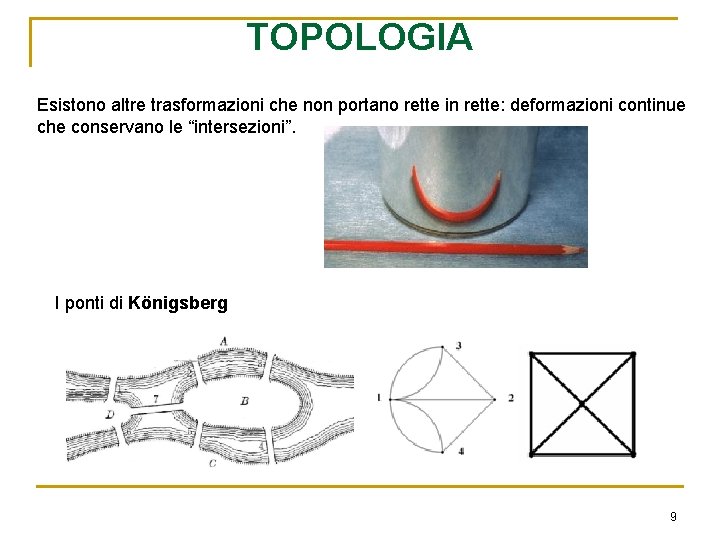
TOPOLOGIA Esistono altre trasformazioni che non portano rette in rette: deformazioni continue che conservano le “intersezioni”. I ponti di Königsberg 9

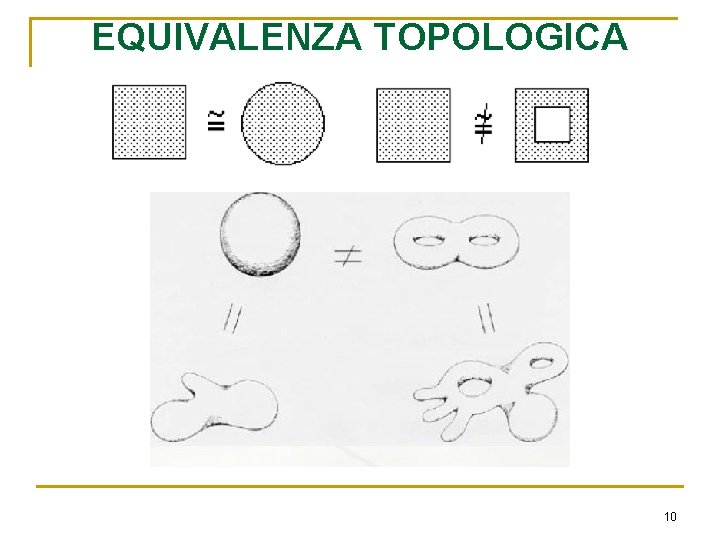
EQUIVALENZA TOPOLOGICA 10

11