Todennkisyyslaskenta 5 Todennkisyysjakaumia T 055403 1 5 1

Todennäköisyyslaskenta 5. Todennäköisyysjakaumia T 055403 1

5. 1 Yleistä Satunnaismuuttuja x on diskreetti, jos se voi saada vain tiettyjä erillisiä arvoja x 1, x 2, … , xn, joita vastaavat tietyt pistetodennäköisyydet p 1, p 2, … , pn. T 055403 2

Satunnaismuuttuja x on jatkuva, mikäli sen arvojoukko on reaalilukujen joukko R tai sen jokin osaväli. Muuttujan tyypin mukaan puhutaan joko diskreetistä tai jatkuvasta jakaumasta. T 055403 3

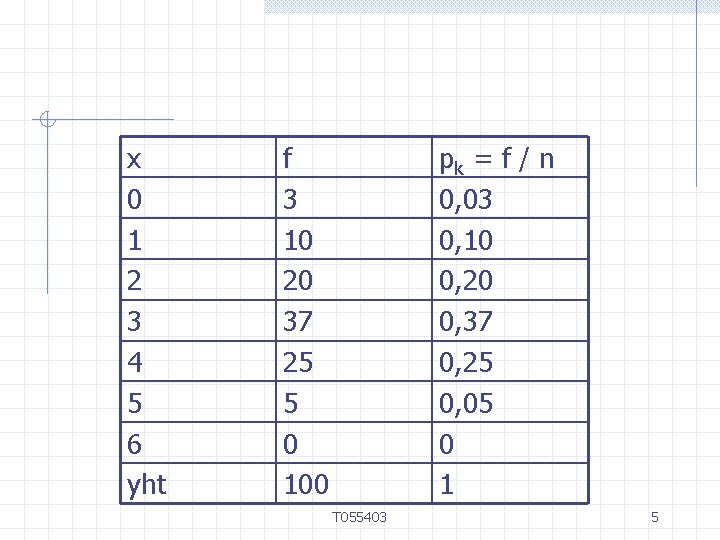
5. 2 Diskreetti jakauma Esimerkki 1. 100 kuusilapsista perhettä osallistui tutkimukseen, jossa tutkittiin perheen tyttöjen määrää. Saatiin seuraavanlainen empiirinen tutkimustulos: T 055403 4

x 0 1 2 3 4 5 6 yht f 3 10 20 37 25 5 0 100 pk = f / n 0, 03 0, 10 0, 20 0, 37 0, 25 0, 05 0 1 T 055403 5

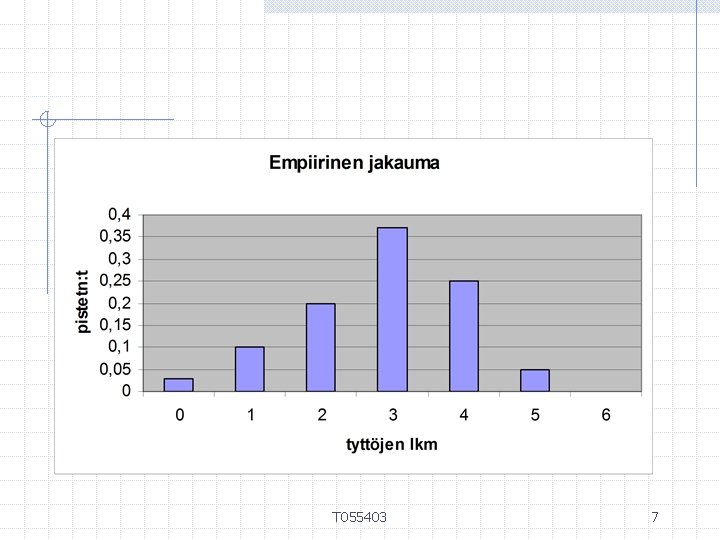
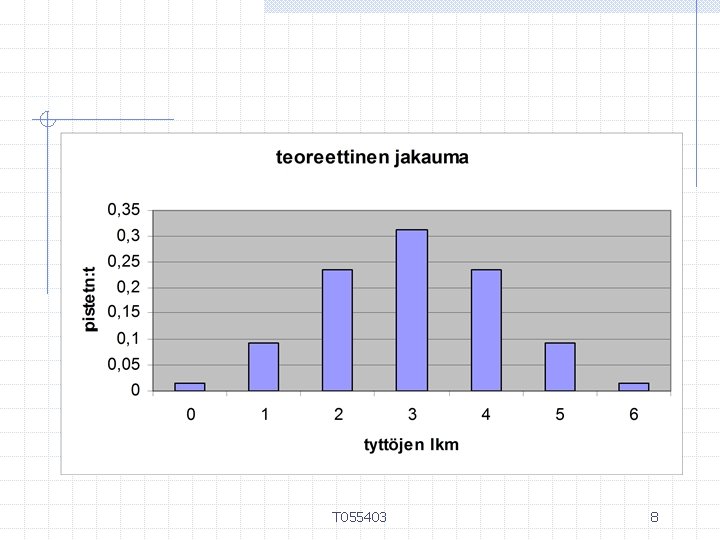
Esitä empiirinen jakauma pylväsdiagrammina. Laske teoreettinen jakauma ja esitä sekin pylväsdiagrammien avulla. Vertaa jakaumia toisiinsa. T 055403 6

T 055403 7

T 055403 8

Teoreettinen jakauma on ns. binomijakauma. Merkitään x Bin (n, p). T 055403 9

Odotusarvo ja keskihajonta Diskreetin satunnaismuuttujan x odotusarvo eli keskiarvo saadaan laskettua, kun tunnetaan satunnaismuuttujan arvot ja niitä vastaavat pistetodennäköisyydet: T 055403 10

Keskihajonta Dx = kertoo, kuinka paljon satunnaismuuttujan x arvot keskimäärin poikkeavat keskiarvosta. Keskihajonnan neliö on nimeltään varianssi, jota merkitään T 055403 11

Diskreetin satunnaismuuttujan x keskihajonta saadaan laskettua, kun tunnetaan satunnaismuuttujan arvot ja niitä vastaavat pistetodennäköisyydet sekä odotusarvo : T 055403 12

Binomijakauman tunnusluvut Binomijakauman odotusarvolle ja keskihajonnalle voidaan johtaa seuraavat kaavat: T 055403 13

Esimerkki 2. Määritä esimerkin 1 empiirisen jakauman ja teoreettisen jakauman odotusarvo ja keskihajonta. T 055403 14

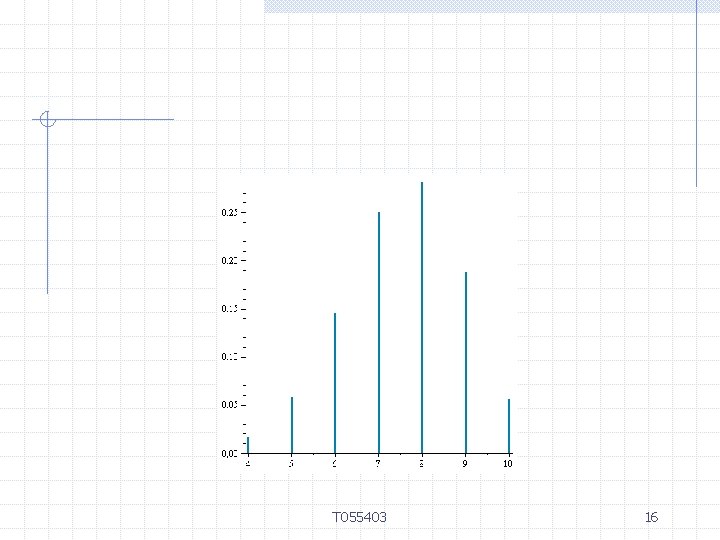
Esimerkki 3. Olkoon x Bin (10, 3/4). Määritä Ex ja Dx. T 055403 15

T 055403 16

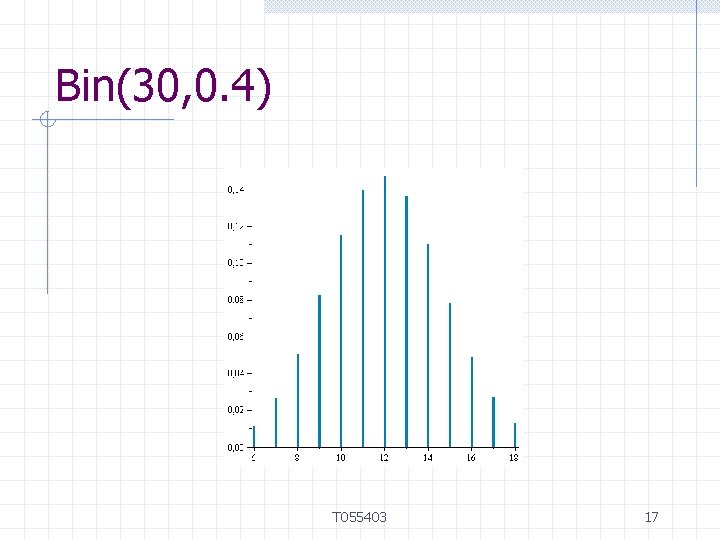
Bin(30, 0. 4) T 055403 17

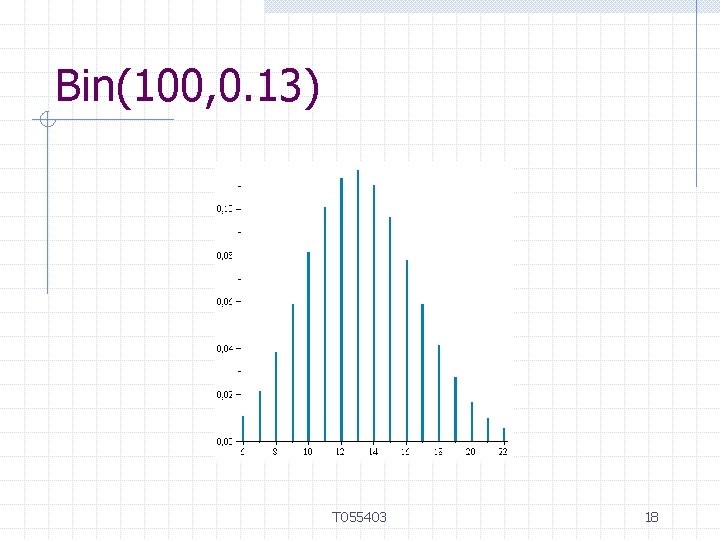
Bin(100, 0. 13) T 055403 18

Poisson-jakauma Binomitodennäköisyyden käyttäytymistä tutkimalla on mahdollista osoittaa, että suorittamalla ”rajaprosessin” antamalla n , jolloin p 0, odotusarvo pysyy vakiona (merk. ). T 055403 19

Mikäli satunnaismuuttujan x arvojoukko on N, ja jos satunnaismuuttujan pistetodennäköisyydet ovat T 055403 20

niin sanotaan, että x on Poissonjakautunut parametrina . Poisson-jakauma on tärkeä, sillä sitä voidaan soveltaa tilanteisiin, joissa ollaan kiinnostuneita sattumiskertojen lukumäärästä esim. pituus- tai aikayksikköä kohden. T 055403 21

Erityisesti tämä malli on käyttökelpoinen, kun lukumäärällä ei ole mitään ylärajaa (esimerkiksi tuotteen virheiden lukumäärä). T 055403 22

Poisson-jakauman odotusarvo ja keskihajonta: T 055403 23

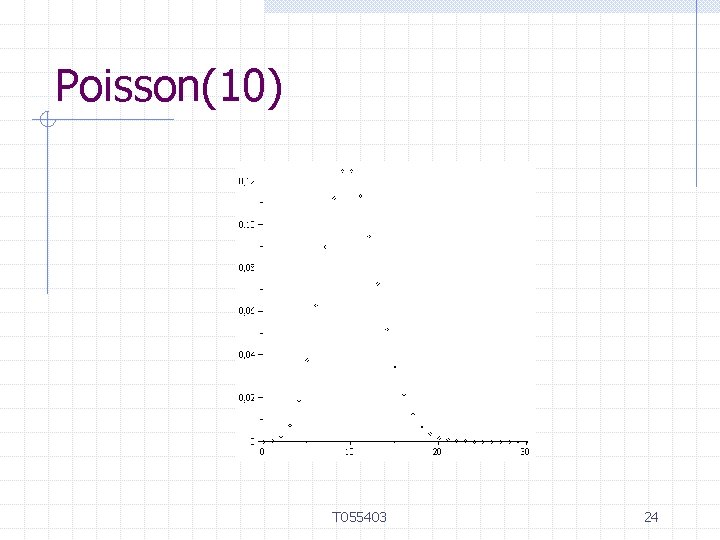
Poisson(10) T 055403 24

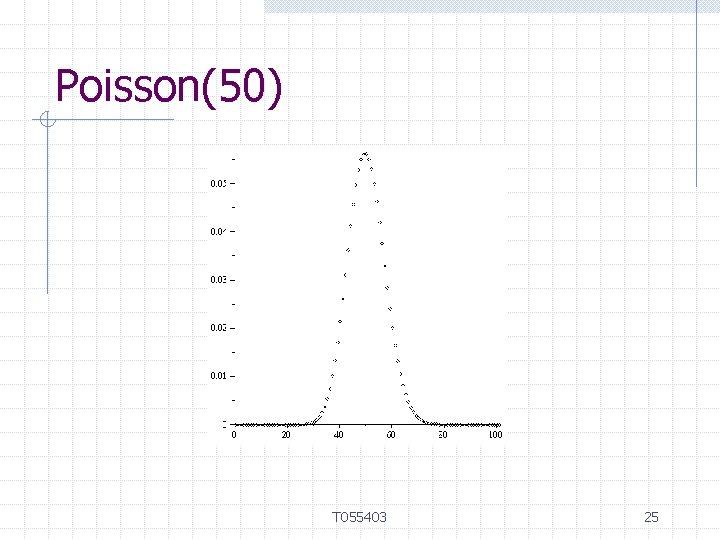
Poisson(50) T 055403 25

Esimerkki 4. Eräässä kaupungissa on havaittu, että sähkökatkoksia sattuu vuosittain keskimäärin 17 kertaa. Millä todennäköisyydellä kuukauden aikana sähkökatkoksia on enemmän kuin 2? T 055403 26

Esimerkki 5. Tehtaan mukaan kondensaattori täyttää laatuvaatimukset tn: llä 0, 999. Mikäli kondensaattoreita ostetaan 500 kpl pakkauksissa, niin millä todennäköisyydellä erässä on enintään 4 viallista? T 055403 27