Some examples in Cournot Competition Cournot Duopoly A

Some examples in Cournot Competition

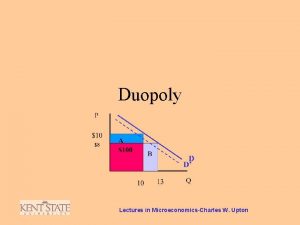
Cournot Duopoly A duopoly with inverse demand P = a-b. Q (P/Q: market price/quantity) ¢ ci: the constant marginal cost of Firm i ¢ Each firm chooses qi to max. its profit ¢ Firm 1 chooses q 1 to Max (a-b. Q-c 1)q 1 ¢ Firm 2 chooses q 2 to Max (a-b. Q-c 2)q 2 ¢

A simultaneous-move game ¢ N. E. (q 1*, q 2*) solves the simultaneous eqs. (2 first-order conditions) a-2 bq 1 -bq 2 -c 1 = 0 -------(A) a-bq 1 -2 bq 2 -c 2 = 0 -------(B) ¢ q 1*=(a-2 c 1+c 2)/3 b ¢ q 2*=(a+c 1 -2 c 2)/3 b ¢

Stackelberg Competition ¢ ¢ ¢ A similar game where Firm 1 acts first with his actions observed by Firm 2. (A leader and a follower in the same industry. A sequential-move game) From Firm 2’s F. O. C, equation (B), Firm 2’s best response to every q 1 is q 2=(a-bq 1 -c 2)/(2 b) →q 2(q 1) captures the equilibrium in every subgame of q 1 (there’s a subgame after Firm 1 announces q 1 )

¢ ¢ Firm 1 takes this into account (foreseeing that q 2=q 2(q 1)) and chooses q 1 to max its profit Max [a-b(q 1+q 2)-c 1]q 1 s. t. q 2=q 2(q 1) →simply replace q 2 with q 2(q 1) SPNE q 1*=(a-2 c 1+c 2)/(2 b) q 2*=q 2(q 1*)=(a+2 c 1 -3 c 2)/(4 b)

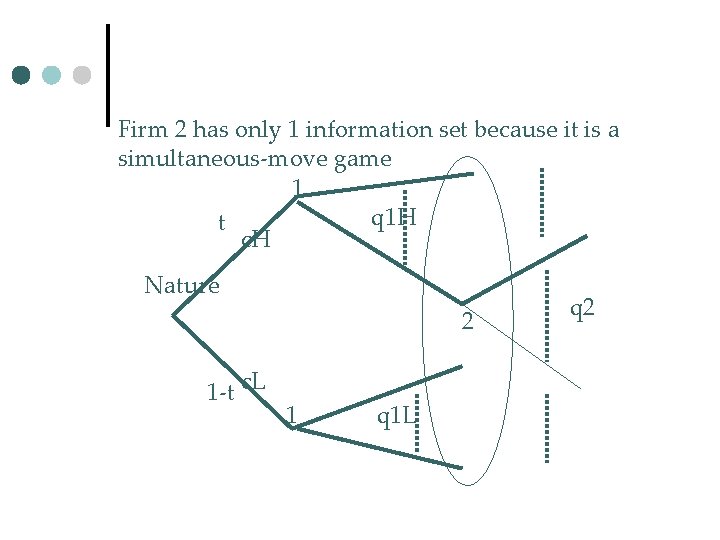
Static Cournot with asymmetric info. ¢ ¢ The problem with asymmetric info. →the game is no longer common knowledge Static (Simultaneous-move) Bayesian Games (Harsanyi) Assume with probability t, c 1=c. H, and (1 -t) c 1=c. L. (Firm 1 also knows this is how Firm 2 expects Firm 1’s costs though Firm 1 knows exactly its own cost. First consider a slightly different game where even Firm 1 doesn’t know its own cost before the game is played but soon it will realize after the nature has made a choice. So that we can interpret the original game in this way.

Firm 2 has only 1 information set because it is a simultaneous-move game 1 q 1 H t c. H Nature 2 1 -t c. L 1 q 1 L q 2

¢ ¢ ¢ A N. E. will specify what Firm 1 will do when c. H and when c. L, and what Firm 2 will do. It’s like now a 3 -player game. Indeed Firm 1 with high cost will (it competes with q 2, not q 1 L) max [a-b(q 1 H+q 2)-c. H]q 1 H →q 1 H=(a-bq 2 -c. H)/(2 b)…………. (I 1) Similary Firm 1 with low cost will max [a-b(q 1 L+q 2)-c. L]q 1 L →q 1 L=(a-bq 2 -c. L)/(2 b)…………. . (I 2)

Firm 2 will maximize (with prob. t it’s competing with q 1 H, and 1 -t with q 1 L) t[a-bq 1 H-bq 2 -c 2]q 2+(1 -t)[a-bq 1 L-bq 2 c 2]q 2 →q 2=[a-c 2 -tbq 1 H-(1 -t)bq 1 L]/(2 b)…(I 3) ¢ The N. E. is (q 1 H, q 1 L, q 2) that solves (I 1), (I 2) and (I 3) simultaneously. ¢

q 2*=[a-2 c 2+tc. H+(1 -t)c. L]/(3 b] q 1 H*=[2 a+2 c 2 -(3+t)c. H-(1 -t)c. L]/(6 b) q 1 L*=[2 a+2 c 2 -tc. H-(4 -t)c. L]/(6 b) ¢ One can compare the result to the deterministic cases with low-cost/high -cost Firm 1 to see the differences in price/quantity. ¢

¢ We’ll see a similar game when we introduce auction where all players have private information regarding its own valuation toward to item on auction and they have to bid simultaneously.