Solvency II introduction Solvency II is a new
















- Slides: 21

Solvency II – introduction Solvency II is a new regime which changes fundamentally the insurers (and reinsurers). The insurers have to operate risk-based and it has a lot of new regulations and standards. The Solvency II. comes into force at 01. 2016. The actuaries are affected most of all the new reserving methodology and the new SCR, MCR calculation. Insurance mathematics III. lecture

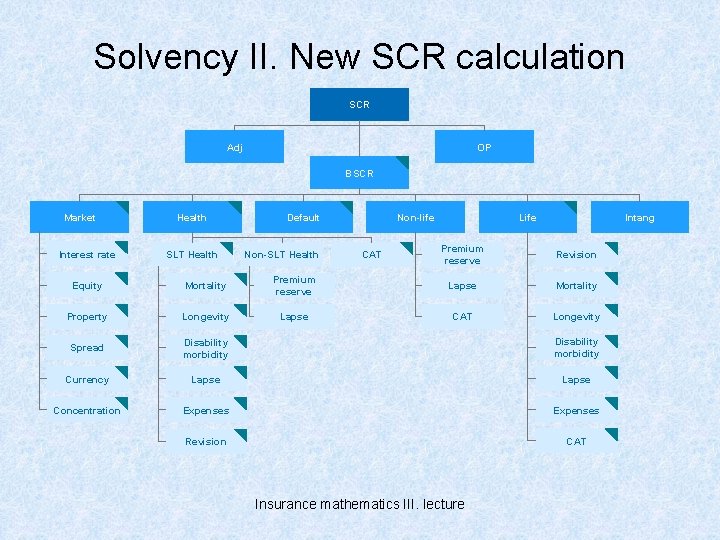
Solvency II. New SCR calculation SCR Adj OP BSCR Market Interest rate Health SLT Health Default Non-SLT Health Non-life CAT Life Intang Premium reserve Revision Equity Mortality Premium reserve Lapse Mortality Property Longevity Lapse CAT Longevity Spread Disability morbidity Currency Lapse Concentration Expenses Revision CAT Insurance mathematics III. lecture

Solvency II. Reserving methodology is based on the best estimate assumptions plus additional risk margin. The best estimate shall correspond to the probabilityweighted average of future cash-flows within the contract boundary, taking account of the time value of money (expected present value of future cash-flows), using the relevant risk-free interest rate term structure. Insurance mathematics III. lecture

Solvency II. Reserving II. The risk margin shall be such as to ensure that the value of the technical provisions is equivalent to the amount that insurance and reinsurance undertakings would be expected to require in order to take over and meet the insurance and reinsurance obligations. Contract boundary: contract shall be taking into consideration till the date when one of partners (insurer or insured) can quit from policy without any consequence. In non-life section the typical possibility to exiting from policy is 1 year, it means that usually we have to calculate premium till end of first policy year – but claims according to first policy year can be reported later. Insurance mathematics III. lecture

Solvency II. Reserving III. In non-life section we can calculate separately reserve for premium and claims. The ultimate reserve will be the sum of reserve for premium and reserve for claims. The reserve for premium can be calculated with the next formula: Remark: if the product is profitable then the amount has negative sign. Insurance mathematics III. lecture

Solvency II. Reserving IV. where UPR signs the Unearned Premium Reserve; Pb. Canc signs the probability of cancellation; Cl. Pay signs the claim payment for claims which occurred before policy anniversary; DAC signs the deferred acquisition costs; Cl. HC signs the claims handling costs for claims which occurred before policy anniversary; Main. C signs the maintenance cost which are affected till policy anniversary. Insurance mathematics III. lecture

Solvency II. Reserving V. Example: Let the total portfolio is one policy with the next data: Beginning date: 01. 10. 2014 Annual premium: 50. 000 Ft Probability of cancellation: 15% yearly Expected loss ratio: 70% Commission: 6% Claims handling costs: 9% of claim (in homework 0) Maintenance costs: 10% of premium (in homework 0) Discount rate: 5% Insurance mathematics III. lecture

Solvency II. Reserving VI. Example (continued) We are calculating the reserve for premium at 31. 12. 2014. Insurance mathematics III. lecture

Solvency II. Reserving VII. Example (continued) Reserve for claims Actuaries have to estimate reported and not yet reported claims together plus claims handling cost in the future. It shall be applied the discount rate according to year of expected claim payment. If there is no differing information (e. g. changing of portfolio) we can use previous information claims. III. lecture Insurancefor mathematics

Solvency II. Reserving VIII. One possible method is as follows: OS reserve 1. step: Calculating the ratio of previous payments related to lagging time (year, quarter year, month). 2. step: Calculating the ratio of actual OS reserve according to occurring date (year, quarter year, month). 3. step: Calculating the real OS need based on result of earlier OS reserve (e. g. result is +10% , then the real OS need is lower with 10%). 4. step: Estimating the payment of real OS need based on 1. and 2. step. 5. step: Discounting the result of 4. step with adequate discount factors. Insurance mathematics III. lecture

Solvency II. Reserving IX. Example: We have 126. 000 Ft OS reserve (according to Solvency I. ) and we have to calculate Best Estimate. 1. step: we have data from past payments according to lagging as follows: 0. year 1. year 2. year 3. year 60% 30% 9% 1% 2. step: we have data about OS reserve occurring date as follows: 2011 2012 2013 2014 1. 000 5. 000 20. 000 100. 000 Insurance mathematics III. lecture

Solvency II. Reserving X. 3. step: Result of earlier OS reserve is +5%. It means the real OS need is as follows: 2011 2012 2013 2014 4. step: Payment estimation as follows according to earlier steps: Insurance mathematics III. lecture

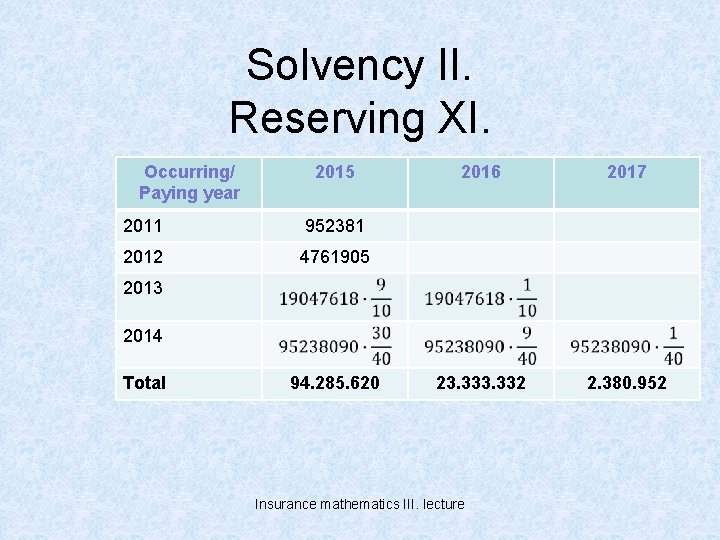
Solvency II. Reserving XI. Occurring/ Paying year 2015 2011 952381 2012 4761905 2016 2017 23. 332 2. 380. 952 2013 2014 Total 94. 285. 620 Insurance mathematics III. lecture

Solvency II. Reserving XII. 5. step: The discount rates are given as follows: 1. year 2. year 3. year 5% 4% 3% Then the reserve for OS reserve will be the next: Insurance mathematics III. lecture

Solvency II. Reserving XIII. IBNR It can be calculated with classical methods (just one difference: we have to take into consideration the result of earlier IBNR) it shall be considered which part of IBNR when will be paid (according to estimation). At the end the discount factors shall be applied. Insurance mathematics III. lecture

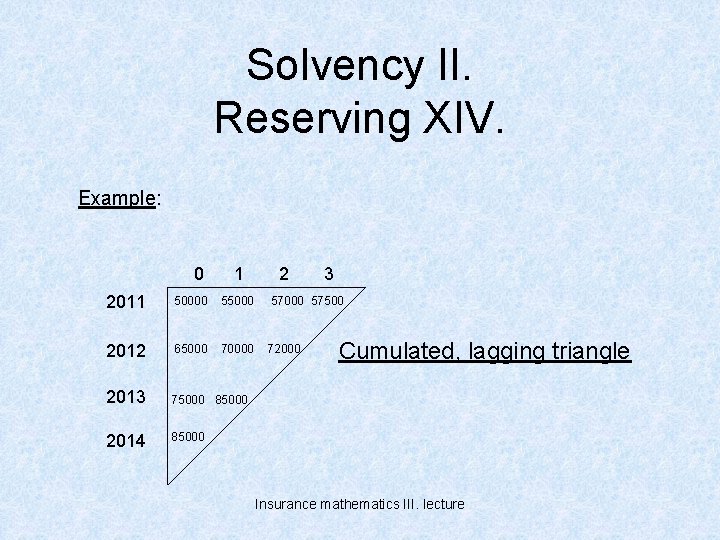
Solvency II. Reserving XIV. Example: 0 1 2 3 2011 50000 55000 57500 2012 65000 70000 72000 2013 75000 85000 2014 85000 Cumulated, lagging triangle Insurance mathematics III. lecture

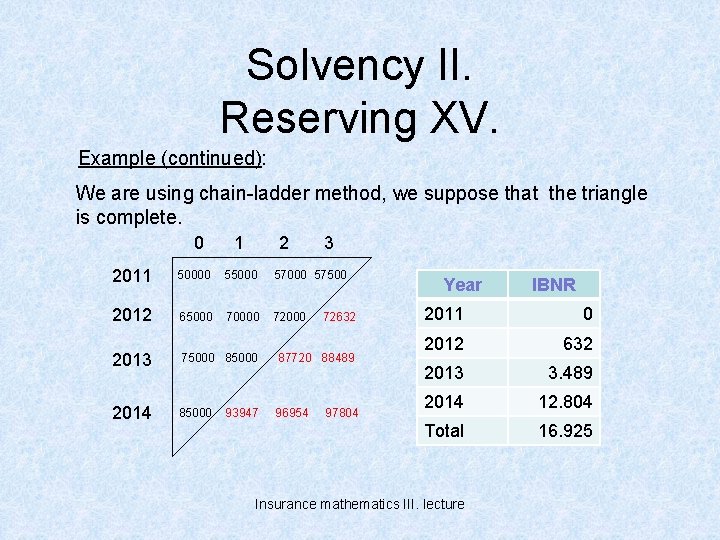
Solvency II. Reserving XV. Example (continued): We are using chain-ladder method, we suppose that the triangle is complete. 0 1 2 3 2011 50000 55000 57500 2012 65000 70000 72000 2013 75000 87720 88489 2014 85000 96954 93947 72632 97804 Year IBNR 2011 0 2012 632 2013 3. 489 2014 12. 804 Total 16. 925 Insurance mathematics III. lecture

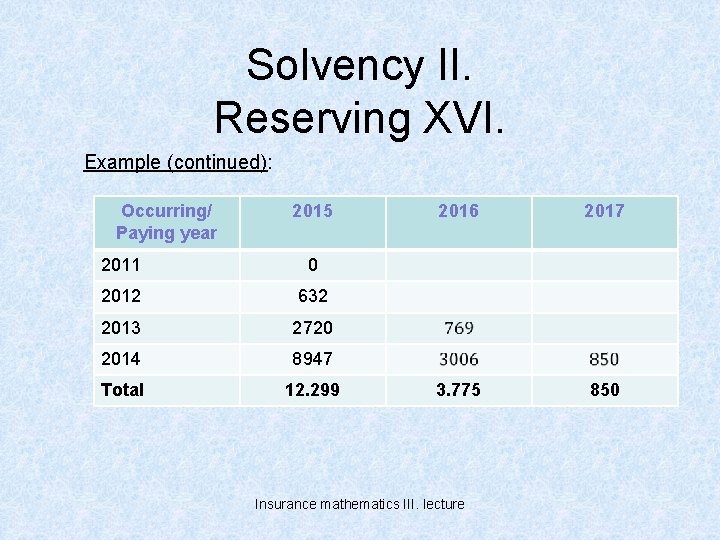
Solvency II. Reserving XVI. Example (continued): Occurring/ Paying year 2015 2011 0 2012 632 2013 2720 2014 8947 Total 12. 299 2016 2017 3. 775 850 Insurance mathematics III. lecture

Solvency II. Reserving XVII. The discount rates are given as follows: 1. year 2. year 3. year 5% 4% 3% Then the reserve for IBNR claims will be the next: Insurance mathematics III. lecture

Solvency II. Difficulties I. There a lot of questions, difficulties related to Solvency II. , because this is a total new regime and the technical specifications - which have to be applied - are not exactly clear in each case. I highlight just two points from these questions 1. Segmentation In Solvency II. the target is making homogenous risk portfolio and for these groups using the specifications. In the other side (in nonlife section) there is given the business lines which have to be applied. These two requirements would be controversy if one homogenous risk portfolio does not fit to the given business lines. Insurance mathematics III. lecture

Solvency II. Difficulties II. 2. Claim inflation There is not clear whethere is possible to consider claim inflation or not. And if the answer is yes then how should be calculated. (In EU there are countries in which has high inflation but other countries have no high inflation. ) Insurance mathematics III. lecture
 Liquidity and solvency ratios
Liquidity and solvency ratios Solvency 2 pillar 1
Solvency 2 pillar 1 Solvency ratio accounting
Solvency ratio accounting Solvency ratio accounting
Solvency ratio accounting Dampener eiopa
Dampener eiopa Define liquidity financial flexibility and solvency
Define liquidity financial flexibility and solvency Liquidity profitability and solvency
Liquidity profitability and solvency Cross-x.com
Cross-x.com Solvency ii rsr reporting
Solvency ii rsr reporting Swiss solvency test
Swiss solvency test Dr ramdhani
Dr ramdhani What is vertical financial statement analysis
What is vertical financial statement analysis Risk margin solvency ii
Risk margin solvency ii Omnibus directive
Omnibus directive Liqidity ratio
Liqidity ratio Solvency ii ppt
Solvency ii ppt Allianz solvency ii
Allianz solvency ii Solvency ii pillar 3 reporting templates
Solvency ii pillar 3 reporting templates You control your destiny you don't need magic to do it
You control your destiny you don't need magic to do it New york, new jersey, pennsylvania, and delaware
New york, new jersey, pennsylvania, and delaware Fresh oil new wine
Fresh oil new wine Marquee new hartford ny
Marquee new hartford ny