Seniority A really cool and amazing thing Seniority

Seniority A really cool and amazing thing

Seniority • First, what is it? Invented by Racah in 1942. • Secondly, what do we learn from it? • Thirdly, why do we care – that is, why not just do full shell model calculations and forget we ever heard of seniority? • Almost completely forgotten nowadays because big fast computers lessen the need for it. However, understanding it can greatly deepen your understanding of structure and how it evolves. • Start with shell structure and 2 - particle spectra – they give the essential clue.

Magic nuclei – single j configurations: jn [ e. g. , (h 11/2)2 J] Short range attractive interaction – what are the energies?

Tensor Operators Don’t be afraid of the fancy name. Ylm e. g. , Y 20 Even, odd tensors: Quadrupole Op. k even, odd To remember: (really important to know)!! δ interaction is equivalent to an odd-tensor interaction (explained in de. Shalit and Talmi)

Yo u ca n ha ve 20 0 pa ge s of th is … .

Or, this:

Seniority Scheme – Odd Tensor Operators (e. g. , magnetic dipole M 1) Fundamental Theorem *0 + even ≠ odd

Yaaaay !!!

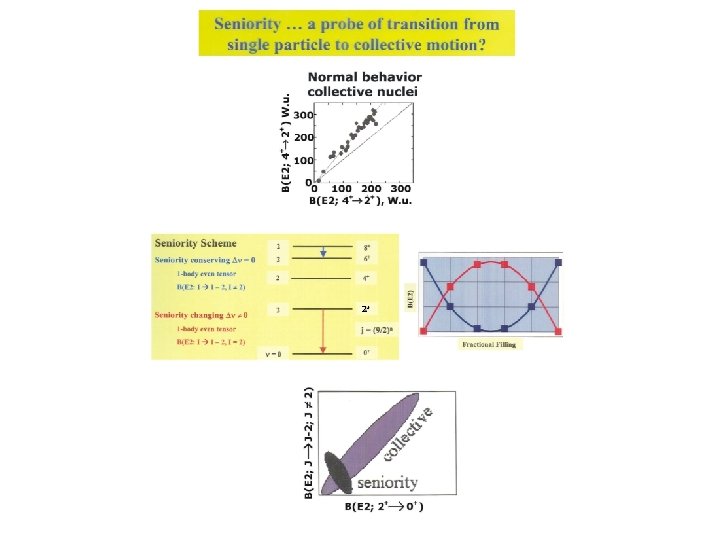
Now, use this to determine what v values lie lowest in energy. For any pair of particles, the lowest energy occurs if they are coupled to J = 0. J 0 0 lowest energy for occurs for smallest v, largest V 0 largest lowering is for all particles coupled to J = 0 lowest energy occurs for v =0 (any unpaired nucleons contribute less extra binding from the residual interaction. ) v = 0 state lowest for e – e nuclei v = 1 state lowest for o – e nuclei Generally, lower v states lie lower than high v a) g. s. of e – e nuclei have v = 0 b) Reduction formulas of ME’s jn jv achieve a huge simplification J = 0+ ! n-particle systems 0, 2 particle systems THIS is exactly the reason seniority is so useful. Low lying states have low seniority so all those reduction formulas simplify the treatment of those states enormously.

Since v = 0 ( e – e) or v = 1 ( o – e) states will lie lowest in jn configuration, let’s consider them explicitly: Starting from V 0 δαα΄ = 0 if v = 0 or 1 No 2 -body interaction in zero or 1 -body systems Hence, only second term: (n even, v = 0) (n odd, v = 1) These equations simply state that the ground state energies in the respective systems depend solely on the numbers of pairs of particles coupled to J = 0. Odd particle is “spectator”

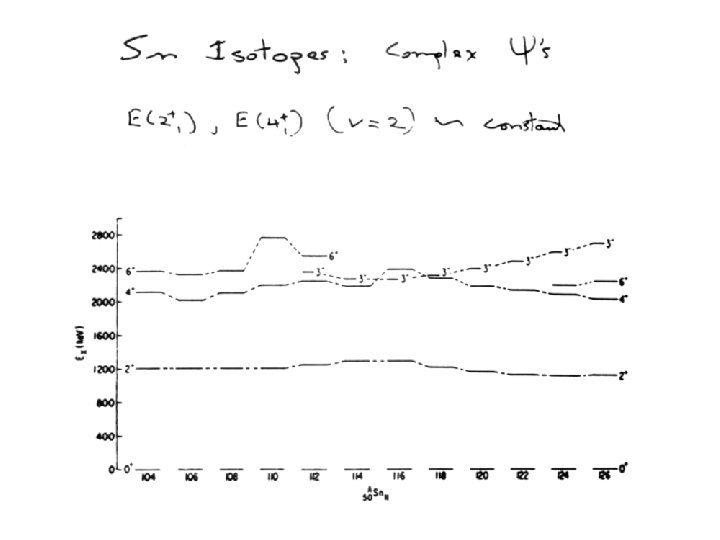
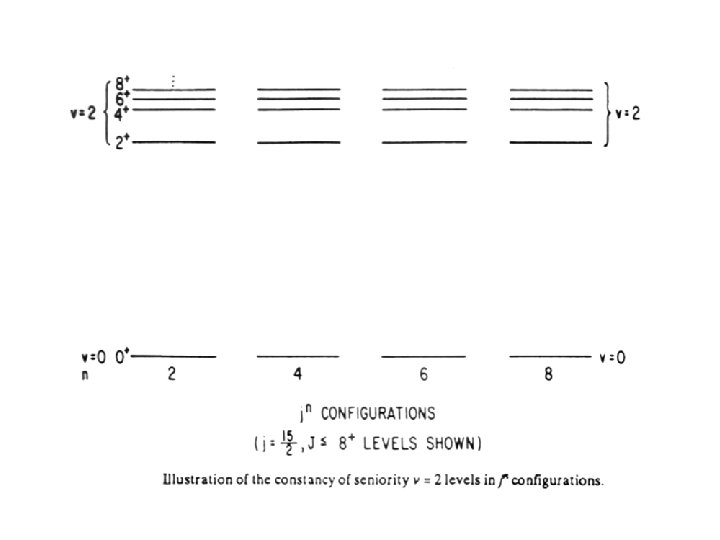
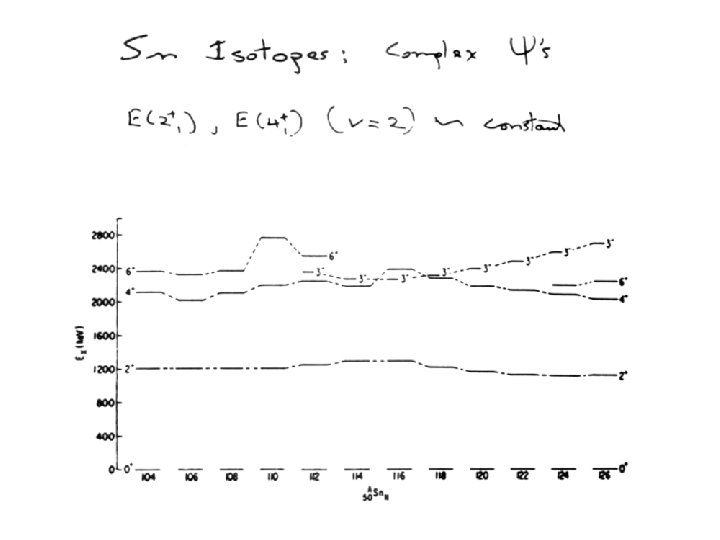
Further implications Energies of v = 2 states of jn E = Independent of n !! Constant Spacings between v = 2 states in jn (J = 2, 4, … j – 1) E = = All spacings constant ! Low lying levels of jn configurations (v = 0, 2) are independent of number of particles in orbit. Can be generalized to =

For odd tensor interactions: < j 2 ν J′│Ok│j 2 J = 0 > = 0 for k odd, for all J′ including J′ = 0 Proof: even + even ≠ odd = V 0 + Int. for J ≠ 0 No. pairs x pairing int. V 0 < 0 ν = 0 states lie lowest g. s. of e – e nuclei are 0+!! ΔE ≡ E(ν = 2, J) – E(ν = 0, J = 0) = constant ΔE│ ν ≡ E(ν = 2, J) – E(ν = 2, J ) = constant ν=2 8+ 6+ 4+ ν=2 2+ ν=0 n 0+ 2 4 6 jn Configurations 8 ν=0

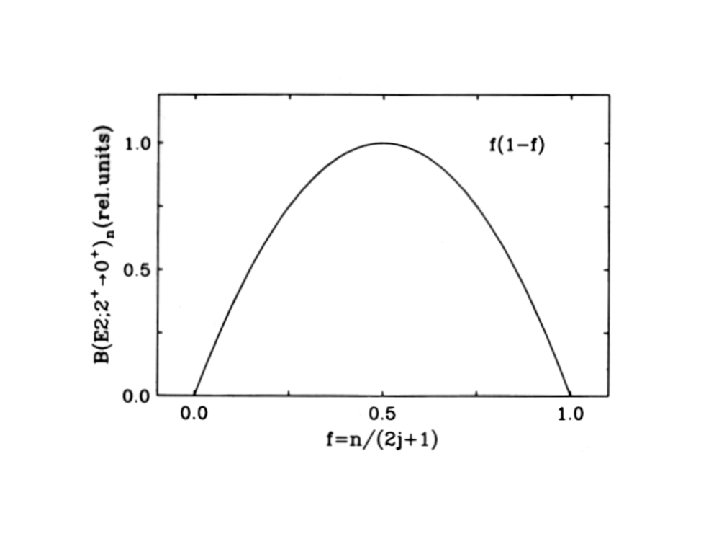
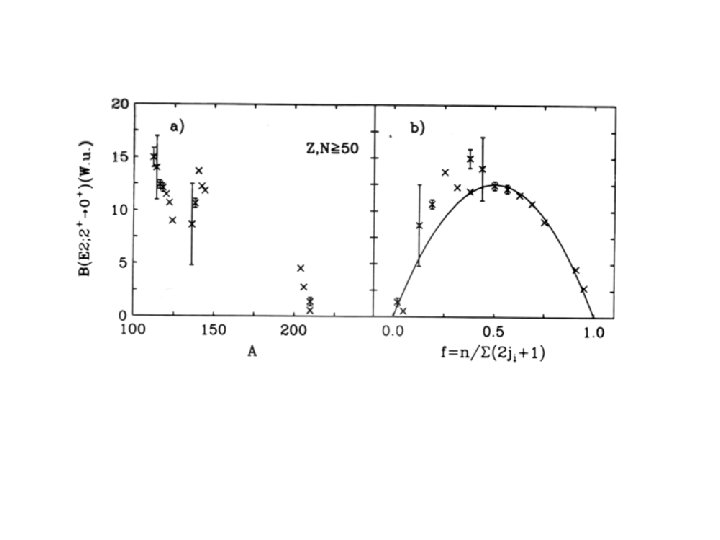
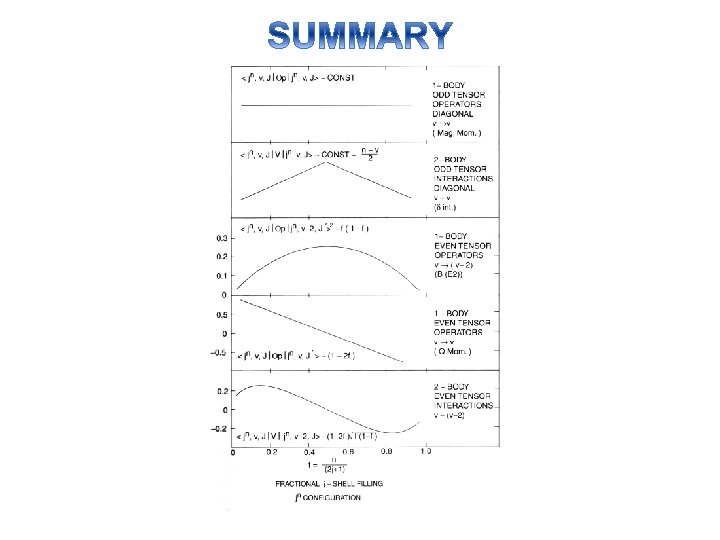
To summarize two key results: For odd tensor operators, interactions • One-body matrix elements (e. g. , dipole moments) are independent of n and therefore constant across a j shell • Two-body interactions are linear in the number of paired particles, (n – v)/2, peaking at midshell. The second leads to the v = 0, 2 results and is, in fact, the main reason that the Shell Model has such broad applicability (beyond n = 2)

So: When is seniority a good quantum number? (let’s talk about configurations) • If, for a given n, there is only 1 state of a given J Then nothing to mix with. v is good. • Interaction conserves seniority: odd-tensor interactions.

7/2 Think of levels in Ind. Part. Model: First level with j > 7/2 is g 9/2 which fills from 40 - 50. So, seniority should be useful all the way up to A~ 80 and sometimes beyond that !!!

This is why nuclei are prolate at the beginning of a shell and (sometimes) oblate at the end. OK, it’s a bit more subtle than that but this is the main reason. Another example: Consider states of a j 2 configuration: 0, 2, 4, 6, …: The 2, 4, 6, … have seniority 2, so the B(E 2: 4+ 2+) is an even tensor ( cause E 2) seniority conserving transition, and hence follows the above rule. We will see an example of this next.

2+