Sample Paths Convergence and Averages Convergence Definition an

Sample Paths, Convergence, and Averages

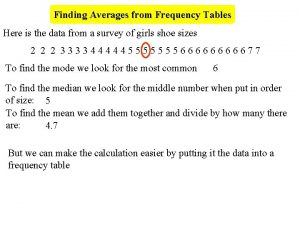
Convergence • Definition: {an : n = 1, 2, …} converges to b as n ∞ means that > 0, n 0( ), such that n > n 0( ), |an – b| < • Example: an = 1/n converges to 0 as n ∞ since > 0, choosing n 0( ) = 1/ ensures that n > n 0( ), an = 1/n < 1/n 0( ) < 2

Convergence Almost Surely (with Probability 1) • {Yn : n = 1, 2, …} converges almost surely to μ as n ∞, if ε > 0, P{limn ∞ |Yn – μ| > ε} = 0 • In other words, the probability mass of the set of sample paths that misbehave (Yn deviates from μ by more than ε) is 0 if we take n to be large enough – Note: This does not mean that no sample path misbehaves, and only that the total probability mass of these “bad” paths is (of measure) zero – A sample path misbehaves if no matter what value of n we choose, it is still possible to have |Yn – μ| > ε Consider the average of n coin flips. Most sample paths will converge to a value of ½. However, some sample paths wont, e. g. , the sample path 1, 1, 1, … We have convergence almost surely, because even though there an uncountable number of “bad” paths, that number becomes vanishingly small (of measure 0) as n goes to infinity 3

Convergence in Probability • Yn : n = 1, 2, …} converges in probability to μ as n ∞, if ε > 0, limn ∞P{|Yn – μ| > ε} = 0 (the limit applies to the probability, and not the random variables) • In other words, the odds that an individual sample path behaves badly for Yn go to 0 as n ∞ – Pick a given n and a random path, what are the odds that it is “bad”? – As n grows, those odds should go to 0 • However, this does not preclude the possibility that all (or a nonnegligible number) sample paths occasionally behave badly as n ∞ • Convergence almost surely implies convergence in probability, but the converse is not true – Example: See review problem S 4. 4 4

Strong & Weak Laws of Large Numbers • Weak Law: Let X 1, X 2, X 3, … be i. i. d. random variables with mean E[X], Sn = Σ{i=1, …, n}Xi, and Yn = Sn/n Then Yn converges in probability to E[X] • Strong Law: Let X 1, X 2, X 3, … be i. i. d. random variables with mean E[X], Sn = Σ{i=1, …, n}Xi, and Yn = Sn/n Then Yn converges almost surely to E[X] • Implications: Almost every sample paths of successive trials of Xn converges to a mean value of E[X] – There can still be bad sample paths, but the odds of picking one tend to zero as n ∞ 5

Time & Ensemble Averages • Basic concept: Run a single experiment for 10 hours versus run 100 experiments of 6 minutes each – Record average value of experiment variable over the 10 hours of the first experiment and compare it to the average of the experiment variable at the end of each of the 100 6 minutes experiments • Time average • Ensemble average where pi = limt ∞P{N(t) = i} 6

System Averages • Average number of jobs in system: N – Time average: In every time interval during which the number of jobs is constant, record interval duration, ti, and number of jobs, ni • Time average of number of jobs is Ntime = (Σi. Niti)/(Σiti) – Ensemble average: Run M experiments of duration t, where Mt = Σiti, and record nk(t), k = 1, 2, …, M • Ensemble average of number of jobs is Nensemble = Σknk(t)/M • Average job time in system 7

Ergodicity • An ergodic system is positive recurrent, aperiodic, and irreducible – Irreducible: We can get from any state to any other state – Positive recurrent: Every system state is visited infinitely often, and the mean time between successive visits is finite (and the visit of each state is a renewal point – the system probabilistically restart itself) – Aperiodic: The system state is not deterministically coupled to a particular time period • For an ergodic system, the ensemble average exists and with probability 1 is equal to the time average 8

Non-Ergodic Systems • Systems where the state evolution depends on some initial conditions – Flip a coin and with probability p the system will receive 1 job/sec, and with probability 1 – p it will receive 2 jobs/sec – System state at time t will be very different depending on the starting condition • Periodic systems – At the start of every 5 mins interval, the system receives 2 jobs each taking 1 min to process – The ensemble average does not exist in this case (different results depending on when the systems are sampled) 9