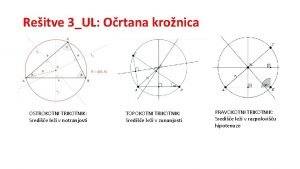
Reitve nalog 1031 Imamo ravno eleznico s postajami

Rešitve nalog

1031 • Imamo ravno železnico s postajami na koordinatah x 1, x 2, …, xn • Cena vozovnice je odvisna od oddaljenosti med postajama (d = |xi – xj|): – – Če je 0 < d ≤ L 1, je cena c 1 Če je L 1 < d ≤ L 2, je cena c 2 Če je L 2 < d ≤ L 3, je cena c 3 Velja c 1 < c 2 < c 3, vse c*, L*, x* so podane • Iščemo najcenejšo skupno ceno za pot od xi do xj • Rešitev: – Recimo, da je i < j; potem ni nobene koristi od tega, da bi šli kdaj v desno, ves čas moramo le v levo – Naj bo f(k) najcenejša pot od i do k: f(k) = min { f(u) + c 3 : xk – L 3 ≤ xu < xk – L 2 }, min { f(u) + c 2 : xk – L 2 ≤ xu < xk – L 1 }, min { f(u) + c 1 : xk – L 1 ≤ xu < xk } } – Ko gledamo vse večje k, počasi premikamo meje med intervali – Za vsak interval lahko vzdržujemo kopico z njegovimi f(u), lahko pa nad tabelo f gradimo binarno drevo, ki ima v vozliščih minimume po poddrevesih

1217 • Gledamo 2 n-mestne nize števk; koliko je takih, kjer: – Je vsota levih n števk enaka vsoti desnih n števk; in hkrati – Je vsota števk na sodih mestih enaka vsoti na lihih mestih • Rešitev: – Naj bo L(x) / D(x) vsota levih/desnih pol števk, Li(x) in So(x) pa vsota števk na levih/desnih pol mestih – Naj bo f(k, u, v) = koliko je 2 k-mestnih nizov x, pri katerih je L(x) – D(x) = u in Li(x) – So(x) = v • Na koncu nas seveda zanima f(n, 0, 0) • u in v gresta od – 9 k do +9 k – Recimo, da x dobimo tako, da vzamemo y in na začetek vrinemo črko a, na konec pa b • Potem je L(x) = L(y) + a, D(x) = D(y) + b, Li(x) = So(y) + a, So(x) = Li(y) + b • Torej u(x) : = L(x) – D(x) = (a – b) + u(y), v(x) : = Li(x) – So(x) = (a – b) – v(y) • Torej f(k, u, v) = Sa, b 0. . 9 f(k – 1, u – (a – b), (a – b) – v)

1221 #. #. # ##. ## #. . . # ##. ## • Imamo karirasto mrežo, vsako polje je črno ali belo • Iščemo največji bel karo v črnem kvadratu Lažji problem: iščimo bel karo ne glede na to, ali je v črnem kvadratu ### ##. . . ## #. . . # ##. . . ## ### – Naj bo a(x, y) velikost največjega belega kara z dnom v (x, y) – a(x, y) = 0, če je to polje črno; sicer je a(x, y) = 1 + min {a(x – 1, y – 1), a(x – 1, y), a(x, y – 1)} • Vrnimo se k prvotnemu problemu: – Naj bo A(x, y) velikost največjega belega kara v črnem kvadratu, z dnom v (x, y) – Preprost razmislek pokaže, da je A(x, y) = a(x, y) ali pa A(x, y) = 0, odvisno od tega, ali so v celoti prisotni vsi štirje črni trikotniki – Črne trikotnike lahko preverjamo na podoben način kot prej bele kare – Lahko pa tudi preštejemo črna polja v kvadratu • b(x, y) = število črnih polj v stolpcu od (x, 0) do (x, y) • B(x, y) = število črnih polj v pravokotniku od (0, 0) do (x, y) • B(x 2, y 2) – B(x 2, y 1 -1) - B(x 1 -1, y 2) + B(x 1 -1, y 1 -1) = število črnih polj v pravokotniku (x 1. . x 2) × (y 1. . y 2).

1238 • Nize bi radi predstavili krajše tako, da ponavljanje podniza predstavimo s številko: cabbbb c 2(a 3(b))b – Iščemo najkrajšo možno takšno predstavitev danega niza • Rešitev: naj bo s 1 s 2…sn naš prvotni niz in f(i, j) naj bo dolžina najkrajša predstavitev podniza si…sj – Lahko znak si predstavimo neposredno in dobimo si + f(i + 1, j) – Če se podniz si…si+d-1 še t-krat ponovi, imamo lahko predstavitev oblike str(t) + “(“ + f(i, i+d-1) + “)” + f(i + td, j) – Med temi možnostmi obdržimo najkrajšo – Kakšen je t v odvisnosti od i in d: • for d : = 1 to n do for i : = 1 to n – d + 1: if s[i…i+d-1] = s[i+d…i+2 d-1] then t(i, d) : = t(i + d, d) + 1 else t(i, d) : = 1; • Da bo primerjanje podnizov bolj učinkovito, si lahko pomagamo s hashiranjem (npr. Rabin-Karpove hash kode)

1244 • Danih je n ≤ 100 kart, i-ta karta tehta mi ≤ miligramov. – Imamo neko podmnožico teh kart s skupno težo M miligramov. – Katere karte so v njej? • To je različica problema 0/1 -nahrbtnika: – Naj bo f(i, m) = ali je mogoče izmed kart {1, …, i} narediti tak izbor, ki ima skupno težo natanko m – Torej f(1, m) = true pri m = m 1 in false drugod – In f(i, m) = f(i – 1, m) or f(i – 1, m – mi) • Če si tudi zapomnimo, katera od gornjih možnosti je pripeljala do rezultata true, bomo lahko na koncu rekonstruirali konkretni izbor kart • Če sta bili obe možnosti true, potem izbor ni enoličen – Na koncu vrnemo f(n, M)

1276 • Imamo n ≤ 40 vagonov, vsak je oblike AA, AB, BA ali BB. – Stakniti jih moramo v niz v poljubnem vrstnem redu, vendar tako, da se prvi znak naslednjega vagona vedno ujema z drugim znakom prejšnjega vagona – Prvi in zadnji znak celega niza sta tudi predpisana – Ali se to sploh dá? • Rešitev: – Če imamo več vagonov iste oblike, jih ni treba ločevati med sabo; dovolj je, če si zapomnimo, koliko jih je – f(x, y, k. AA, k. AB, k. BA, k. BB) = ali se da sestaviti vlak, ki se začne na x, konča na y in vsebuje kuv vagonov oblike uv (za vsako obliko) – Na primer: f(A, v, k. AA, k. AB, k. BA, k. BB) = f(A, v, k. AA – 1, k. AB, k. BA, k. BB) or f(B, v, k. AA, k. AB – 1, k. BA, k. BB) – Če je kakšen od kuv-jev negativen, je odgovor false – Robni primeri: če je kxy = 1 in ostali kuv-ji enaki 0, je f(x’, y’, …) = true pri x = x’, y = y’, sicer false – Podproblemov je največ 2 ∙ 404 10 mio; v resnici še manj, ker nas omejuje začetni razpored vagonov po oblikah

1342 • Imamo n delavnic, ki proizvajajo metle. Delavnica i lahko izdela največ ki metel. Cena j-te metle, izdelane v i, je cij. – V nalogi je cij podana kot linearna funkcija j-ja. • Radi bi izdelali m metel, kako naj jih razporedimo med delavnice, da bo najceneje? • Rešitev: – Naj bo f(i, r) = najnižja cena za za izdelavo r metel z delavnicami 1, 2, …, i. – Potem je f(1, r) = c 11 + c 12 + … + c 1 r. – Pri večjih r se moramo odločiti, koliko metel, recimo s, izdelamo v zadnji delavnici, i : f(i, r) = min { f(i – 1, r – s) + ci 1 + … + cis : 0 ≤ s ≤ min(ki , s) }

1424 • Imamo n ≤ 105 postaj in k ≤ 50000 potnikov, za vsakega i tudi vemo, na kateri postaji si čaka in kam (ei) se hoče peljati – Na avtobusu je hkrati lahko največ m potnikov. – Katere naj poberemo, da bo skupno število prepeljanih potnikov največje? • Rešitev: požrešni algoritem – A : = {} za vsakega potnika i, po naraščajočih časih izstopa: če pri naboru potnikov A naš avtobus kakšen del poti [si , ei) ni polno zaseden, potem A : = A {i} – A : = {} za vsakega potnika i, po naraščajočih časih vstopa: A : = A {i} če je pri tako povečani A avtobus kdaj prepoln, potem pobriši iz A potnika z najkasnejšim časom izstopa;