RATIONAL FUNCTION Rational Function 1 st Quad Definition

RATIONAL FUNCTION

Rational Function (1 st Quad) Definition: A rational function is a function that, when you multiply each “x” and “y” together in a table of values they will equal the same number. The function has the form: where “a” is a constant number

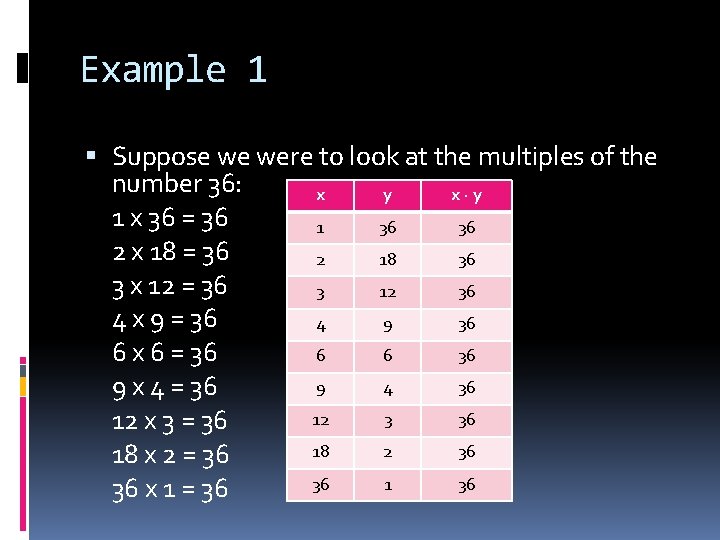
Example 1 Suppose we were to look at the multiples of the number 36: x y x·y 1 x 36 = 36 1 36 36 2 x 18 = 36 2 18 36 3 x 12 = 36 3 12 36 4 x 9 = 36 4 9 36 6 6 36 6 x 6 = 36 9 4 36 9 x 4 = 36 12 3 36 12 x 3 = 36 18 2 36 18 x 2 = 36 36 1 36 36 x 1 = 36

Example 1 (continued) Let’s graph this puppy 40 x y 35 1 36 30 2 18 25 3 12 20 4 9 6 6 9 4 12 3 18 2 36 1 15 10 5 0 0 5 10 15 20 25 Our equation is then 30 35 40

Note: In this course, you will not have to worry about this function being translated up/down/left/right That being said, this means that the x-axis and yaxis are never touched by our curve, EVER! The curve gets closer and closer to both the x & y -axis but will never touch them. Why do you think that is? Let’s look at another example, to make sure we understand this function thoroughly.

Example 2 Suppose this class was given 200 dollars for excellent achievement in mathematics. Would you (as a class) want less students in the class or more students in the class if the money was distributed evenly among each student? Lets look at the situation. . .

Example 2 (continued) In our example; - “x” represents the number of students - “y” represents the amount of money each would receive. Why is this? “y” depends on “x” always so. . . . Amount of $ / student depends on # of students makes sense.

Example 2 (continued) If there was only one student in the class, how much $ would they get? $ 200 because If there were two students in the class, how much would each get? $ 100 because If there were ten students in the class, how much would each get?

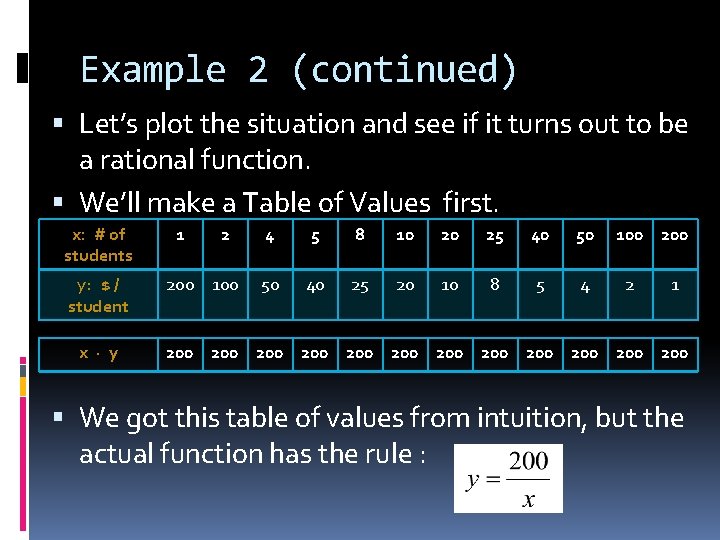
Example 2 (continued) Let’s plot the situation and see if it turns out to be a rational function. We’ll make a Table of Values first. x: # of students y: $ / student x · y 1 2 200 100 4 5 8 10 20 25 40 50 50 40 25 20 10 8 5 4 100 2 1 200 200 200 We got this table of values from intuition, but the actual function has the rule :

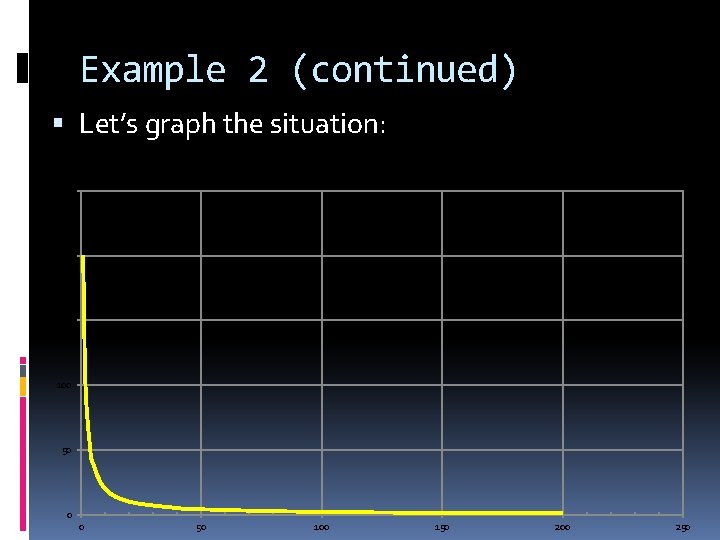
Example 2 (continued) Let’s graph the situation: 250 200 150 100 50 0 0 50 100 150 200 250

Notes We just did two examples where we were dealing with values only in the first quadrant. (since the x and y values could not be negative for those situations) But can our function ever use negative numbers? If the word problem dictates that negative number can be used, then absolutely use them.

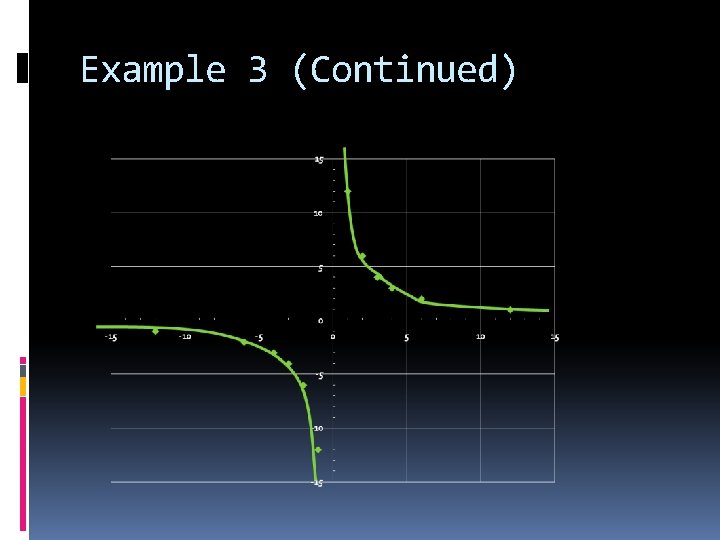
Example 3 Say we had a function and x can be either positive or negative. We would obtain a Table of Values that looks something like this: x -12 -6 -4 -3 -2 -1 1 2 3 4 6 12 y -1 -2 -3 -4 -6 -12 12 6 4 3 2 1 12 12 12 x*y What would this graph look like?

Example 3 (Continued)

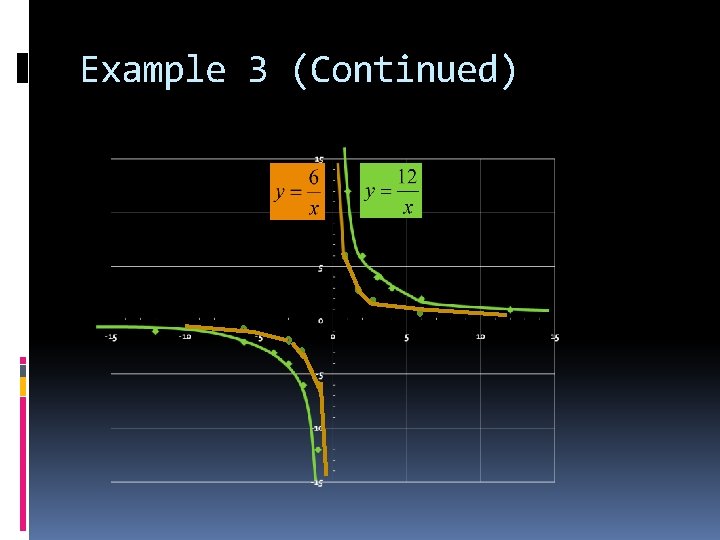
Example 4 Say we had a function and x can be either positive or negative. We would obtain a Table of Values that looks something like this: x -6 -3 -2 -1 1 2 3 6 y -1 -2 -3 -6 6 3 2 1 x*y 6 6 6 6 What would this graph look like compared to the first equation

Example 3 (Continued)

Notes When your curve of the Rational Function goes on both sides of the y-axis (like in the last example) it has a special name: Hyperbola In the function , “a” is just a number. As a increases in value, the less steep the curve becomes (as a increases, the more curve looks like a bunny hill rather than a expert ski run)