Quantum Mechanics 101 5 WaveParticle Duality and the

Quantum Mechanics 101. 5 Wave-Particle Duality and the Wavefunction

Review of Last Time § § Quantum mechanics is AWESOME, but it challenges our physical intuition Light and “particles” behave like waves when traveling and like particles when interacting or being observed Since they propagate like waves, both light and “particles” can produce interference patterns We can describe this duality through the use of a wave function Y(x, t) which describes the (unobserved) propagation through space and time

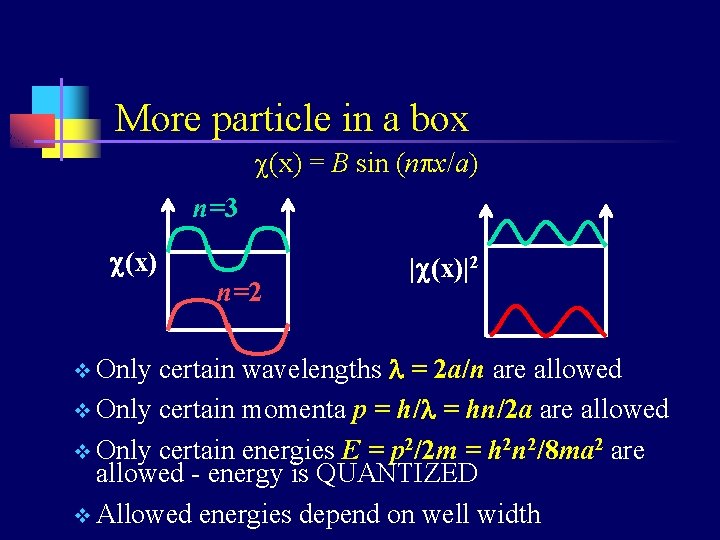
Application: particle in a box v v v If a particle is confined to a region by infinitelyhigh walls, the probability of finding it outside that region is zero. Since nature is generally continuous (no instantaneous changes), the probability of finding it at the edges of the region is zero. The position-dependent solution to the Schrödinger equation for this case has the form of a sine function: c(x) = B sin (npx/a) (a=well width)

More particle in a box c(x) = B sin (npx/a) n=3 c(x) n=2 |c(x)|2 certain wavelengths l = 2 a/n are allowed v Only certain momenta p = h/l = hn/2 a are allowed v Only certain energies E = p 2/2 m = h 2 n 2/8 ma 2 are allowed - energy is QUANTIZED v Allowed energies depend on well width v Only

What about the real world? v v v So confinement yields quantized energies In the real world, infinitely high wells don’t exist Finite wells, however, are quite common Schrödinger equation is slightly more complicated, since Ep is finite outside well Solution has non-trivial form (“trust me”) |c(x)|2 n=1

What about the real world? v v Solution has non-trivial form, but only certain states (integer n) are solutions Each state has one allowed energy, so energy is again quantized Energy depends on well width a Can pick energies for electron by adjusting a |c(x)|2 n=1 x

What have we learned today? § § Integrating the square of the wave function over a region gives us the probability of finding the object in that region A “particle” confined to an infinitely-high box is described by a wave function of a sine. “particles” in finite wells or in atoms are described by more complicated wave functions All three situations result in quantized (only certain values allowed) energies