Quantum Computing Rieffel Polak Chapter 8 Shors Algorithm

Quantum Computing, Rieffel & Polak Chapter 8 Shor’s Algorithm Drs. Charles Tappert and Ron Frank The information presented here, although greatly condensed, comes almost entirely from the textbook

Chapter 8 Shor’s Algorithm n In 1994, inspired by Simon’s algorithm, Shor found a polynomial-time quantum algorithm for factoring integers n n Shor’s algorithm quickly finds the period of a function n n The previous sieve algorithm requires O(exp(m 1/3)) steps The period is then used to factor the given integer The crux of the quantum part of the algorithm is the quantum Fourier transform n The remaining complications are classical, particularly the extraction of the period from the measured value

Chapter 8 Shor’s Algorithm 8. 1 Classical Reduction to Period-Finding n n The order of a mod M = smallest integer r s. t. ar = 1 mod M Consider the function f(k) = ak mod M n n Because ak = ak+r mod M iff ar = 1 mod M, for a relatively prime to M, the order r of a mod M is the period of the function f If ar = 1 mod M and r is even, (ar/2 + 1)(ar/2 - 1) = 0 mod M As long as neither (ar/2 + 1) nor (ar/2 - 1) is a multiple of M, both have a nontrivial common factor with M The above suggests a strategy for factoring M n n Choose a random integer a & determine the period r of f(k) = ak mod M If r is even, compute the gcd of ar/2+1 and M Repeat if necessary Thus, factoring M has been converted to a different hard problem, that of computing the period of the function f(k) = ak mod M (Shor’s alg)

Chapter 8 Shor’s Algorithm 8. 2 Outline of Shor’s Factoring Algorithm 1. 2. 3. 4. 5. 6. Choose a random integer 0<a<M. Are a and M relatively prime? If yes, we found a factor of M, otherwise continue. Use quantum parallelism to compute f(x) = ax mod M on the superposition of inputs. Apply a quantum Fourier transform to the result with n such that M 2 < 2 n < 2 M 2 and m = �log M� (ceiling function) qubits to represent M Perform a quantum measurement. With high probability, a value v close to a multiple of 2 n/r will be obtained. Use classical methods – e. g. , continued fraction expansion – to estimate a period q from the value v. When q is even, use the Euclidean GCD algorithm to check if aq/2 + 1 (or aq/2 - 1) has a nontrivial common factor with M. Repeat all steps if necessary.

Chapter 8 Shor’s Algorithm 8. 2 Continued Fraction Expansion

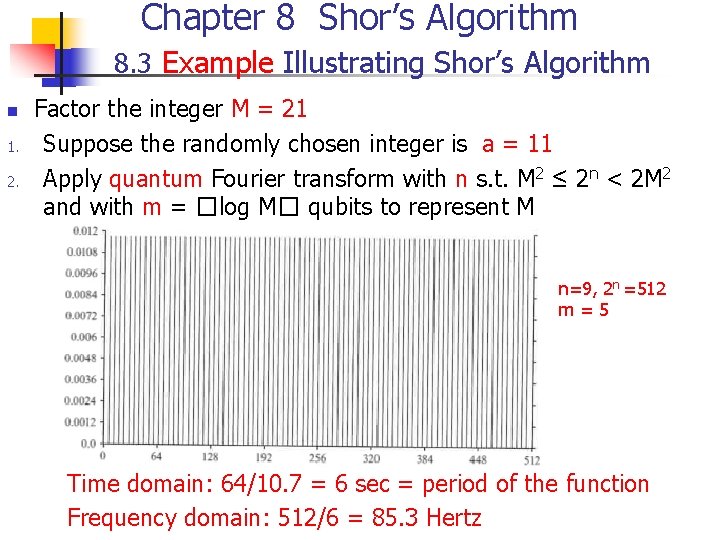
Chapter 8 Shor’s Algorithm 8. 3 Example Illustrating Shor’s Algorithm n 1. 2. Factor the integer M = 21 Suppose the randomly chosen integer is a = 11 Apply quantum Fourier transform with n s. t. M 2 ≤ 2 n < 2 M 2 and with m = �log M� qubits to represent M n=9, 2 n =512 m=5 Time domain: 64/10. 7 = 6 sec = period of the function Frequency domain: 512/6 = 85. 3 Hertz

Chapter 8 Shor’s Algorithm 8. 3 Example Illustrating Shor’s Algorithm n 3. Frequency domain: the quantum measurement v = 427 512/85. 3=6 85. 3 170. 7 341. 3 426. 7

Chapter 8 Shor’s Algorithm 8. 3 Example Illustrating Shor’s Algorithm 1. 2. 3. 4. 5. A a Suppose the quantum measurement returns v = 427 v and 2 n are relatively prime, use continued fraction expansion until the algorithm terminates with 6 = q 2<M<q 3, so q = 6 Since q is even, a 6/2– 1 = 113 -1 = 1330 and a 6/2+1 = 1332 are likely to have a common factor with M. In this example, gcd(21, 1330) = 7 and gcd(21, 1332) = 3