Proof of the Pumping Theorem for Regular Languages

Proof of the Pumping Theorem for Regular Languages Richard Beigel CIS Temple University

The Pumping Theorem for Regular Languages If L is regular then N z such that z L and |z| N u, v, w such that z = uvw , |uv| N, and |v| > 0 i [uviw L]

Proof • Assume L is regular • Then there is a (standardized) DFR P that recognizes L (no EOF or NOOP) • Let be N be the number of control states in P • Let z L and |z| N • Consider P’s accepting computation on input z • Let q 0, q 1, …, qn be the sequence of control states in that computation. Then n N.

Proof • Then there is a standardized DFR P that recognizes L (no EOF or NOOP) • Let be N be the number of control states in P • Let z L and |z| N • Consider P’s accepting computation on input z • Let q 0, q 1, …, qn be the sequence of control states in that computation. Then n N. • By the pigeonhole principle qj=qk for some j<k

Proof • • Let be N be the number of control states in P Let z L and |z| N Consider P’s accepting computation on input z Let q 0, q 1, …, qn be the sequence of control states in that computation. Then n N. • By the pigeonhole principle qj=qk for some j<k • Let u be the string scanned between q 0 and qj

Proof • Let z L and |z| N • Consider P’s accepting computation on input z • Let q 0, q 1, …, qn be the sequence of control states in that computation. Then n N. • By the pigeonhole principle qj=qk for some j<k • Let u be the string scanned between q 0 and qj • Let v be the string scanned between qj and qk

Proof • Consider P’s accepting computation on input z • Let q 0, q 1, …, qn be the sequence of control states in that computation. Then n N. • By the pigeonhole principle qj=qk for some j<k • Let u be the string scanned between q 0 and qj • Let v be the string scanned between qj and qk • Let w be the string scanned between qk and qn

Proof • Let q 0, q 1, …, qn be the sequence of control states in that computation. Then n N. • By the pigeonhole principle qj=qk for some j<k • Let u be the string scanned between q 0 and qj • Let v be the string scanned between qj and qk • Let w be the string scanned between qk and qn • Then uvw = z, |uv| N, |v| 1, • and P accepts uviw for all i 0

Proof • • By the pigeonhole principle qj=qk for some j<k Let u be the string scanned between q 0 and qj Let v be the string scanned between qj and qk Let w be the string scanned between qk and qn Then uvw = z, |uv| N, |v| 1, and P accepts uviw for all i 0 Therefore uviw L for all i 0, completing the proof of the Pumping

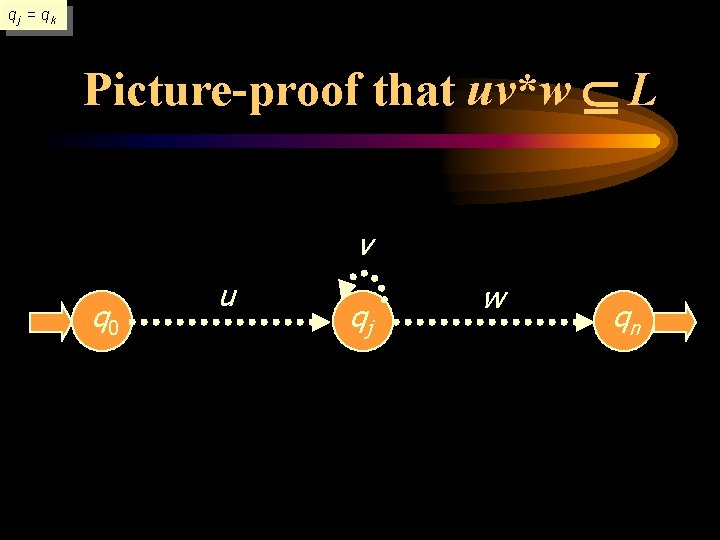
qj = qk Picture-proof that uv*w L v q 0 u qj w qn

Example: L = • • 2 n {a : n 0} Assume L is regular Let N be given by the Pumping Theorem Let z = a. N 2 Let u, v, w be given by the Pumping Theorem Then v = ak where 0 < k N Let i = 2 Then uviw = uv 2 w = uvvw = a. N 2 + k Since N 2 < N 2 + k N 2 + N < N 2 + 2 N + 1 = (N + 1)2, N 2 + k is not a square, so uviw = a. N 2 + k L • This contradicts the Pumping Theorem, so L is not regular

Example: L = • • • m n {a b : m n} Assume L is regular Let N be given by the Pumping Theorem Let z = a. N b. N Let u, v, w be given by the Pumping Theorem Then v = ak where 0 < k N Let i = 2 Then uviw = uvvw = a. N+k b. N Since k > 0, N+k > N, so uviw = a. N+k b. N L This contradicts the Pumping Theorem, so L is not regular

Example: L = • • • m n {a b : m n} Assume L is regular Let N be given by the Pumping Theorem Let z = a. N b. N Let u, v, w be given by the Pumping Theorem Then v = ak where 0 < k N Let i = 0 Then uviw = uw = a. N-k b. N Since k > 0, N-k < N, so uviw = a. N-k b. N L This contradicts the Pumping Theorem, so L is not regular