Online Multicast with Egalitarian Cost Sharing Moses Charikar

Online Multicast with Egalitarian Cost Sharing Moses Charikar (Princeton) Howard Karloff (AT&T) Claire Mathieu (Brown) Seffi Naor (Technion) Mike Saks (Rutgers) Talk presented by Warren Schudy (Brown)

Introduction Multicast: n terminal vertices must connect to root vertex r via paths. Edges have costs c(e). Goal is to minimize total cost: OPT Steiner Tree. Egalitarian cost sharing: an edge e used by the paths of n(e) terminals charges each terminal c(e)/n(e). Terminals are selfish, non-cooperative. Nash equilibrium (N. E. ): no terminal wants to change its path if everything else stays the same. Question: how much more costly is the outcome of selfish choices? That is: bound (cost of N. E. )/ OPT?

Impact of selfishness (cost of worst N. E. )/OPT = n [Koutsoupias Papadimitriou‘ 99] Price of anarchy (cost of best N. E. )/OPT = O(log n/ loglog n) [Anshelevich Dasgupta Kleinberg Tardos Wexler Roughgarden ‘ 04, Agarwal Charikarr ‘ 06] Price of stability Question: what about (cost of N. E. )/OPT for N. E. reachable by some process? Best response dynamics: when activated, a terminal always chooses its current cheapest path to root In which order do activations occur?

Two phase model Activation model [Chekuri Chuzhoy Lewin-Eytan Naor Orda ‘ 06] Phase 1: Terminals are activated one by one Phase 2: Re-activated terminals may change their path (arbitrary sequence of re-activations) Phase 1 r Phase 2 t 4 t 1 t 3 re-fires t 2 2 Ω(log n/ loglog n)≤ (cost of resulting N. E. )/OPT≤ O(√n log n)[CCLNO] r

New results For two phase model: Ω(log n) ≤ (cost of resulting N. E. )/OPT ≤ O(log 3 n) For General sequence of interleaved activations and re-activations, except that terminal arrivals (first activations) are in random order: (cost of resulting N. E. )/OPT = O(√n polylog(n)) Next 5 slides: proof sketch of O(log 3 n) result

Proving 3 O(log n) Potential function cost ≤ ≤ H(n)*cost Re-activations decrease So, cost after phase 2 phase 1 after phase 1 ≤ ≤ after ≤ O(log n)*cost Must prove: (cost after phase 1)≤ O(log 2 n)*OPT

Analysis of phase 1 1. Define “Gap revealing” linear program (cost after phase 1) ≤ Value(LP) 2. Relax the LP and write dual linear program Value(LP) ≤ Value(Dual) by linear programming duality 3. Define feasible dual solution… Value(Dual) ≤ Value(solution) 4. … of value O(log 2 n) OPT Value(solution) =

Gap revealing LP s(i): cost of i’s path on arrival of i cost of new edges bought by i b(i): b(i) =(Cost after phase 1) = b(i)’s s(i) = If terminal j arrives after terminal i, then j could go to i and reuse i’s path with discount: s(j)≤ d(j, i)+s(i)-b(i)/2

Relax, take dual Take a tree T over the terminals, such that children arrive after their parent. Relax the linear program by writing the constraint s(j)≤ d(j, i)+s(i)-b(i)/2 for j child of i in T only So, dual has one variable z(j) for each edge of T between j and parent(j) (C(i): children of i in T)

How is T defined? Must have: children arrive after their parent Take Eulerian tour π of min spanning tree of terminals. Note: Cost(π) ≤ 2(OPT Steiner tree) Try to have: parent(j) is in the vicinity of j along π, and so: d(j, parent(j))=O(log 2 n)* Cost(π) Left subtree r Path to root t 1 t 2 t 4 Right subtree t 3

Random Arrivals Result O(√n polylog(n)) proof sketch Arbitrary interleaving of arrivals and reactivations, but: assume order of arrivals is random Analyze potential Φ Reactivations decrease potential Φ(k): potential right after kth terminal arrives; bound E[Φ(k+1) - Φ(k) given Φ(k)]

Analysis: arrival of j Path picked by j is difficult to analyze. Instead, Consider again Eulerian tour π of min spanning tree of terminals. Pick i randomly from previously arrived terminals in the vicinity of j along π. Connect j to i and follow i’s path.

Conclusion and Open Problems General theme: Bound cost of solutions reachable by best response dynamics Obvious open question: analyze arbitrary mix of arrivals and reactivations Random slow arrivals: Arrivals in random order + arbitrary interleavings When new terminal arrives, solution in equilibrium Other problems ? Multiple source-sink pairs: linear lower bound

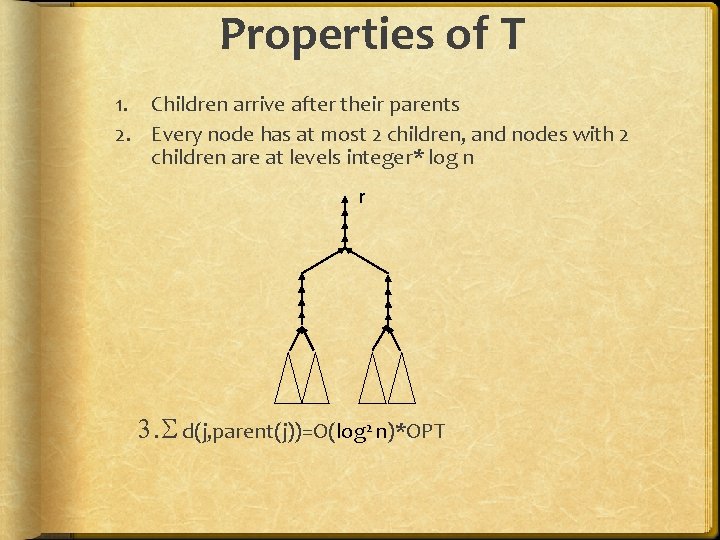
Properties of T 1. Children arrive after their parents 2. Every node has at most 2 children, and nodes with 2 children are at levels integer* log n r 3. d(j, parent(j))=O(log 2 n)*OPT