One Dimensional NonHomogeneous Conduction Equation P M V








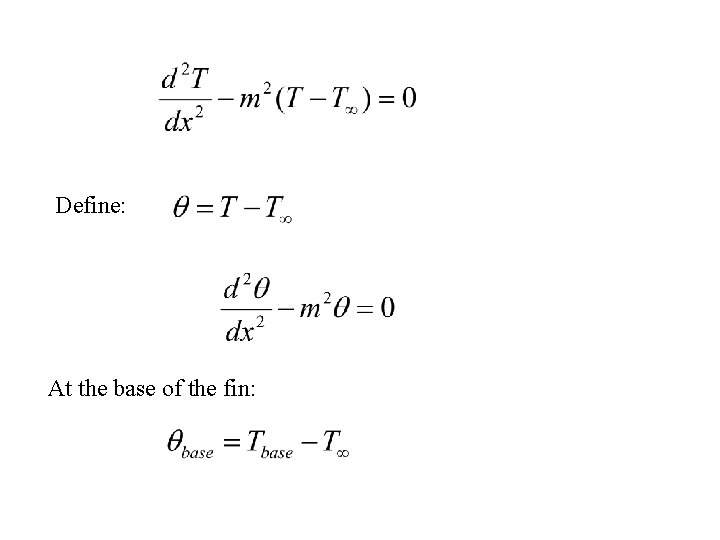


- Slides: 17

One Dimensional Non-Homogeneous Conduction Equation P M V Subbarao Associate Professor Mechanical Engineering Department IIT Delhi Another simple Mathematical modification…. . But finds innumerable number of Applications….

Homogeneous ODE • How to obtain a non-homogeneous ODE for one dimensional Steady State Heat Conduction problems? • Blending of Convection or radiation effects into Conduction model. • Generation of Thermal Energy in a solid body. • GARDNER-MURRAY Ideas.

Nature know More Mathematics !!!

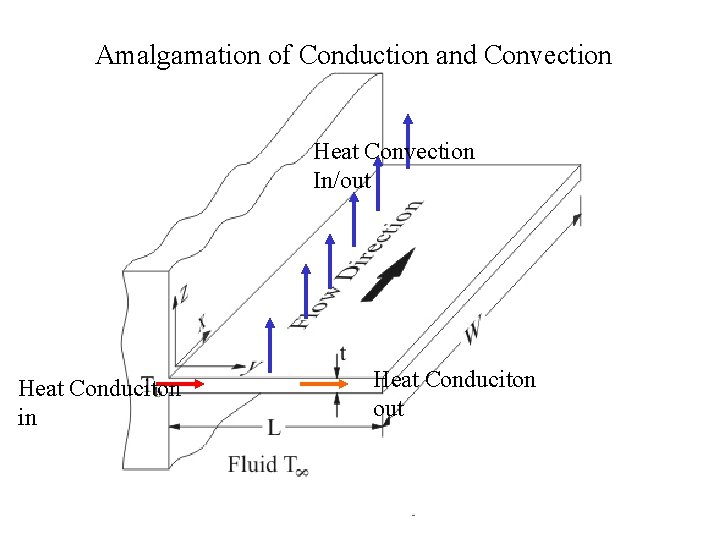
Amalgamation of Conduction and Convection Heat Convection In/out Heat Conduciton in Heat Conduciton out

Innovative Fin Designs

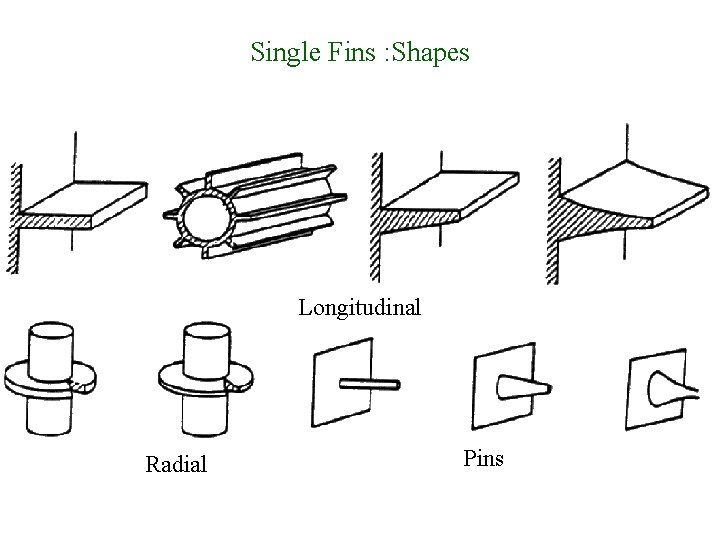
Single Fins : Shapes Longitudinal Radial Pins

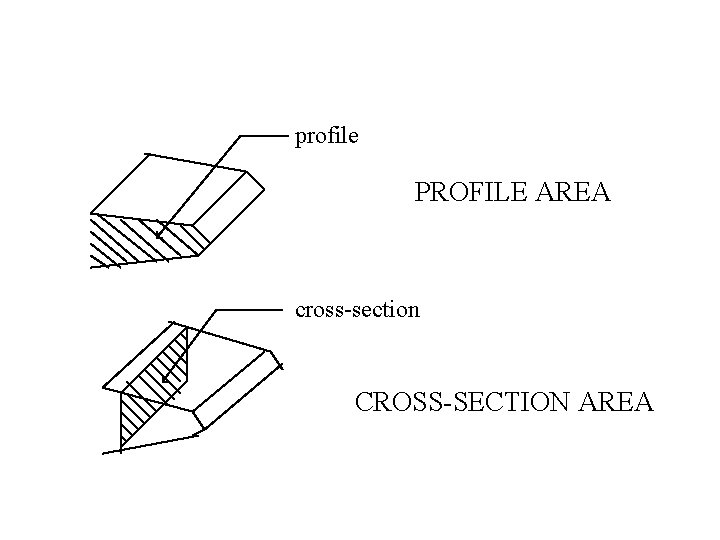
profile PROFILE AREA cross-section CROSS-SECTION AREA

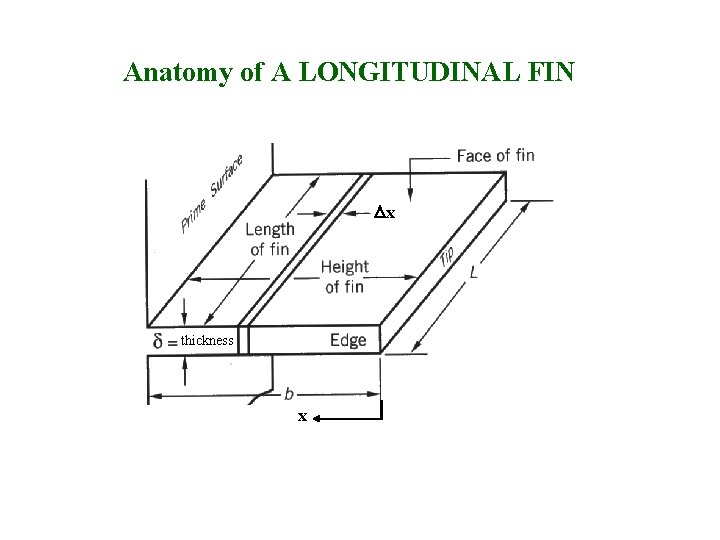
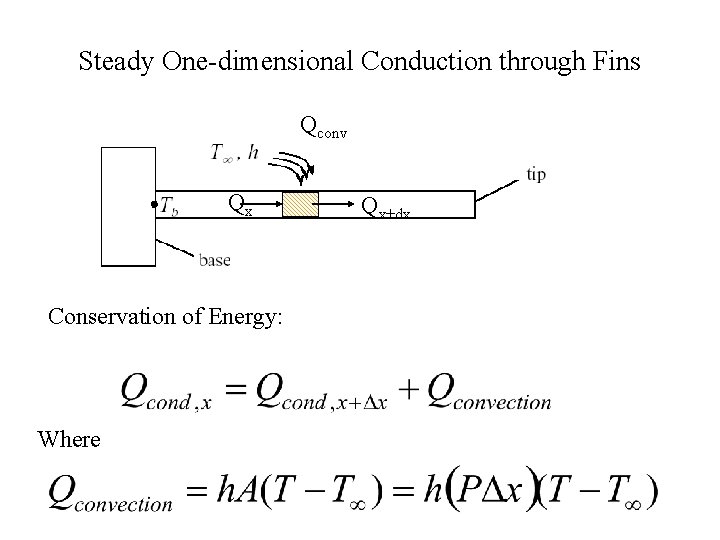
Anatomy of A LONGITUDINAL FIN Dx thickness x

Heat Transfer from Extended Surfaces • Involves conduction through a solid medium as well as convection and/or radiation energy transfer • Goal is to enhance heat transfer between a solid and a fluid. • Possibilities: • increase heat transfer coefficient • increase surface temperature • decrease fluid temperature • increase surface area • The most common way to enhance heat transfer is by increasing the surface area for convection via an extension from a solid medium: fins

GARDNER-MURRAY ANALYSIS ASSUMPTIONS 1. Steady state one dimensional conduction Model. 2. No Heat sources or sinks within the fin. 3. Thermal conductivity constant and uniform in all directions. 4. Heat transfer coefficient constant and uniform over fin faces. 5. Surrounding temperature constant and uniform. 6. Base temperature constant and uniform over fin base. 7. Fin width much smaller than fin height. 8. No heat flow from fin tip. 9. No bond resistance between fin base and prime surface. 10. Heat flow off fin proportional to temperature excess.

Slender Fins Dx thickness x

Steady One-dimensional Conduction through Fins Qconv Qx Conservation of Energy: Where Qx+dx

Substituting and dividing by Dx: Taking limit Dx tends to zero and using the definition of derivative: Substitute Fourier’s Law of Conduction:

For a constant cross section area:
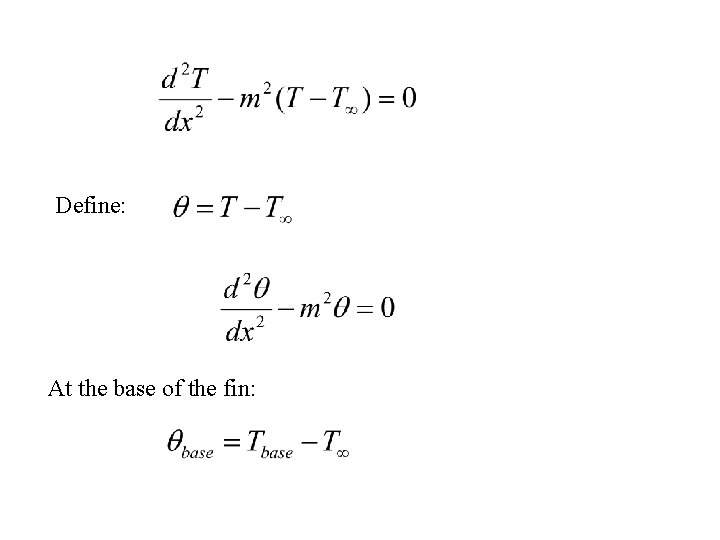
Define: At the base of the fin:

Tip of A Fin
