Neural Nets Something you can use and something

Neural Nets: Something you can use and something to think about Cris Koutsougeras • What are Neural Nets • What are they good for • Pointers to some models and formulations • Methods that you can use • Fun and open issues

What are they good for System of interest (Black box) If I have a finite set of observations (samples) of input-output behavior, can I figure out what function the box performs? • System identification • Prediction-forecasting • Controls, Autogenerate a simulator • Dealing with cases where only samples are known about the function of interest

Why Neural Nets • Target function is unknown except from samples • Target is known but is very hard to describe in finite terms (e. g. closed form expression) • Target function is non-deterministic Something to think about

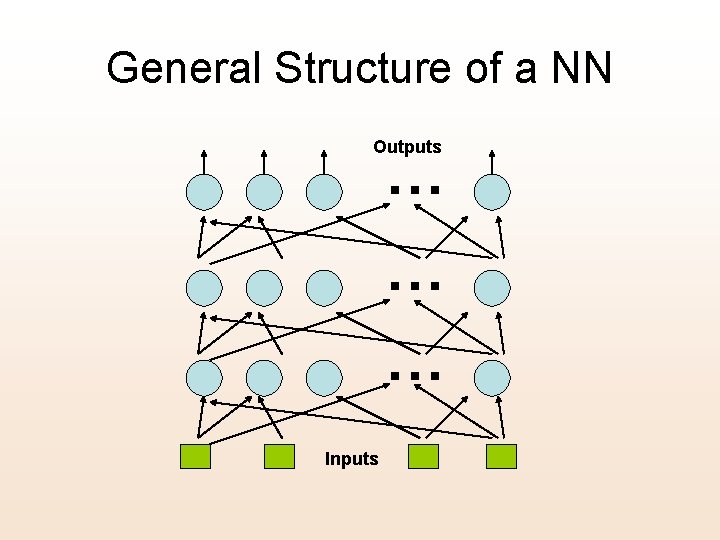
General Structure of a NN Outputs … … … Inputs

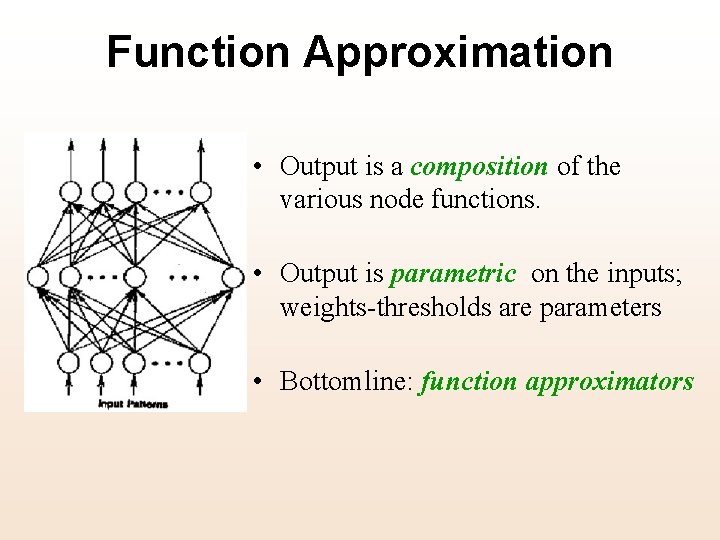
Function Approximation • Output is a composition of the various node functions. • Output is parametric on the inputs; weights-thresholds are parameters • Bottomline: function approximators

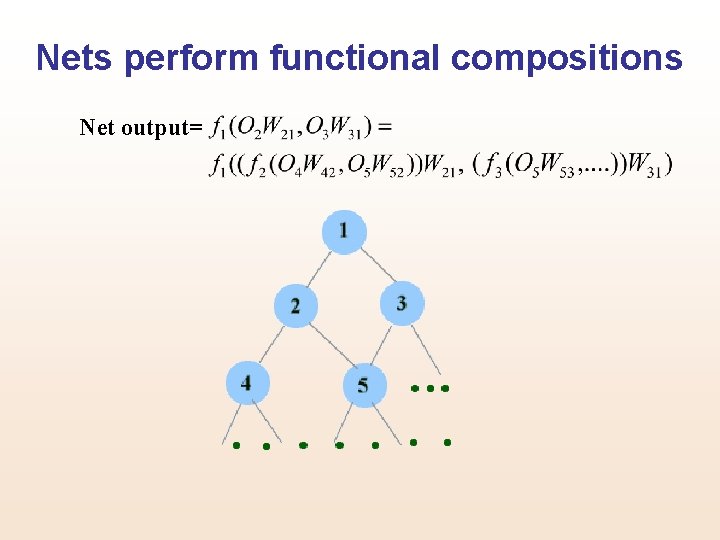
Nets perform functional compositions Net output=

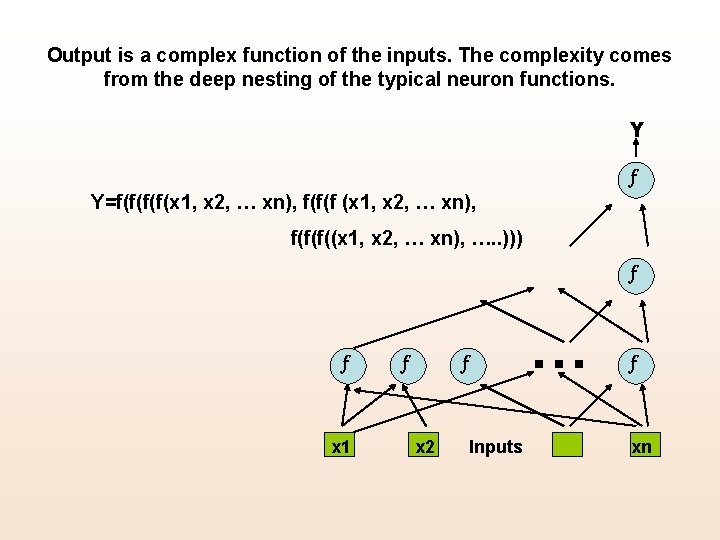
Output is a complex function of the inputs. The complexity comes from the deep nesting of the typical neuron functions. Y f Y=f(f(x 1, x 2, … xn), f(f(f((x 1, x 2, … xn), …. . ))) f f x 1 f … f x 2 Inputs f xn

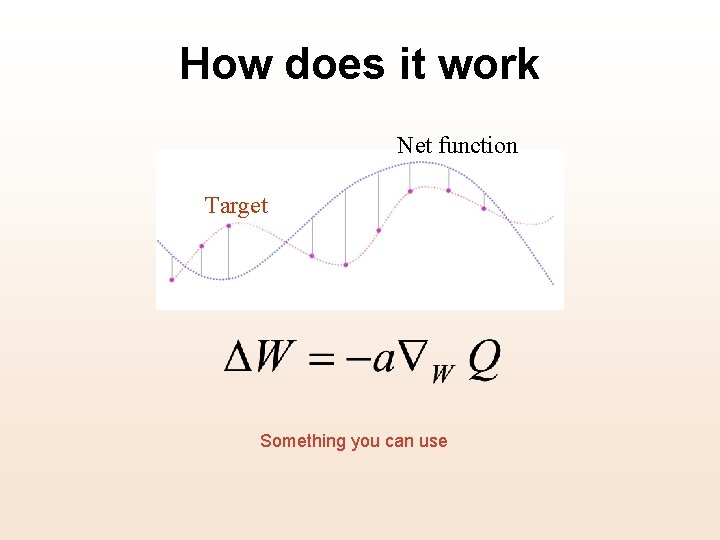
Net’s function is an “elastic” curve By adjusting the weights (curve parameters) the curve fits the samples Adjusting the weights is the key issue

How does it work • We have a Sample set Si={(x 1, t 1), (x 2, t 2), …(xn, tn)} • We have the net producing: yi=f(xi, W) • We define a Quality measure Q(W) that involves f and the targets ti. • We adjust W iteratively: W=-a w Q until Q is optimized. • A convenient Q is usually the mean square error

How does it work Net function Target Something you can use

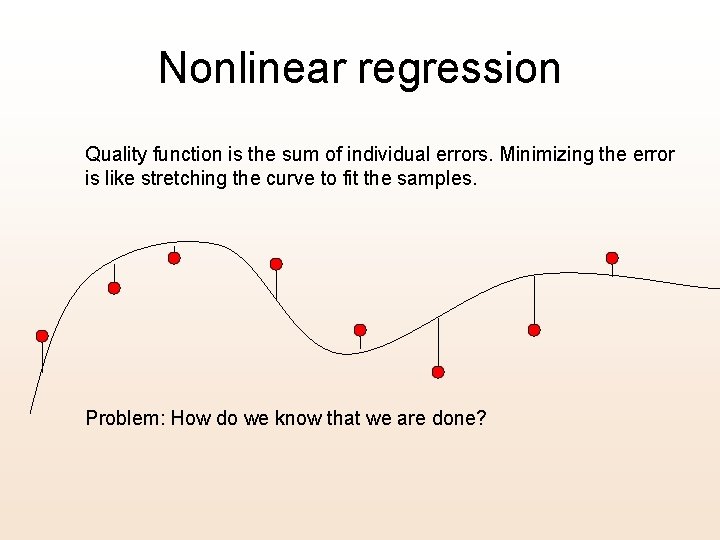
Nonlinear regression Quality function is the sum of individual errors. Minimizing the error is like stretching the curve to fit the samples. Problem: How do we know that we are done?

Nonlinear regression

Nonlinear regression

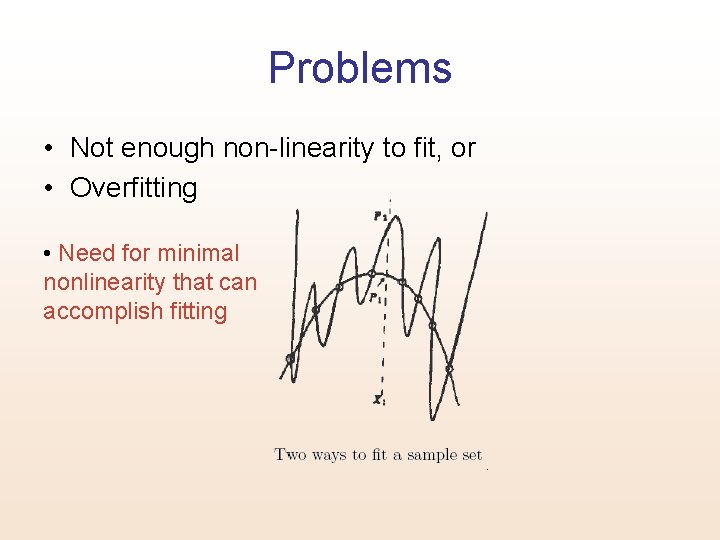
Problems • Not enough non-linearity to fit, or • Overfitting • Need for minimal nonlinearity that can accomplish fitting

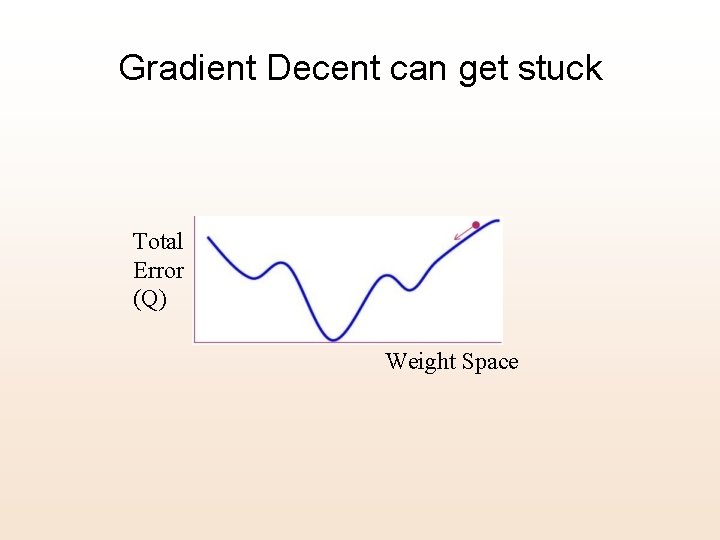
Gradient Decent can get stuck Total Error (Q) Weight Space

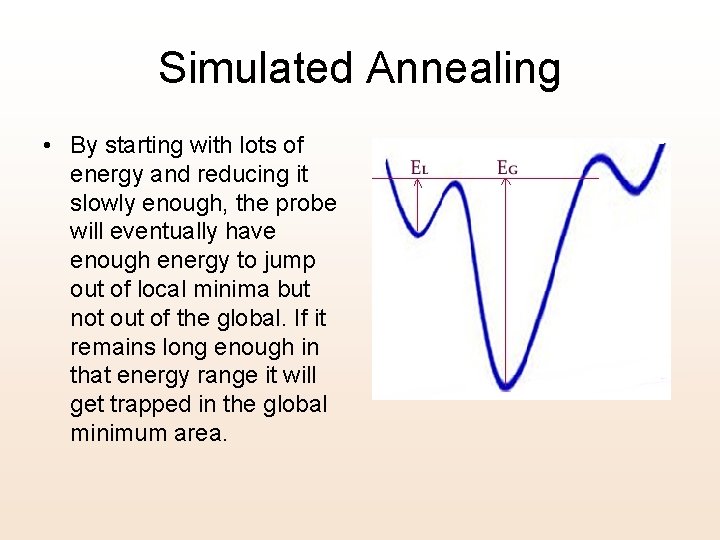
Simulated Annealing Turn a into a time function; start with very large values and gradually reduce it Theorem: If a is reduced at a slow enough rate the probability of landing at the global minimum asymptotically tends to 1 Something you can use

Simulated Annealing • By starting with lots of energy and reducing it slowly enough, the probe will eventually have enough energy to jump out of local minima but not out of the global. If it remains long enough in that energy range it will get trapped in the global minimum area.

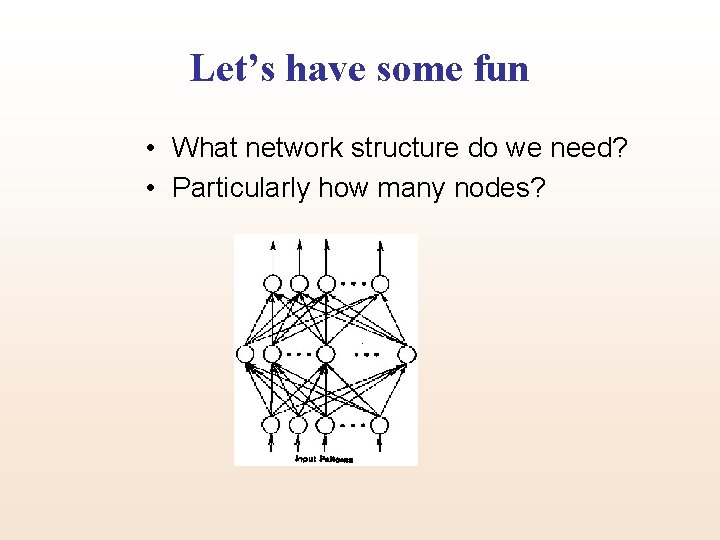
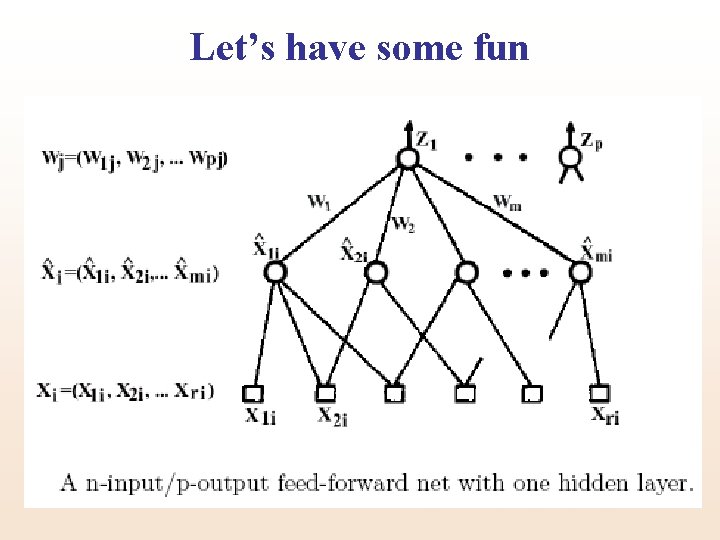
Let’s have some fun • What network structure do we need? • Particularly how many nodes?

Let’s have some fun

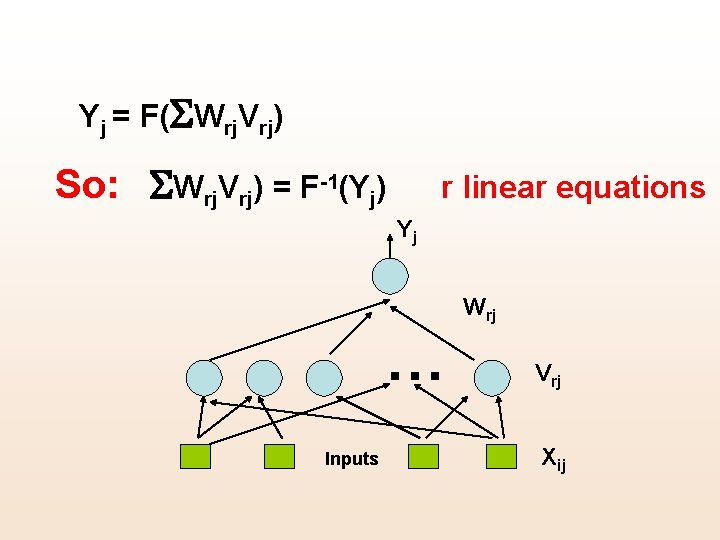
Yj = F(SWrj. Vrj) So: SWrj. Vrj) = F-1(Yj) r linear equations Yj Wrj … Inputs Vrj Xij

Our Framework

New Class of Training Algorithms • We conclude that after proper training (by any method) all intermediate normalized vectors Y project at the same point in the direction of W. • Thus all Y’s are aligned on a plane that is perpendicular to W • New class of algorithms: – Find weights for hidden layer that align all Y’s on a plane – W for the output layer is the normal to that plane

One such Algorithm W di Yi Minimize which is parametric on all weights. Thus use as quality function : and perform a gradient descent: Something you can use

Open Questions: • What is the minimum number of neurons needed? • What is the minimum nontrivial rank that the system can assume? This determines the number of neurons in the intermediate layer.

Interesting Results • The local activation functions must be nonlinear for hidden layer but not for the output layer. We thus arrive at the same result as Kolmogorov’s theorem • The solvability of one necessary hidden layer proves universal approximation with only • The minimum nontrivial rank of the matrix provides the number of hidden layer neurons necessary for proper fitting • Problem: the matrix is parametric and we have no effective method for computing the lowest (non trivial) rank • We came up with other characterizations based on Vapnik. Chervonenkis dimension and PAC learning • However, the problem of a precise optimum number for the hidden layer is at large still open (Something to think about)

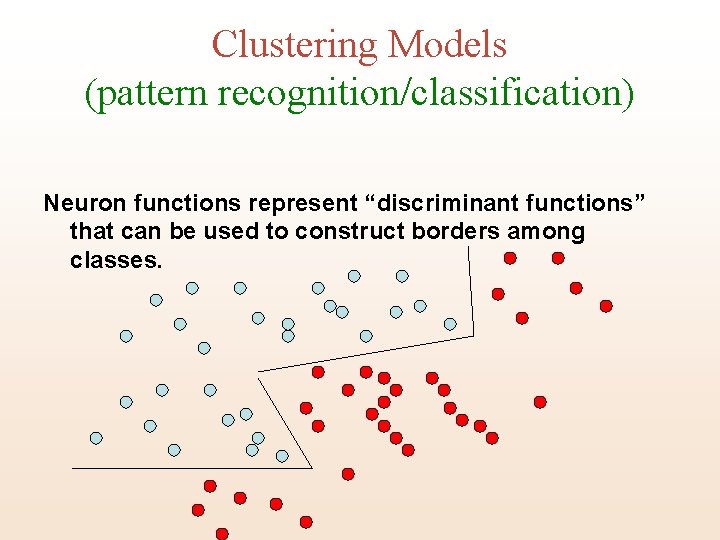
Clustering Models (pattern recognition/classification) Neuron functions represent “discriminant functions” that can be used to construct borders among classes.

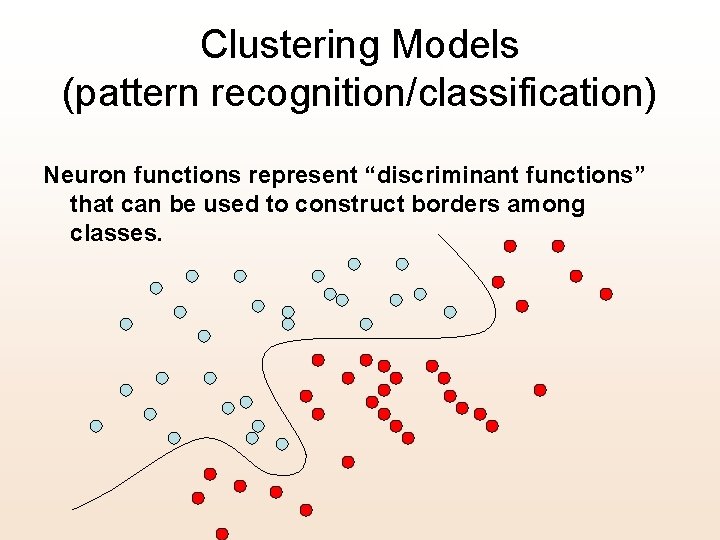
Clustering Models (pattern recognition/classification) Neuron functions represent “discriminant functions” that can be used to construct borders among classes.

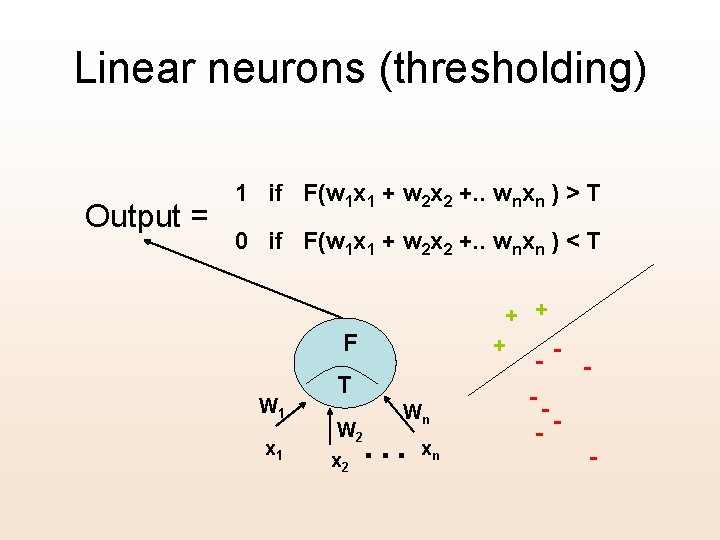
Linear neurons (thresholding) Output = 1 if F(w 1 x 1 + w 2 x 2 +. . wnxn ) > T 0 if F(w 1 x 1 + w 2 x 2 +. . wnxn ) < T + + F W 1 x 1 + T Wn . . . W 2 xn - - -- -

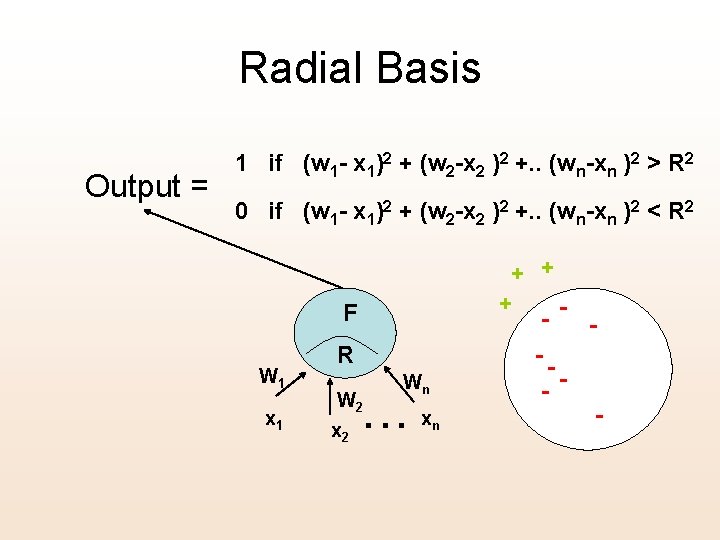
Radial Basis Output = 1 if (w 1 - x 1)2 + (w 2 -x 2 )2 +. . (wn-xn )2 > R 2 0 if (w 1 - x 1)2 + (w 2 -x 2 )2 +. . (wn-xn )2 < R 2 + + + F W 1 x 1 R Wn . . . W 2 xn - - -- -