Moti rotatori Definizioni delle grandezze rotazionali Moto di

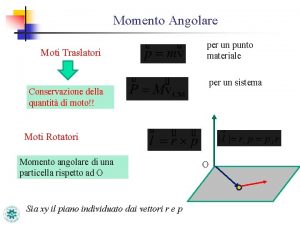
Moti rotatori Definizioni delle grandezze rotazionali

Moto di un corpo rigido • Un corpo rigido può apparire un moto complesso (vedi la clava di un giocoliere). • Ma la complessità di qualunque moto si può semplificare combinando il moto lineare ed il moto rotatorio. • Il moto lineare è il moto del baricentro del corpo, mentre il moto rotatorio è il moto attorno al baricentro del corpo. • Nei moti traslatori tutti i punti di un corpo hanno la stessa velocità lineare • Nei moti rotatori tutti i punti hanno la stessa velocità angolare. • Le velocità lineari dei punti di un corpo in rotazione sono diverse per distanze diverse dall’asse di rotazione.

Moto puramente rotatorio • In un moto puramente rotatorio, tutti i punti di un corpo si muovono di moto circolare w intorno all’ asse di rotazione. • Le velocità tangenziali dei punti di un corpo in rotazione dipendono dalla distanza che hanno rispetto all’asse. Più grande è la distanza di un punto dall’asse di rotazione più grande è la velocità tangenziale. v 1 v 2 v 3 w

Posizione angolare • Per determinare la posizione angolare, serve definire un sistema di riferimento e una unità di misura. • Se un corpo rigido ruota attorno ad un asse, ogni punto i percorrerà una circonferenza di raggio ri diversa da punto. • Quando il punto di un corpo rigido che ruoti attorno ad un asse avrà percorso una distanza s possiamo dire che avrà percorso un angolo q = s/r, rapporto fra la distanza s percorsa sulla circonferenza e il suo raggio r • Un angolo giro è pari a 2 p, un angolo piatto è pari a p ed un angolo retto sarà pari a p/2 • In generale 1 (rad) = 57, 3248° o 1° = 0, 01744 rad

Spostamento e velocità angolare • Dq = q 2 - q 1 è lo spostamento angolare e può essere positivo o negativo. E’positivo se il corpo ruota in senso antiorario, negativo nel caso opposto. • La velocità angolare media è: • La velocità angolare istantanea è: • L’accelerazione angolare istantanea è: o y t en im e s As di r ife r s r x

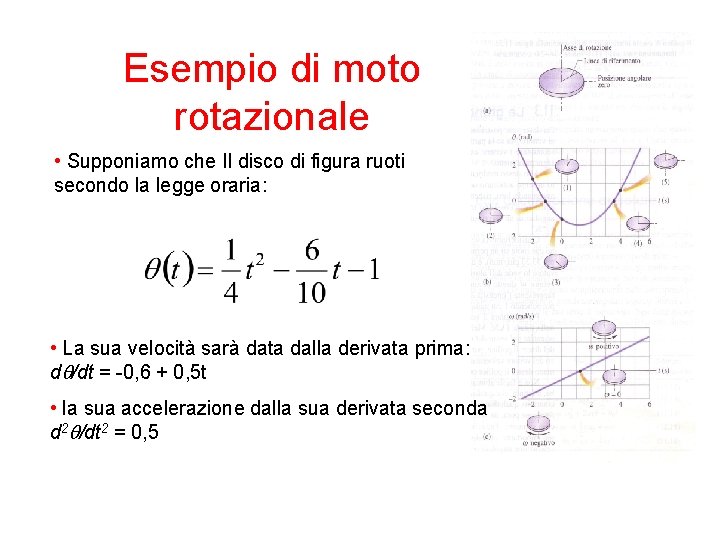
Esempio di moto rotazionale • Supponiamo che Il disco di figura ruoti secondo la legge oraria: • La sua velocità sarà data dalla derivata prima: dq/dt = -0, 6 + 0, 5 t • la sua accelerazione dalla sua derivata seconda d 2 q/dt 2 = 0, 5

Moti rotatori e moti lineari caso dei moti ad accelerazione costante • I moti rotatori sono governati da equazioni omomorfe (simili nella forma), alle equazioni dei moti lineari. v = v 0 + at w = w 0 + a t x-x 0 = v 0 t + ½ at 2 q - q 0 = w 0 t + ½ a t 2 v 2= v 02+2 a(x-x 0) w 2 = w 02 + 2 a(q-q 0) x-x 0 = ½ (v 0+v)t q - q 0 = ½ (w 0 + w)t x-x 0 = vt - ½ at 2 q – q 0 = wt - ½ a t 2

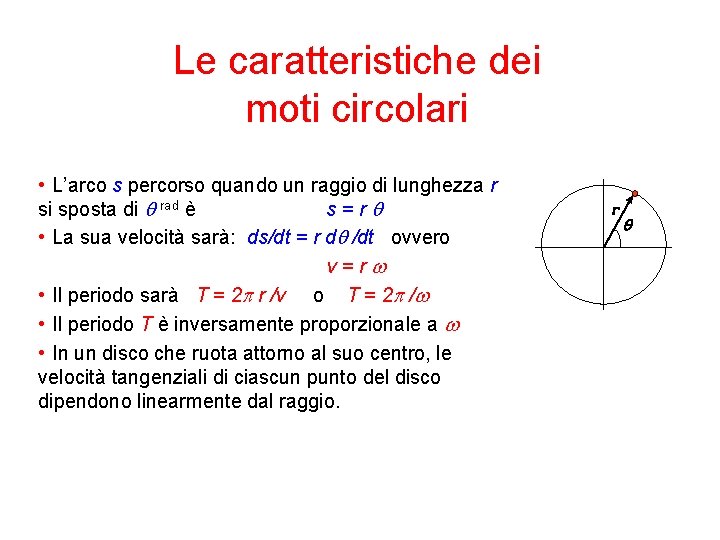
Le caratteristiche dei moti circolari • L’arco s percorso quando un raggio di lunghezza r si sposta di q rad è s=rq • La sua velocità sarà: ds/dt = r dq /dt ovvero v=rw • Il periodo sarà T = 2 p r /v o T = 2 p /w • Il periodo T è inversamente proporzionale a w • In un disco che ruota attorno al suo centro, le velocità tangenziali di ciascun punto del disco dipendono linearmente dal raggio. r q

Moto circolare uniforme • Il moto è circolare perché la sua traiettoria è una circonferenza, ed è uniforme perché il modulo della sua velocità è costante. • E’ costante solo il modulo; non il vettore velocità. • Istante per istante, la velocità, cambia direzione, quindi la velocità varia nel tempo e per questo il moto è soggetto ad una accelerazione. • Il modulo di questa accelerazione sarà: a = v 2/r • la direzione, istante per istante, è perpendicolare al vettore velocità • e il verso diretto al centro della traiettoria Dv v 2 v 1 r 2 r 1 Ds Ricordando un teorema dei triangoli simili v 1

Il moto della Luna • ar v T