Minimum spanning trees Kruskals algorithm Prims algorithm March

Minimum spanning trees Kruskal's algorithm Prim's algorithm March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 1

Kruskal's algorithm for minimum spanning trees • March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 2

Kruskal's algorithm Data types for implementation • We need ADTs that support our required operations efficiently • How do we find the minimum weight edge? – Priority queue! • How can we check for cycles and perform union? – Disjoint sets! March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 3

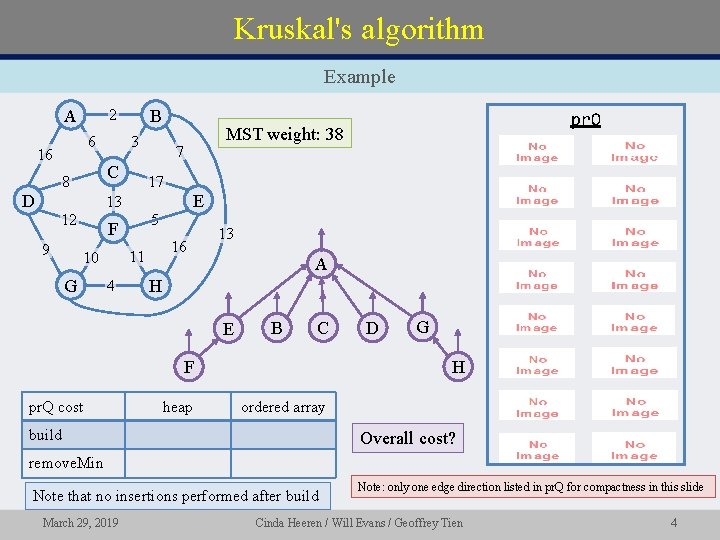
Kruskal's algorithm Example A B 2 6 16 3 C 8 D 7 17 E 13 12 9 5 F G 16 11 10 4 13 A H E B C F pr. Q cost pr. Q MST weight: 38 heap D G H ordered array build Overall cost? remove. Min Note that no insertions performed after build March 29, 2019 Note: only one edge direction listed in pr. Q for compactness in this slide Cinda Heeren / Will Evans / Geoffrey Tien 4

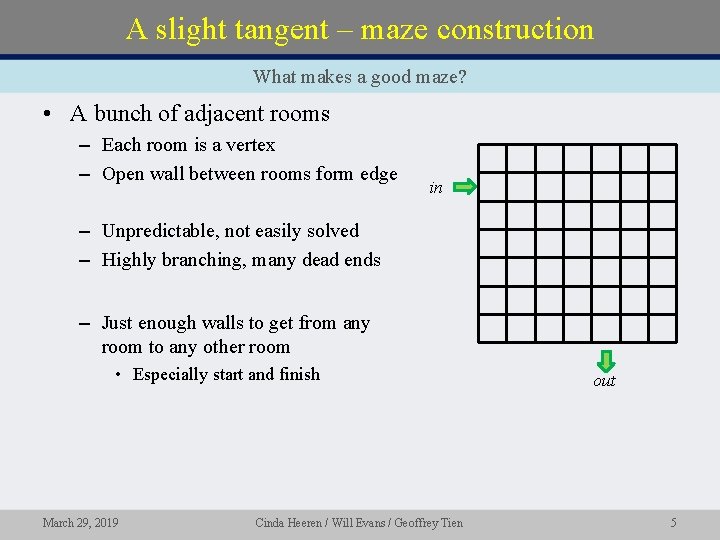
A slight tangent – maze construction What makes a good maze? • A bunch of adjacent rooms – Each room is a vertex – Open wall between rooms form edge in – Unpredictable, not easily solved – Highly branching, many dead ends – Just enough walls to get from any room to any other room • Especially start and finish March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien out 5

Maze under construction • So far, a number of walls have been knocked down, while others remain • Now we consider the wall between rooms A and B – Should we knock it down? • If A and B are otherwise connected • If A and B are not otherwise connected A B This is a lot like Kruskal's algorithm! Solve it using disjoint sets and random edge selection March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 6

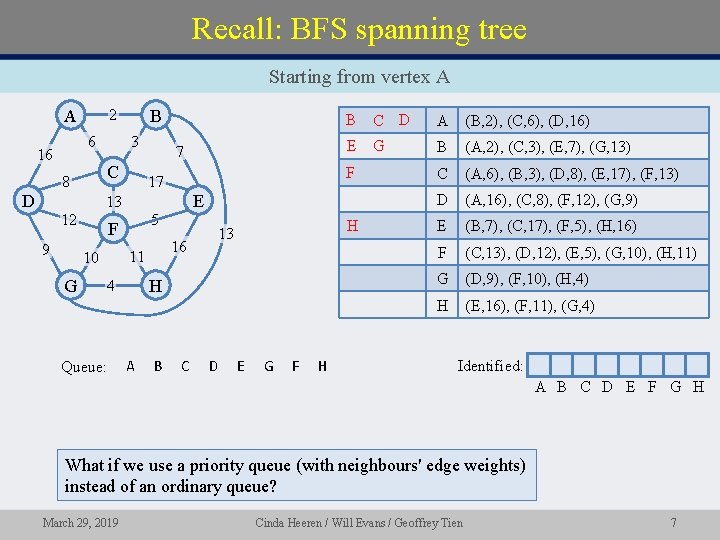
Recall: BFS spanning tree Starting from vertex A A 6 16 B 2 3 C 8 D 9 G G B (A, 2), (C, 3), (E, 7), (G, 13) C (A, 6), (B, 3), (D, 8), (E, 17), (F, 13) D (A, 16), (C, 8), (F, 12), (G, 9) E (B, 7), (C, 17), (F, 5), (H, 16) F (C, 13), (D, 12), (E, 5), (G, 10), (H, 11) G (D, 9), (F, 10), (H, 4) H (E, 16), (F, 11), (G, 4) E 5 H 13 16 11 H 4 Queue: (B, 2), (C, 6), (D, 16) F 17 F 10 A E 7 13 12 B C D A B C D E G F H Identified: T T T T A B C D E F G H What if we use a priority queue (with neighbours' edge weights) instead of an ordinary queue? March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 7

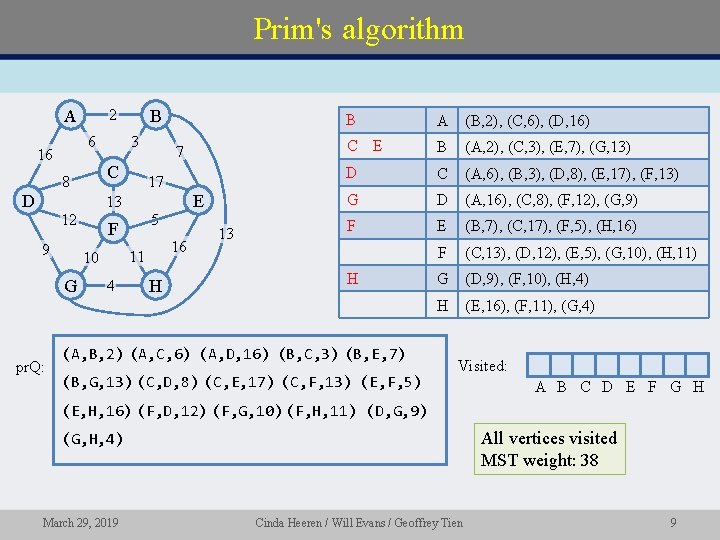
Prim's algorithm • Greedy algorithm • Builds a spanning tree from initially one vertex. • Repeatedly chooses the minimum-weight edge from a vertex in the tree, to a vertex outside the tree – adds that vertex to the tree Prims. Algorithm(v) { mark v as visited, add v to spanning tree while (graph has unvisited vertices) { Find least cost edge (w, u) from a visited vertex w to unvisited vertex u Mark u as visited Add vertex u and edge (w, u) to the minimum spanning tree } } March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 8

Prim's algorithm A 6 16 B 2 3 C 8 D 7 17 E 13 12 9 pr. Q: 16 11 10 G 5 F 4 H 13 B A (B, 2), (C, 6), (D, 16) C E B (A, 2), (C, 3), (E, 7), (G, 13) D C (A, 6), (B, 3), (D, 8), (E, 17), (F, 13) G D (A, 16), (C, 8), (F, 12), (G, 9) F E (B, 7), (C, 17), (F, 5), (H, 16) F (C, 13), (D, 12), (E, 5), (G, 10), (H, 11) G (D, 9), (F, 10), (H, 4) H (E, 16), (F, 11), (G, 4) H (A, B, 2) (A, C, 6) (A, D, 16) (B, C, 3) (B, E, 7) (B, G, 13) (C, D, 8) (C, E, 17) (C, F, 13) (E, F, 5) Visited: T T T T A B C D E F G H (E, H, 16) (F, D, 12) (F, G, 10) (F, H, 11) (D, G, 9) All vertices visited MST weight: 38 (G, H, 4) March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 9

Prim's algorithm Complexity • Actually we can describe Kruskal's algorithm the same way March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 10

Readings for this lesson • Carrano & Henry – Chapters 20. 4. 2 – 20. 4. 3 (Spanning trees, minimum spanning trees) • Next class: – Carrano & Henry, Chapter 20. 4. 4 (Shortest path) March 29, 2019 Cinda Heeren / Will Evans / Geoffrey Tien 11