Maximal Unitarity at Two Loops David A Kosower

Maximal Unitarity at Two Loops David A. Kosower Institut de Physique Théorique, CEA–Saclay work with Kasper Larsen & Henrik Johansson; & work of Simon Caron -Huot & Kasper Larsen 1108. 1180, 1205. 0801, 1208. 1754 & in progress Amplitudes 2013 Schloss Ringberg on the Tegernsee, Germany May 2, 2013

Amplitudes in Gauge Theories • Workshop is testimony to recent years’ remarkable progress at the confluence of string theory, perturbative N=4 SUSY gauge theory, and integrability • One loop amplitudes have led to a revolution in QCD NLO calculations at the multiplicity frontier: first quantitative predictions for LHC, essential to controlling backgrounds • For NNLO & precision physics: need two loops • Sometimes, need two-loop amplitudes just for NLO: gg W +W − LO for subprocess is a one-loop amplitude squared down by two powers of αs, but enhanced by gluon distribution 5% of total cross section @14 Te. V 20– 25% scale dependence 25% of cross section for Higgs search 25– 30% scale dependence Binoth, Ciccolini, Kauer, Krämer (2005) Experiments: measured rate is 10– 15% high? Need NLO to resolve

Two-loop amplitudes Integrand Level Integral Level Mastrolia & Ossola; “Minimal generalized unitarity”: Badger, Frellesvig, & Zhang; just split into trees Mastrolia, Mirabella, Ossola, Peraro; Feng & Huang; Feng, Huang, Luo, Kleiss, Malamos, Papadopoulos, Zheng, & Zhou Verheyen “Maximal generalized unitarity”: Generalization of split as much as possible Ossola–Papadopoulos–Pittau Generalization of at one loop Britto–Cachazo–Feng & Forde This talk On-shell Methods

On-Shell Master Equation • Focus on planar integrals • Terms in c j leading in ε • Work in D=4 for states, integrals remain in D=4− 2ε • Seek formalism which can be used either analytically or purely numerically

Generalized Discontinuity Operators • Cut operations (or ‘projectors’) which satisfy so that applying them to the master equation yields solutions for the c j Important constraint

Putting Lines on Shell • Cutkosky rule

Quadruple Cuts of the One-Loop Box Work in D=4 for the algebra Four degrees of freedom & four delta functions … but are there any solutions?

Do Quadruple Cuts Have Solutions? The delta functions instruct us to solve 1 quadratic, 3 linear equations 2 solutions With k 1, 2, 4 massless, we can write down the solutions explicitly Yes, but…

• Solutions are complex • The delta functions would actually give zero! Need to reinterpret delta functions as contour integrals around a global pole [other contexts: Vergu; Roiban, Spradlin, Volovich; Mason & Skinner] Reinterpret cutting as contour modification

• Global poles: simultaneous on-shell solutions of all propagators & perhaps additional equations • Multivariate complex contour integration: in general, contours are tori • For one-loop box, contours are T 4 encircling global poles

Two Problems • Too many contours (2) for one integral: how should we choose it? • Changing the contour can break equations: is no longer true if we modify the real contour to circle one of the poles Remarkably, these two problems cancel each other out

• Require vanishing Feynman integrals to continue vanishing on cuts • General contour a 1 = a 2

Four-Dimensional Integral Basis •

Planar Double Box • Take a heptacut — freeze seven of eight degrees of freedom • One remaining integration variable z • Six solutions, for example S 2: • Performing the contour integrals enforcing the heptacut Jacobian • Localizes z global pole need contour for z within Si

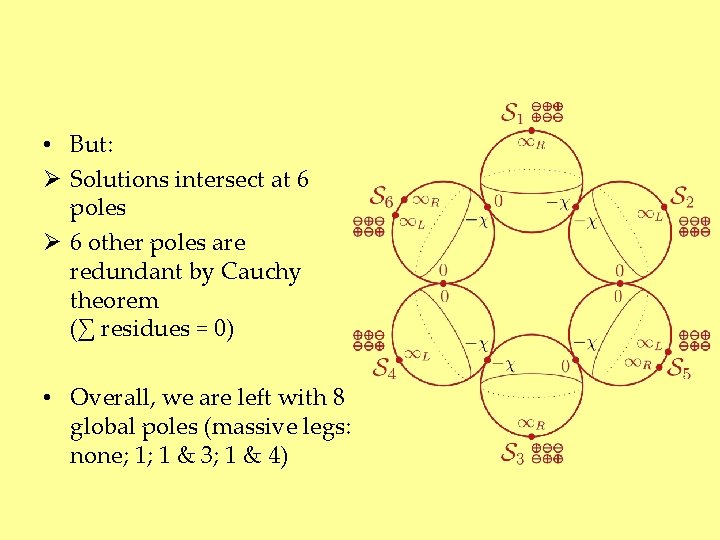
How Many Global Poles Do We Have? Caron-Huot & Larsen (2012) • Parametrization All heptacut solutions have • Here, naively two global poles each at z = 0, −χ 12 candidate poles • In addition, 6 poles at z = from irreducible-numerator ∫s • 2 additional poles at z = −χ− 1 in irreducible-numerator ∫s 20 candidate global poles

• But: Ø Solutions intersect at 6 poles Ø 6 other poles are redundant by Cauchy theorem (∑ residues = 0) • Overall, we are left with 8 global poles (massive legs: none; 1; 1 & 3; 1 & 4)

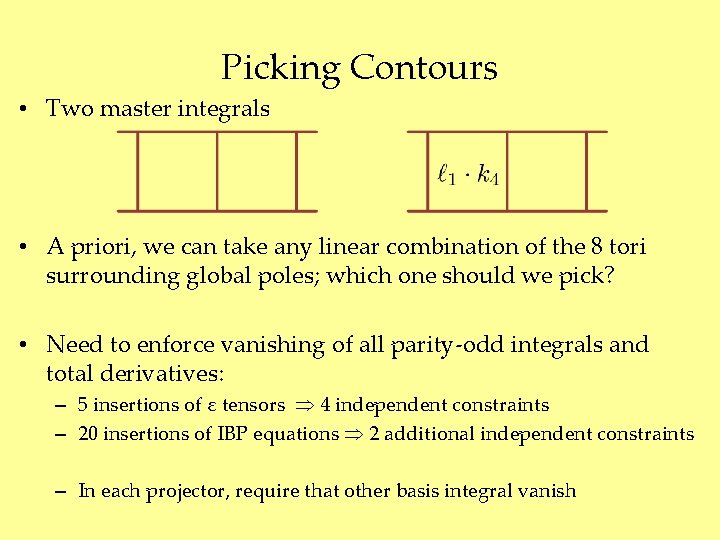
Picking Contours • Two master integrals • A priori, we can take any linear combination of the 8 tori surrounding global poles; which one should we pick? • Need to enforce vanishing of all parity-odd integrals and total derivatives: – 5 insertions of ε tensors 4 independent constraints – 20 insertions of IBP equations 2 additional independent constraints – In each projector, require that other basis integral vanish

• Master formulæ for coefficients of basis integrals to O (ε 0) where P 1, 2 are linear combinations of T 8 s around global poles More explicitly,

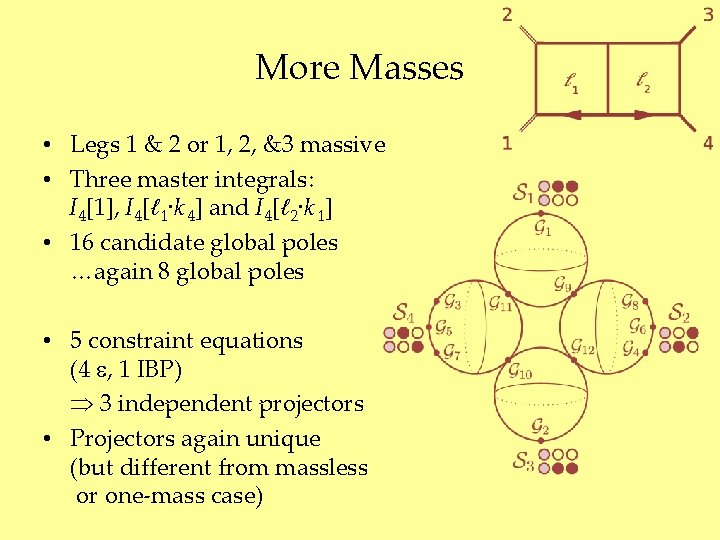
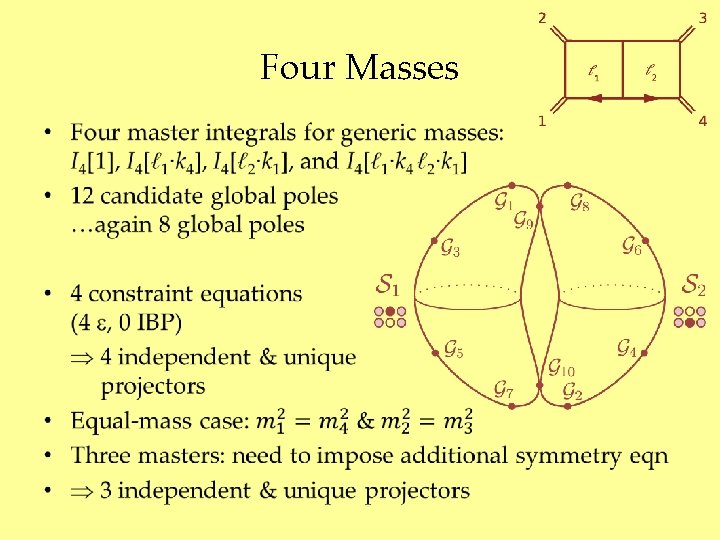
More Masses • Legs 1 & 2 or 1, 2, &3 massive • Three master integrals: I 4[1], I 4[ℓ 1∙k 4] and I 4[ℓ 2∙k 1] • 16 candidate global poles …again 8 global poles • 5 constraint equations (4 , 1 IBP) 3 independent projectors • Projectors again unique (but different from massless or one-mass case)

Four Masses •

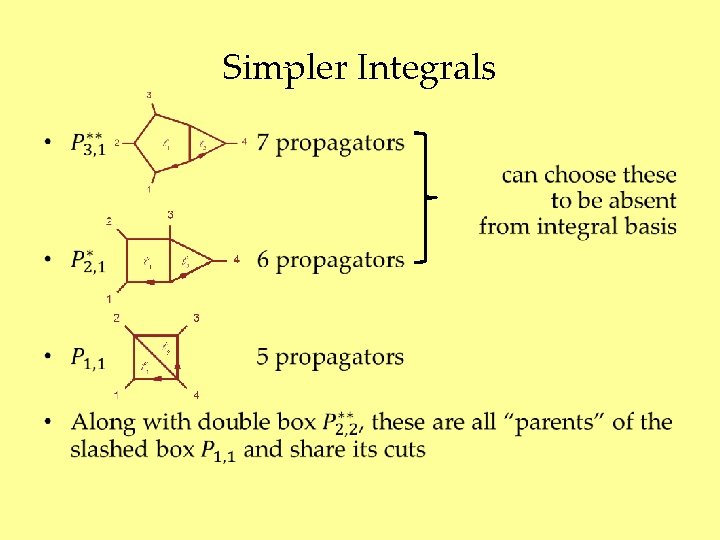
Simpler Integrals •

Slashed Box •

Multivariate Contour Integration •

Summary • First steps towards a numerical unitarity formalism at two loops • Knowledge of an independent integral basis • Criterion for constructing explicit formulæ for coefficients of basis integrals • Four-point examples: double boxes with all external mass configurations; massless slashed box