Les hypothses dtudes de la RDM 1 Les

Les hypothèses d’études de la RDM 1. Les matériaux seront considérés comme homogènes et isotropes, homogène : on dit qu’un matériaux est homogène, s’il possède les mêmes caractéristiques en tous ses points. (Caractéristiques mécaniques) isotrope : on dit qu’un matériaux est isotrope , lorsqu’il possède les mêmes caractéristiques dans toutes les directions.

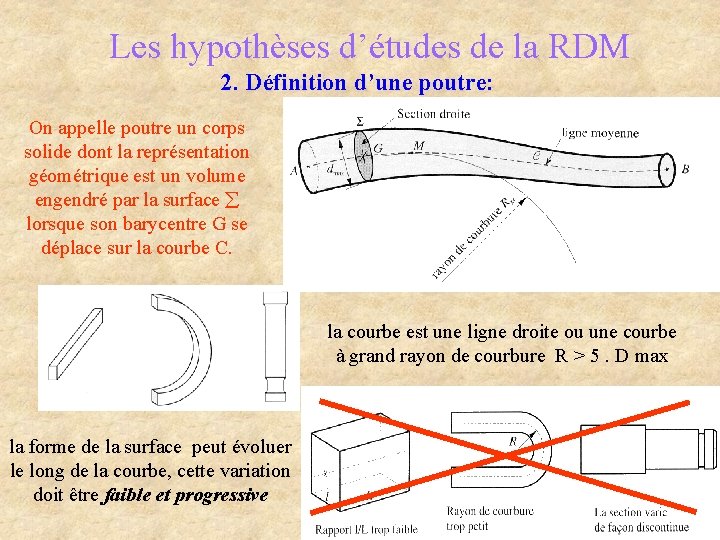
Les hypothèses d’études de la RDM 2. Définition d’une poutre: On appelle poutre un corps solide dont la représentation géométrique est un volume engendré par la surface lorsque son barycentre G se déplace sur la courbe C. la courbe est une ligne droite ou une courbe à grand rayon de courbure R > 5. D max la forme de la surface peut évoluer le long de la courbe, cette variation doit être faible et progressive

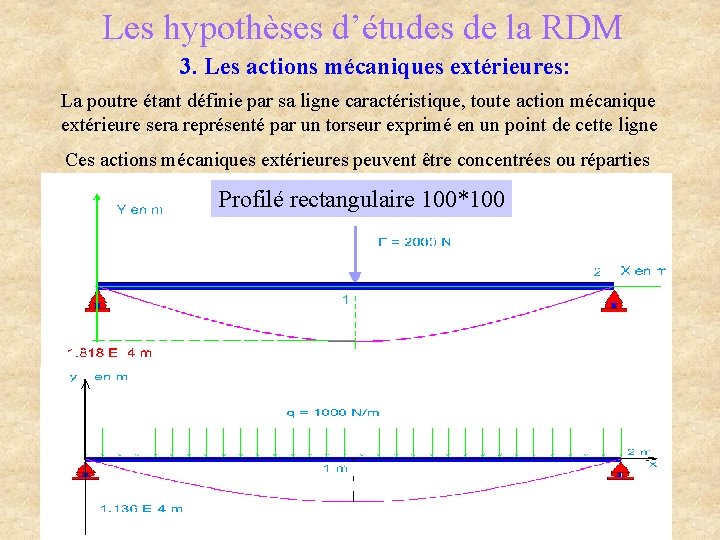
Les hypothèses d’études de la RDM 3. Les actions mécaniques extérieures: La poutre étant définie par sa ligne caractéristique, toute action mécanique extérieure sera représenté par un torseur exprimé en un point de cette ligne Ces actions mécaniques extérieures peuvent être concentrées ou réparties Profilé rectangulaire 100*100

Les hypothèses d’études de la RDM 4. Hypothèses sur les déformations Ordre de grandeur: les déformations ( déplacements des points de la ligne caractéristique) sont petites par rapport aux dimensions de la poutre Hypothèse de Navier-Bernouilli: Toute section droite avant déformation, reste, après déformation, une section droite

Les hypothèses d’études de la RDM 5. Torseur des actions mécaniques de cohésion: N : effort Le torseur des actions mécaniques de cohésion au niveau de la surface représente les actions mécaniques exercées par S+ sur S-. On l’exprime impérativement au point G, barycentre de , et on le projette sur la base locale (x, y, z) Ses composantes se notent conventionnellement Si on étudie l’équilibre de S- on obtient: Si on étudie l’équilibre de S+ on obtient: Normal Mt : moment de torsion Ty : Effort Mfy : moment tranchant suivant y fléchissant suivant y Tz : effort tranchant suivant z Mfz : moment fléchissant suivant z {TAM 1} + {TAM 2} + {TS+ / S-} ={0} {TAM 3} + {TAM 4} + {TS- / S+} ={0} On a donc deux possibilités pour déterminer le torseur des actions mécaniques de cohésion.

Exercice Torseur de cohésion Une poutre 1 est en liaison pivot d’axe (A, z) et en contact ponctuel de normale (D, y) avec un solide 0 Des actions mécaniques extérieures exercées sur 1 sont représentées par deux torseurs en B et C: on donne: A(0, 0, 0) B(1, 0, 0) C(2, 0, 0) D(3, 0, 0) longueur en m 1 A C B D 0 A. Déterminer les inconnues des torseurs des liaisons en A et D B. Écrire le torseur de cohésion le long de la poutre {TS+/S-} C. Tracer les diagrammes N(x), T(x) et Mfz(x)

Exercice Torseur de cohésion A. Déterminer les inconnues des torseurs des liaisons en A et D Si on isole la poutre 1 : elle est soumise à 4 actions mécaniques extérieures Si on applique le P. F. S en A on obtient: On obtient les équations suivantes: 500+XA 0/1=0 -2000+YA 0/1+YD 0/1=0 XA 0/1= -500 N -(1000 1)-(1000 2) +(YD 0/1 3)=0 YA 0/1= 1000 N YD 0/1= 1000 N 1 A C B 0 D

Exercice Torseur de cohésion B. Écrire le torseur de cohésion le long de la poutre {TS+/S-} Si on effectue une coupure entre[AB] : avec G(x, 0, 0) et x [0, 1] Si on étudie l’équilibre de S- on obtient: 1 A G C B N = +500 N Ty = -1000 N Tz = 0 N x 0 D Mt = 0 N. m Mfy = 0 N. m Mfz = 1000. x (N. m) Si on effectue une coupure entre[AC] : avec G(x, 0, 0) et x [1, 2] Si on étudie l’équilibre de S- on obtient: 1 A B G x 0 C N = 0 N Ty = 0 N Tz = 0 N D Mt = 0 N. m Mfy = 0 N. m Mfz = 1000 (N. m)

Exercice Torseur de cohésion Si on effectue une coupure entre[AD] : avec G(x, 0, 0) et x [2, 3] 1 C B A G D N = 0 N Ty = 1000 N Tz = 0 N x 0 Mt = 0 N. m Mfy = 0 N. m Mfz = 1000. (3 -x) (N. m) C. Tracer les diagrammes N(x), T(x) et Mfz(x) Ty en Newton N en Newton 1000 500 1 2 1 3 x en m -1000 Mfz en N. m 1000 1 2 3 x en m

Les hypothèses d’études de la RDM 6. Notion de contrainte Définition du vecteur contrainte : Une coupure est effectuée au niveau de la surface soit M un point de cette surface soit un élément de surface d autour de M, l’effort élémentaire transmissible par entre S+ et S on appelle vecteur contrainte au point M pour la coupure Unités : de normale le vecteur : - en N - en m 2 - - en Pa ou Mpa Contrainte normale et contrainte tangentielle : Si on fait une projection vectorielle du vecteur , on obtient : σ τ Où est le vecteur contrainte normale et est le vecteur contrainte tangentielle.

Les hypothèses d’études de la RDM 6. Notion de contrainte Si on projette ce vecteur dans la base on obtient est la composante normale est la composante tangentielle suivant Relation entre contrainte et torseur de cohésion en G. avec N = Si on généralise ce torseur pour tous les points de la surface , on montre que Mt : Ty = Mfy : Tz = Mfz :

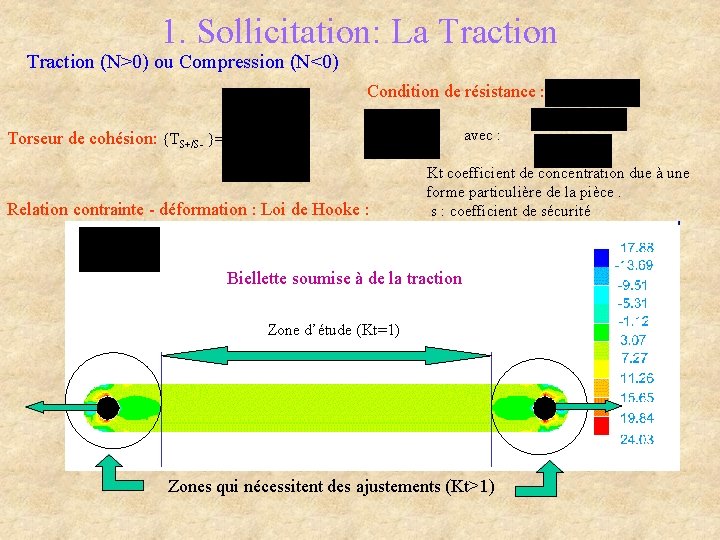
1. Sollicitation: La Traction (N>0) ou Compression (N<0) Condition de résistance : avec : Torseur de cohésion: {TS+/S- }= Relation contrainte - déformation : Loi de Hooke : Kt coefficient de concentration due à une forme particulière de la pièce. s : coefficient de sécurité Biellette soumise à de la traction Zone d’étude (Kt=1) Zones qui nécessitent des ajustements (Kt>1)

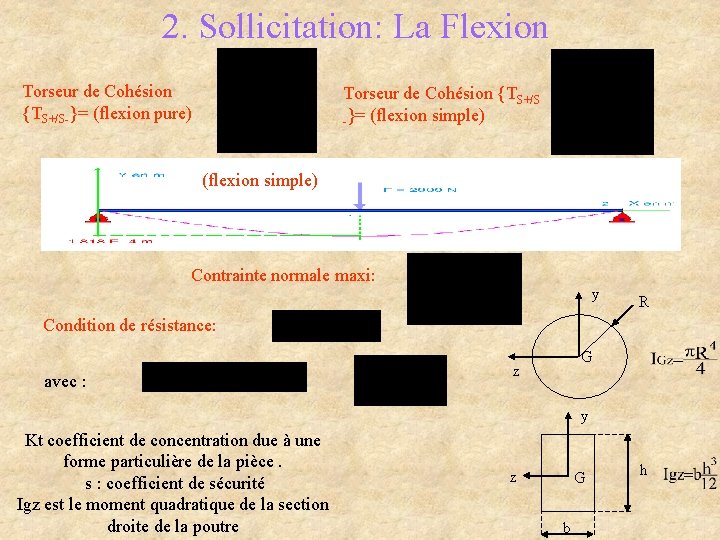
2. Sollicitation: La Flexion Torseur de Cohésion {TS+/S- }= (flexion pure) Torseur de Cohésion {TS+/S -}= (flexion simple) Contrainte normale maxi: y R Condition de résistance: avec : G z y Kt coefficient de concentration due à une forme particulière de la pièce. s : coefficient de sécurité Igz est le moment quadratique de la section droite de la poutre z G b h

Exercice sur la Flexion I Présentation: • La potence ci-dessous permet de soulever des charges de 500 Kg maximum quand le palan 4 se trouve à l’extrémité de la flèche 1. • Cette flèche ainsi que l’équerre 3 forment un ensemble articulé avec le fût 2. • Le fût est fixé au sol. • L’étude porte sur la flèche 1 considérée encastrée avec l’équerre 3. II - DONNÉES : Profilé constituant la flèche 1 : IPE 200 en acier S 355 ; Re = 355 Mpa Hypothèses : Le poids propre de la poutre est négligé. Modélisation: III – TRAVAIL DEMANDÉ : 2. 2 m B A 5000 N 1. Connaissant le torseur de cohésion le long de la poutre, en déduire les types de sollicitation supportées par cette poutre. 2. Déterminer la contrainte maxi, en déduire le coefficient de sécurité adopté pour cette

Exercice sur la Flexion Modélisation: 1. On donne le torseur de cohésion le long de la poutre: A x B G 5000 N Ty en Newton 2. 2 La poutre est soumise à de la flexion simple: - du cisaillement Ty= -5000 N - de la flexion: Mfz= -5000(2. 2 -x) x en m -5000 Mfz en N. m 2. Calcul de la contrainte maxi: 2. 2 x en m -11000