Lenzs Law Induced Current and Electric Fields AP








- Slides: 15

-Lenz’s Law -Induced Current and Electric Fields AP Physics C Mrs. Coyle

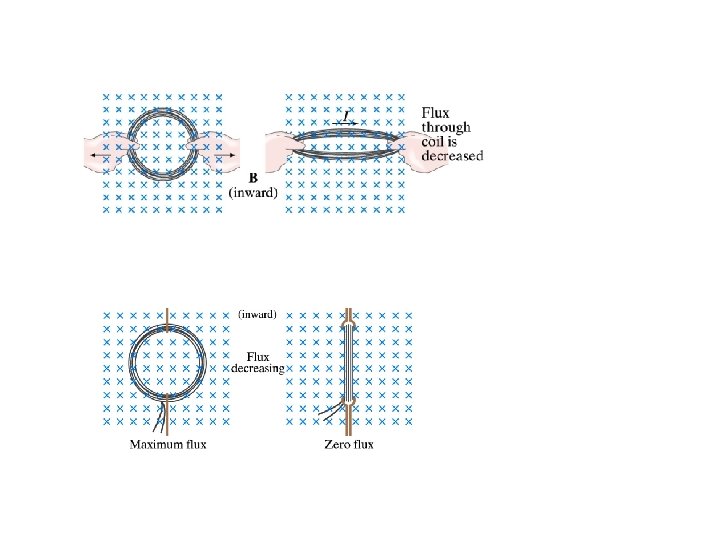
Faraday’s Law of Induction • The emf, E induced in a circuit is directly proportional to the time rate of change of the magnetic flux through the circuit” • Note: The induced emf and the change in flux have opposite algebraic signs

What is the direction of the induced current? • Lenz’s Law: The induced current has a magnetic field that opposes the original change in flux through the area enclosed by the loop. • Indicated by minus (–) sign in Faraday’s equation. • Heinrich Lenz

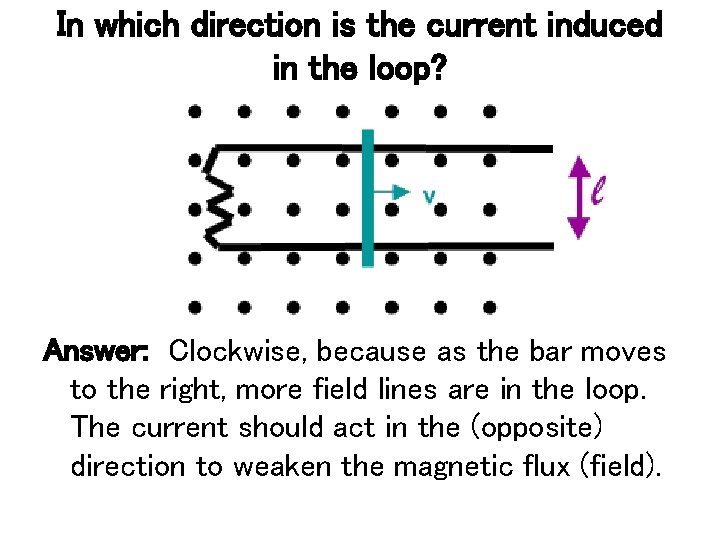
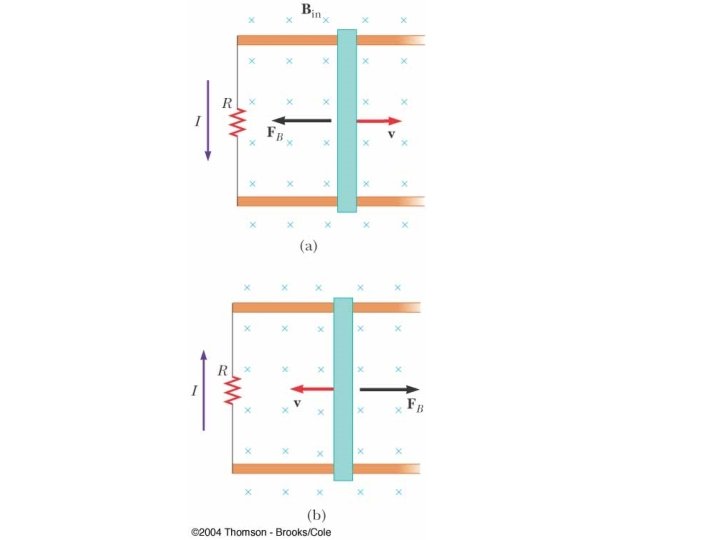
In which direction is the current induced in the loop? Answer: Clockwise, because as the bar moves to the right, more field lines are in the loop. The current should act in the (opposite) direction to weaken the magnetic flux (field).

Example: Change in Area What is the direction of the induced current? Before After • The new smaller area contains less field lines (in the area), so the current will act in direction to strengthen the magnetic field, so the current will be induced clockwise.





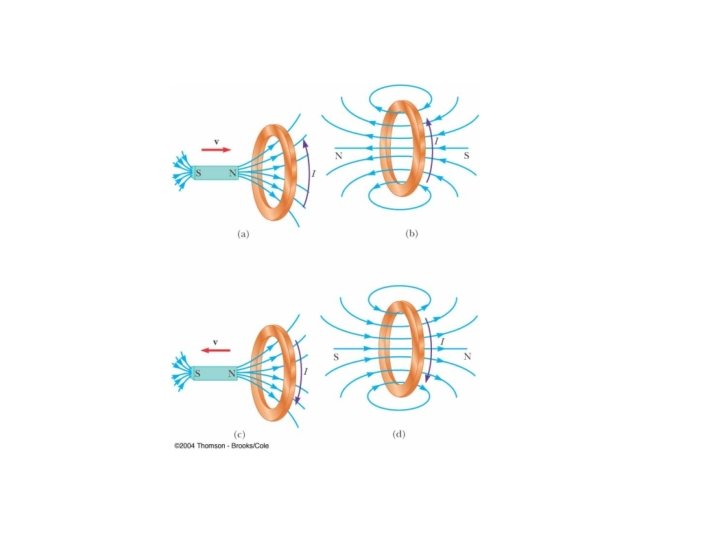
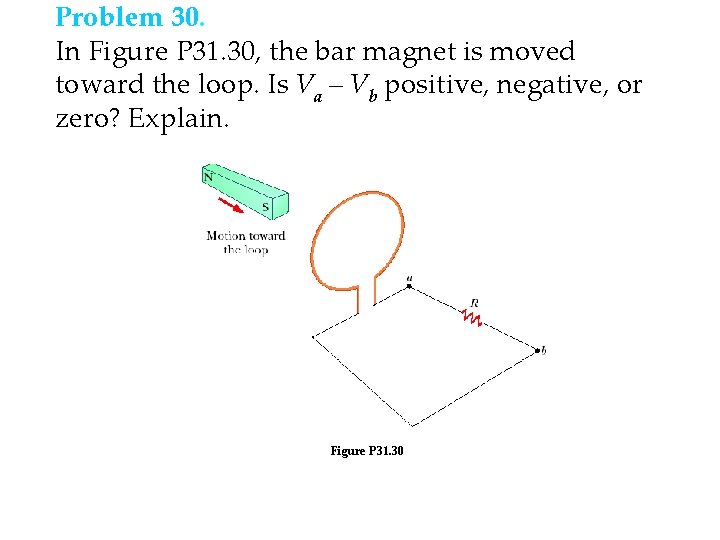
Problem 30. In Figure P 31. 30, the bar magnet is moved toward the loop. Is Va – Vb positive, negative, or zero? Explain. Figure P 31. 30

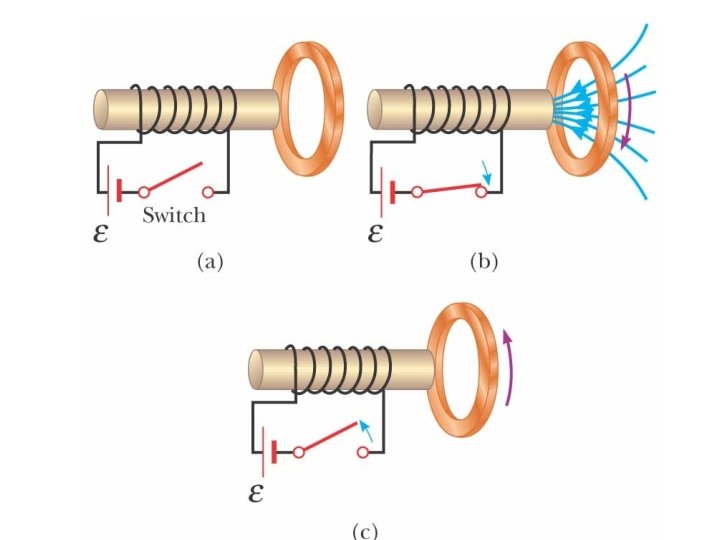
Generator http: //www. walterfendt. de/ph 14 e/generator_e. htm

Induced emf and Electric Fields • An electric field is created in the conductor as a result of the changing magnetic flux • Even in the absence of a conducting loop, a changing magnetic field will generate an electric field in empty space • This induced electric field is nonconservative – Unlike the electric field produced by stationary charges

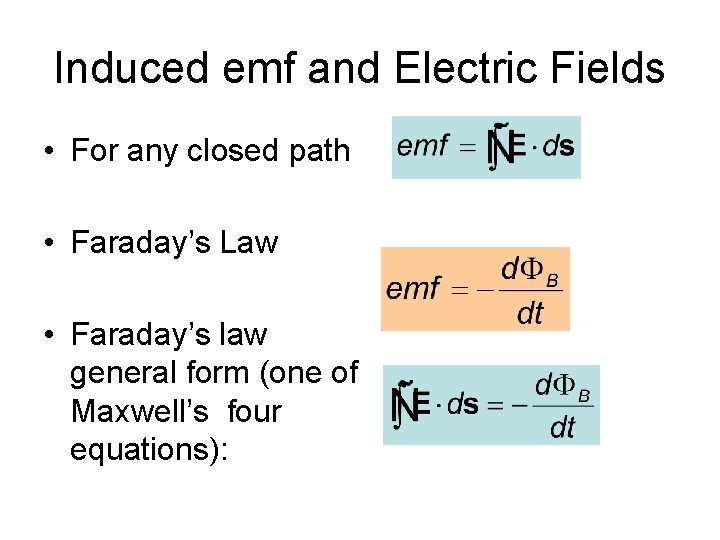
Induced emf and Electric Fields • For any closed path • Faraday’s Law • Faraday’s law general form (one of Maxwell’s four equations):

Note • The induced electric field that is generated by a changing magnetic field is a nonconservative field • The field cannot be an electrostatic field because if the field were electrostatic, and hence conservative, the line integral of E. ds would be zero and it isn’t

Problem 32 For the situation shown, the magnetic field changes with time according to the expression B = (2. 00 t 3 – 4. 00 t 2 + 0. 800)T, and r 2 = 2 R = 5. 00 cm. (a) Calculate the magnitude and direction of the force exerted on an electron located at point P 2 when t = 2. 00 s. (a) At what time is this force equal to zero? Hint: F = q. E + qv x B FE =q. E (Why is FB = 0? )