Latin Square Design Traditionally latin squares have two

Latin Square Design Traditionally, latin squares have two blocks, 1 treatment, all of size n n Yandell introduces latin squares as an incomplete factorial design instead n – Though his example seems to have at least one block (batch) n Latin squares have recently shown up as parsimonious factorial designs for simulation studies

Latin Square Design Motivation n Student project example – 4 drivers, 4 times, 4 routes – Y=elapsed time n Latin Square structure can be natural (observer can only be in 1 place at 1 time) n Observer, place and time are natural blocks for a Latin Square

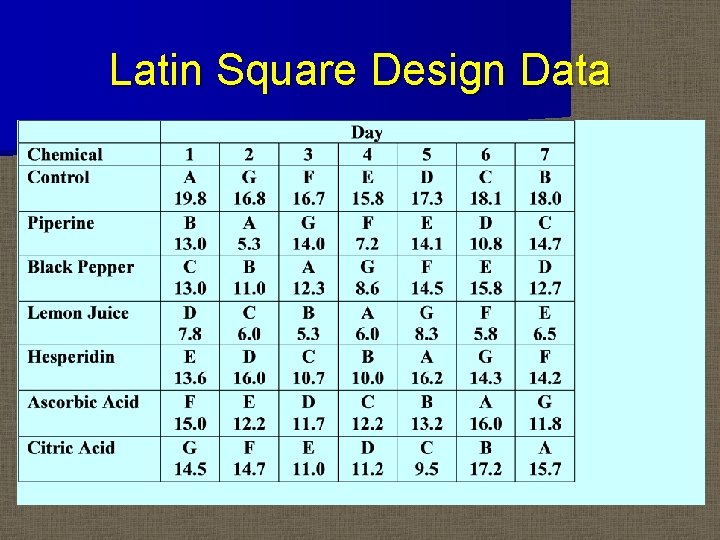
Latin Square Design Example – Region II Science Fair years ago (7 by 7 design) – Row factor—Chemical – Column factor—Day (Block? ) – Treatment—Fly Group (Block? ) – Response—Number of flies (out of 20) not avoiding the chemical

Latin Square Design Data

Power Analysis in Latin Squares n For unreplicated squares, we increase power by increasing n (which may not be practical) n The denominator df is (n-2)(n-1)

Power Analysis in Replicated Latin Squares n For replicated squares, the denominator df depends on the method of replication; see Montgomery

Graeco-Latin Square Design n Suppose we have a Latin Square Design with a third blocking variable (indicated by font color): A B C D A B C

Graeco-Latin Square Design (Fonts) n Suppose we have a Latin Square Design with a third blocking variable (indicated by font style): A B C D A B C

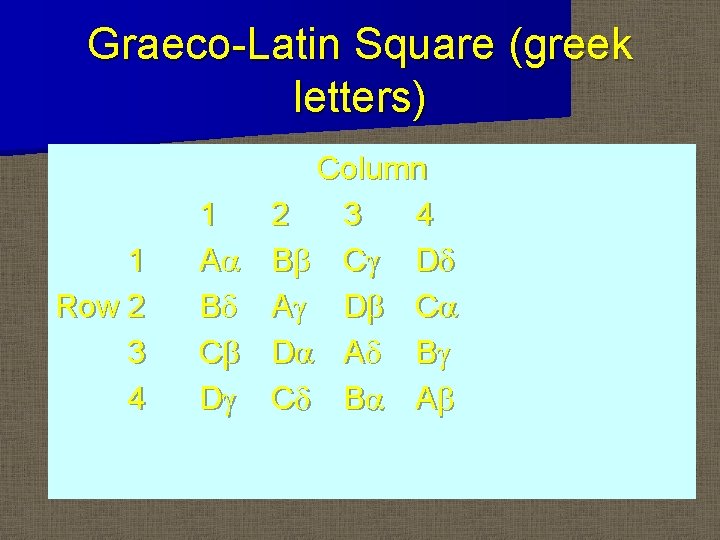
Orthonolaity in Graeco-Latin Squares n Is the third blocking variable orthogonal to the treatment and blocks? n How do we account for the third blocking factor? n We will use Greek letters to denote a third blocking variable

Orthogonal Graeco-Latin Square (colors) A B C D B A D C C D A B D C B A

Orthogonal Graeco-Latin Square (fonts) A B C D B A D C C D A B D C B A

Graeco-Latin Square (greek letters) 1 Row 2 3 4 1 Aa Bd Cb Dg Column 2 3 4 B b Cg Dd A g Db Ca Da A d B g Cd B a A b

Graeco-Latin Square Randomization n Orthogonal designs do not exist for n=6 n Randomization – Standard square – Rows – Columns – Latin letters – Greek letters

Graeco-Latin Square Inference n Total df is n 2 -1=(n-1)(n+1) n Maximum number of blocks is n-1 – n-1 df for Treatment – n-1 df for each of n-1 blocks--(n-1)2 df – n-1 df for error n Hypersquares (# of blocks > 3) are used for screening designs

Conclusions n We will explore some interesting extensions of Latin Squares in the text’s last chapter – Replicated Latin Squares – Crossover Designs – Residual Effects in Crossover designs n But first we need to learn some more about blocking…