JTP A Query Answering System For Knowledge Represented



















- Slides: 23

JTP A Query Answering System For Knowledge Represented in DAML Richard Fikes Gleb Frank 7/12/02 1 Jessica Jenkins Knowledge Systems Laboratory Stanford University www. ksl. stanford. edu Knowledge Systems Laboratory, Stanford University

Hybrid Reasoning for Answering Queries u JTP has a hybrid reasoning architecture 4 First-order logic model elimination theorem prover 4 Suite of special purpose reasoners 4 Dispatchers and APIs for reasoners u Infers query answers that are logical constants 4 Explicitly mentioned in the KB, or 4 Defined in DAML+OIL u Implemented in JAVA u Available from the Web 4 Used by SAIC in ARDA’s AQUAINT program 4 Used by UWF and NAI in DARPA’s Ultra. Log program 4 To be used by BBN in DARPA’s DAML program 2 Knowledge Systems Laboratory, Stanford University

JTP’s DAML+OIL Reasoner u Precomputes most query answers as KB is loaded 4 Enables rapid replies to queries u Based on the axiomatic semantics for DAML+OIL u Compiles axioms into forward chaining actions E. g. , the following axiom: (=> (and (one. Of ? c ? l) (item ? l ? x)) (type ? x ? c)) compiles into an action that > Fires whenever a class C is asserted to be “one. Of” a list L. > Activates an action that – Fires when an object X is asserted to be an “item” of L. – Asserts that X is type C. u Efficiently stores DAML+OIL sentences (triples) E. g. , linking of values of transitive properties such as sub. Class. Of 3 Knowledge Systems Laboratory, Stanford University

Recent Developments u Usability improvements for KB testing and debugging 4 Support for rapid reloading and changing of developing KBs > Load multiple KB modules with checkpointing after each load > “untell” command using “undo”, “redo”, and checkpoints 4 Significant reduction in time required to load KBs u Hierarchical display of reasoning explanations 4 Includes template-based “natural language” descriptions E. g. , “(used. Encryption. Algorithm C-001 A)” displayed as “Algorithm A is used to encrypt communication C-001” Added classifier to DAML+OIL reasoner u Developing reasoners for time-dependent answers u 4 Based on a reusable time ontology developed at KSL E Expanding inferences made by DAML+OIL reasoner 4 Knowledge Systems Laboratory, Stanford University

Negation Using Complements u DAML+OIL does not include explicit negation I. e. , cannot say “(not …)” in DAML+OIL u Negation is related to complements via these axioms: 4 “If NC is the complement of C, then X is not type C exactly when X is type NC. ” (=> (complement. Of ? c ? nc) (<=> (not (type ? x ? c)) (type ? x ? nc))) 4 “If R is the class of all objects that have Y as a value of property P and NR is the complement of R, then Y is not a value of P for X exactly when X is type NR. ” (=> (and (on. Property ? r ? p) (has. Value ? r ? y) (complement. Of ? r ? nr)) (<=> (not (holds ? p ? x ? y)) (type ? x ? nr))) 5 Knowledge Systems Laboratory, Stanford University

Inferring Negations Using Complements u Consider the defining axiom for to. Class restrictions “If R is the class of objects all of whose values of P are type C, X is type R, and V is a value of P for X, then V is type C. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (holds ? p ? x ? v)) (type ? v ? c)) u That axiom is equivalent to the following: “If R is the class of objects all of whose values of P are type C, X is type R, and V is not type C, then V is not a value of P for X. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (not (type ? v ? c))) (not (holds ? p ? x ? v))) 6 Knowledge Systems Laboratory, Stanford University

Inferring Negations Using Complements u The axiom: “If R is the class of objects all of whose values of P are type C, X is type R, and V is not type C, then V is not a value of P for X. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (not (type ? v ? c))) (not (holds ? p ? x ? v))) is equivalent to: “If R is the class of objects all of whose values of P are type C, X is type R, CC is the complement of C, V is type CC, R 2 is the class of objects that have V as a value of P, and CR 2 is the complement of R 2, then X is type CR 2. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (complement. Of ? cc) (type ? v ? cc) (on. Property ? r 2 ? p) (has. Value ? r 2 ? v) (complement. Of ? r 2 ? cr 2)) (type ? x ? cr 2))) which can be used as a forward chaining rule. (!) 7 Knowledge Systems Laboratory, Stanford University

Compiling Actions For Complements u JTP compiles implicative normal form sentences into forward chaining actions (=> (and L 1 … Ln) Lx) is compiled into an action that fires when an Li is asserted u Rule compiler will be expanded as follows: 4 Produce redundant forms of each input (=> (and L 1 … Li-1 Li+1 … Ln (not Lx)) (not Li)) 4 Replace negations by complements (=> (and L 1 … Li-1 Li+1 … Ln … (complement …) (type …) … (complement …)) (type …)) 4 Produce forward chaining actions from the redundant forms > Essentially adds actions that fire when (not Lx) is asserted 8 Knowledge Systems Laboratory, Stanford University

Subclass Hierarchy Inferred By JTP (Union C 1 … Cn) = ~(Intersect ~C 1 … ~Cn) (Union (Subset C 1 … Cn)) Ci (Intersect (Subset C 1 … Cn)) (Intersect C 1 … Cn) = ~(Union ~C 1 … ~Cn) 9 Knowledge Systems Laboratory, Stanford University

Recognizing Individuals JTP uses forward chaining to recognize individuals u Example identifying forward chaining actions: u 4 “If X is type CSUB and CSUB is a subclass of CSUPER, then X is type CSUPER. ” (=> (and (sub. Class. Of ? csub ? csuper) (type ? x ? csub)) (type ? x ? csuper)) 4 “If the range of property P is R and Y is a value of P for some X, then Y is type R. ” (=> (and (range ? p ? r) (holds ? p ? x ? y)) (type ? y ? r)) 4 “If the domain of property P is D and X has a value for P, then X is type D. ” (=> (and (domain ? p ? d) (holds ? p ? x ? y)) (type ? x ? d)) 4 “If X is equivalent to Y and X is type C, then Y is type C. ” (=> (and (equivalent. To ? x ? y) (type ? x ? c)) (type ? y ? c)) 10 Knowledge Systems Laboratory, Stanford University

Forward Chaining Recognition Actions u “If X is an instance of every item on L and C is the intersection of the items on L, then X is an instance of C. ” (=> (and (intersection. Of ? c ? l) (forall ? i (=> (item ? l ? i) (type ? x ? i)))) (type ? x ? c)) u “If class C is one. Of list L and X is an item of L, then X is type C. ” (=> (and (one. Of ? c ? l) (item ? l ? x)) (type ? x ? c)) u “If R is the class of all objects for which all values of property P are type C, X is type R, and V is a value of P for X, then V is type C. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (holds ? p ? x ? v)) (type ? v ? c)) 11 Knowledge Systems Laboratory, Stanford University

Recognizing Individuals In Complements New compiler will produce recognition actions (!) u Examples u 4“If R is the class of objects all of whose values of P are type C, X is type R, and V is a value of P for X, then V is type C. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (holds ? p ? x ? v)) (type ? v ? c)) From that axiom the compiler produces: “If R is the class of objects all of whose values of P are type C, X is type R, CC is the complement of C, V is type CC, R 2 is the class of objects that have V as a value of P, and CR 2 is the complement of R 2, then X is type CR 2. ” (=> (and (on. Property ? r ? p) (to. Class ? r ? c) (type ? x ? r) (complement. Of ? cc) (type ? v ? cc) (on. Property ? r 2 ? p) (has. Value ? r 2 ? v) (complement. Of ? r 2 ? cr 2)) (type ? x ? cr 2))) 12 Knowledge Systems Laboratory, Stanford University

Recognizing Individuals In Complements u Examples of recognition actions the new compiler will produce 4“If Csub is a subclass of Csuper and X is type Csub, then X is type Csuper. ” (=> (and (sub. Class. Of ? csub ? csuper) (type ? x ? csub)) (type ? x ? csuper)) From that axiom the compiler produces: “If Csub is a subclass of Csuper, C-Csub is the complement of Csub, CCsuper is the complement of Csuper, and X is type C-Csuper, then X is type C-Csub. ” (=> (and (sub. Class. Of ? csub ? csuper) (complement. Of ? ccsub ? csub) (complement. Of ? ccsuper ? csuper) (type ? x ? ccsuper)) (type ? x ? ccsub))) 13 Knowledge Systems Laboratory, Stanford University

Cryptographic Policy Example • In this DAML ontology, Communication. Action. Between. AG 1 And. AG 2 is the class of all actions in which the action is performed. By AG 1 and has. Destination AG 2. http: //ksl. stanford. edu/DAML/ultralog/Cryptographic. Policies 1. daml • There is a restriction on the class that all communications between these two groups must be encrypted with encryption scheme A. 12/15/2021 14

A Specific Communication Instance • Communication-001 is an instance of a communication between group AG 1 and group AG 2. • Note: • Communication-001 is not asserted to be an instance of Communication. Action. Between. AG 1 And. AG 2 • Communication-001 is not asserted to be encrypted. 12/15/2021 15

Here, we ask JTP what algorithm Communication-001 was encrypted with: And the answer is…. 12/15/2021 A (!) 16

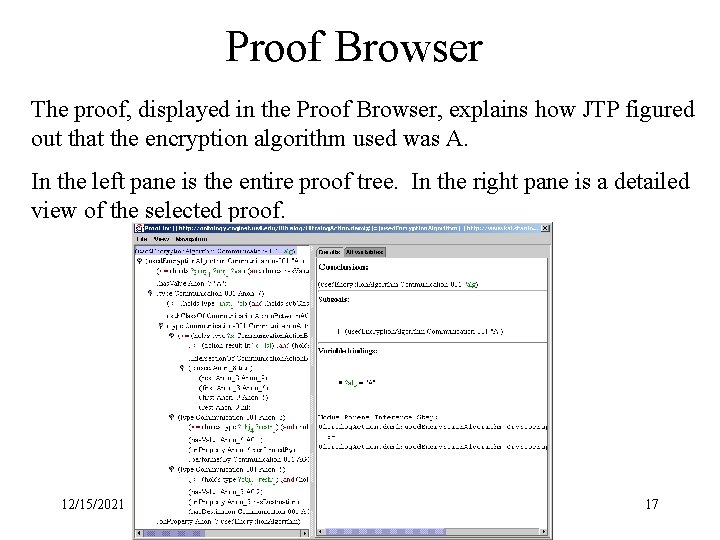
Proof Browser The proof, displayed in the Proof Browser, explains how JTP figured out that the encryption algorithm used was A. In the left pane is the entire proof tree. In the right pane is a detailed view of the selected proof. 12/15/2021 17

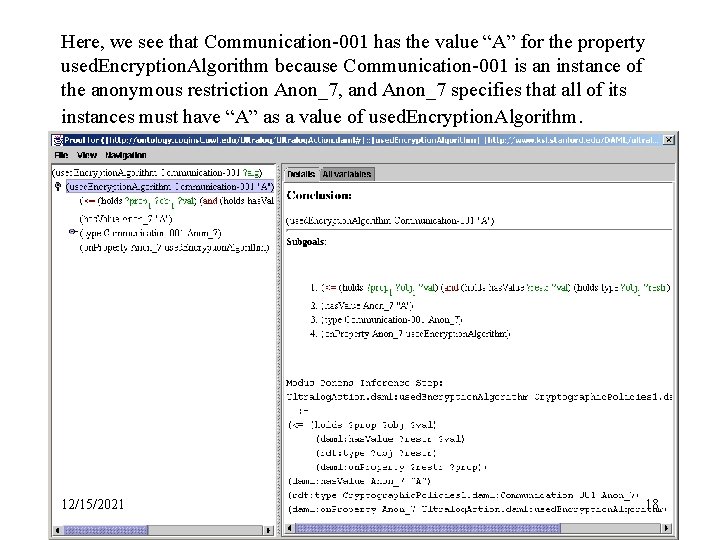
Here, we see that Communication-001 has the value “A” for the property used. Encryption. Algorithm because Communication-001 is an instance of the anonymous restriction Anon_7, and Anon_7 specifies that all of its instances must have “A” as a value of used. Encryption. Algorithm. 12/15/2021 18

Communication-001 is an instance of Anon_7 because it is an instance of Communication. Action. Between. AG 1 And. AG 2, and Communication. Action. Between. AG 1 And. AG 2 is a subclass of Anon_7. But why is Communication-001 an instance of Communication. Action. Between. AG 1 And. AG 2? 12/15/2021 19

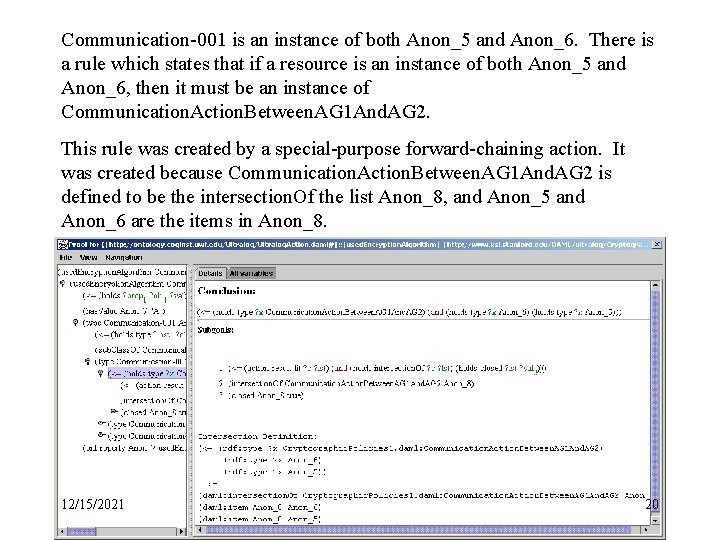
Communication-001 is an instance of both Anon_5 and Anon_6. There is a rule which states that if a resource is an instance of both Anon_5 and Anon_6, then it must be an instance of Communication. Action. Between. AG 1 And. AG 2. This rule was created by a special-purpose forward-chaining action. It was created because Communication. Action. Between. AG 1 And. AG 2 is defined to be the intersection. Of the list Anon_8, and Anon_5 and Anon_6 are the items in Anon_8. 12/15/2021 20

Communication-001 is an instance of the restriction Anon_6 because it has a value AG 1 for the property performed. By. 12/15/2021 21

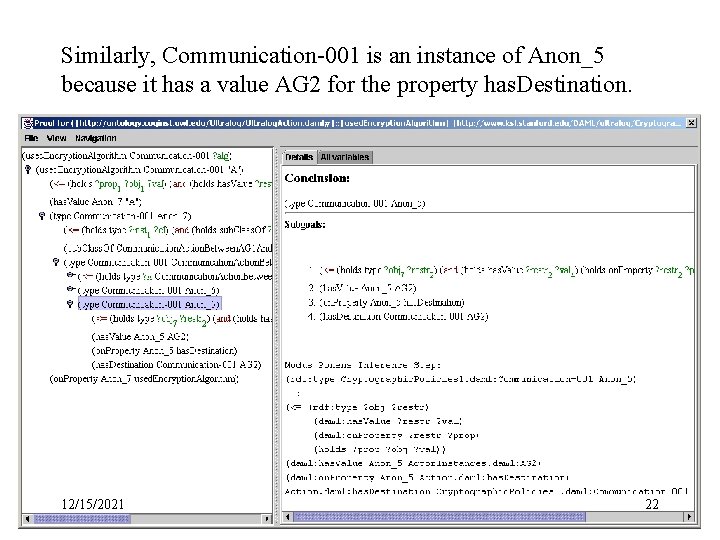
Similarly, Communication-001 is an instance of Anon_5 because it has a value AG 2 for the property has. Destination. 12/15/2021 22

JTP Summary u Hybrid reasoning system for query answering u Special purpose reasoner for DAML+OIL u Easily extendable by adding special purpose reasoners u Current and recent developments 4 Usability improvements for KB testing and debugging 4 Hierarchical display of reasoning explanations > Includes template-based “natural language” descriptions 4 Added classifier to DAML+OIL reasoner 4 Developing reasoners for time-dependent answers > Based on a reusable time ontology developed at KSL 4 Expanding inferences made by DAML+OIL reasoner > Reasoning with complements > Recognizing individuals 23 Knowledge Systems Laboratory, Stanford University