Answering distance queries in directed graphs using fast

Answering distance queries in directed graphs using fast matrix multiplication Raphael Yuster University of Haifa Uri Zwick Tel Aviv University 1

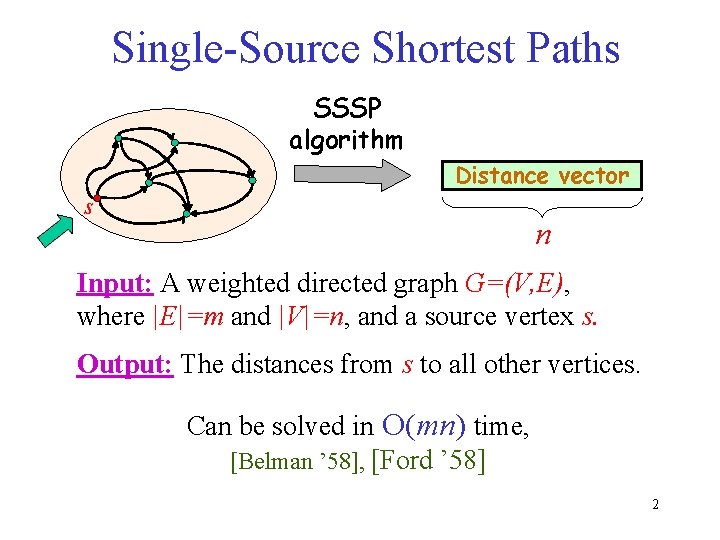
Single-Source Shortest Paths SSSP algorithm Distance vector s n Input: A weighted directed graph G=(V, E), where |E|=m and |V|=n, and a source vertex s. Output: The distances from s to all other vertices. Can be solved in O(mn) time, [Belman ’ 58], [Ford ’ 58] 2

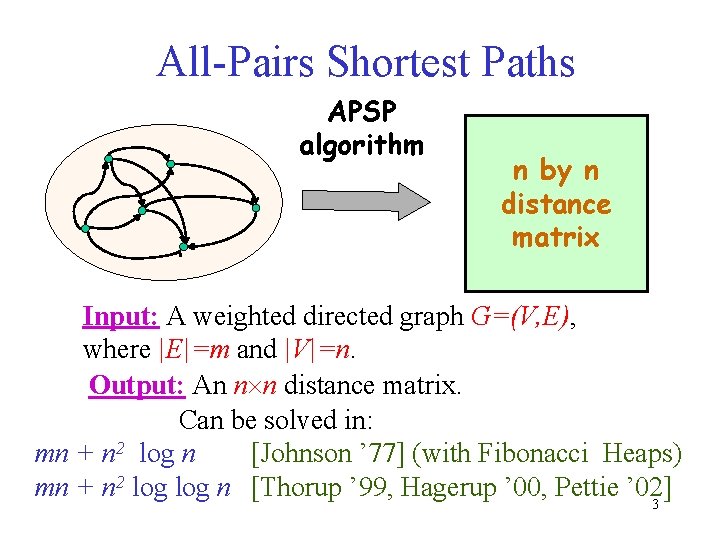
All-Pairs Shortest Paths APSP algorithm n by n distance matrix Input: A weighted directed graph G=(V, E), where |E|=m and |V|=n. Output: An n n distance matrix. Can be solved in: mn + n 2 log n [Johnson ’ 77] (with Fibonacci Heaps) mn + n 2 log n [Thorup ’ 99, Hagerup ’ 00, Pettie ’ 02] 3

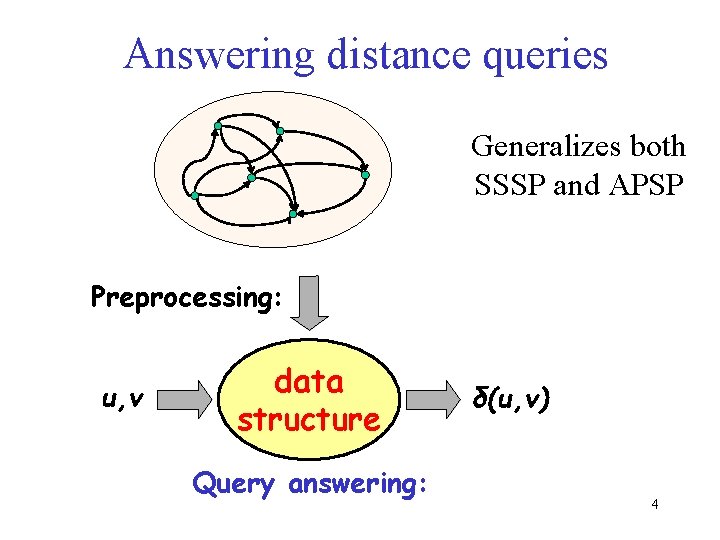
Answering distance queries Generalizes both SSSP and APSP Preprocessing: u, v data structure Query answering: δ(u, v) 4

Single-source Shortest Paths in directed graphs with bounded integer edge weights Running time Authors mn 1/2 log(n) mn 1/2 [Gabow-Tarjan ’ 89] [Goldberg ’ 95] For dense graphs, the running time is O(n 2. 5) ! 5

Assuming bounded integer edge weights: 2. 5 -ε O(n ) Can we get an algorithm for the SSSP problem? Can we get an O(n 3 -ε) algorithm for the APSP problem? Yes! If we are using fast matrix multiplication 6

All-Pairs Shortest Paths in directed graphs with bounded integer weights Running time Authors n 2. 58 [Zwick ’ 98] Improves results of [Alon-Galil-Margalit ’ 91] [Takaoka ’ 98] 7

New result: Answering distance queries Directed graphs, bounded integer weights. Preprocessing time Query time Authors n 2. 38 n [Yuster-Zwick ’ 05] In particular, any n 1. 38 distances can be computed in n 2. 38 time. For dense enough graphs this improves on Goldberg’s SSSP algorithm. n 2. 38 vs. mn 0. 5 8

Min-Plus Products 10

Solving the APSP problem by repeated squaring If W is an n by n matrix containing the edge weights of a graph. Then Wn is the distance matrix. D W for i 1 to log 2 n do D D*D Thus: APSP(n) MPP(n) log n 11

Algebraic Product O(n 2. 38) [Strassen ’ 69] … [Coppersmith. Winograd ’ 90] Min-Plus Product The fast algebraic algorithms cannot be used, as the min operation has no inverse 12

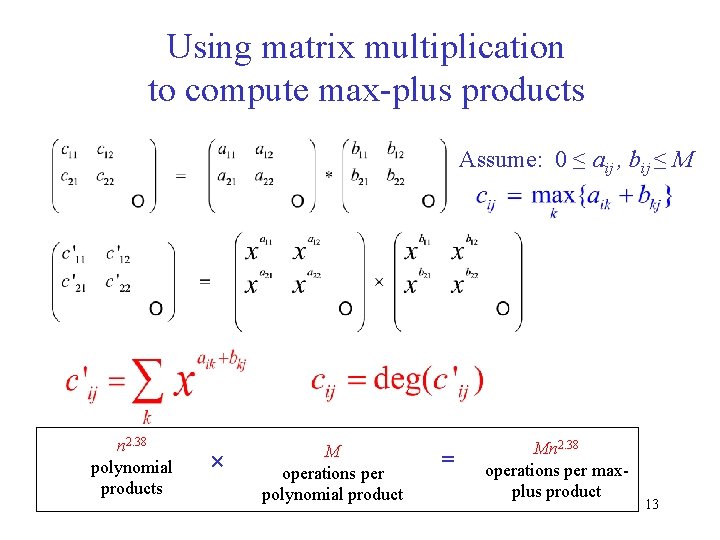
Using matrix multiplication to compute max-plus products Assume: 0 ≤ aij , bij ≤ M n 2. 38 polynomial products M operations per polynomial product = Mn 2. 38 operations per maxplus product 13

Trying to implement the repeated squaring algorithm Consider an easy case: all weights are 1. * Iteration Max size of elements Cost 1 2 i log n 1 2 2 i n n 2. 38 2·n 2. 38 2 i·n 2. 38 n·n 2. 38 14

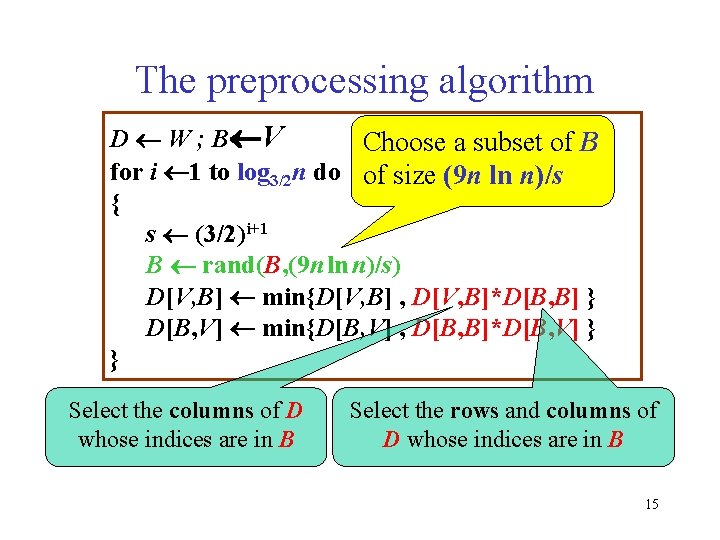
The preprocessing algorithm D W ; B V Choose a subset of B for i 1 to log 3/2 n do of size (9 n ln n)/s { s (3/2)i+1 B rand(B, (9 n ln n)/s) D[V, B] min{D[V, B] , D[V, B]*D[B, B] } D[B, V] min{D[B, V] , D[B, B]*D[B, V] } } Select the columns of D whose indices are in B Select the rows and columns of D whose indices are in B 15

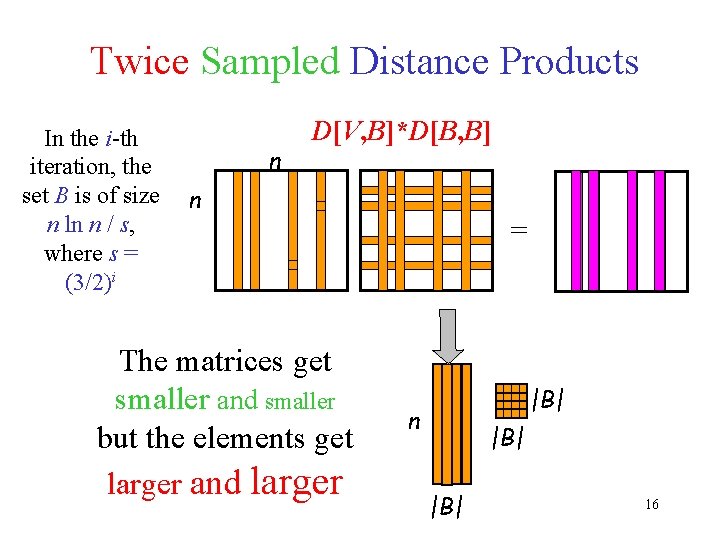
Twice Sampled Distance Products In the i-th iteration, the set B is of size n ln n / s, where s = (3/2)i n D[V, B]*D[B, B] n The matrices get smaller and smaller but the elements get larger and larger = |B| n |B| 16

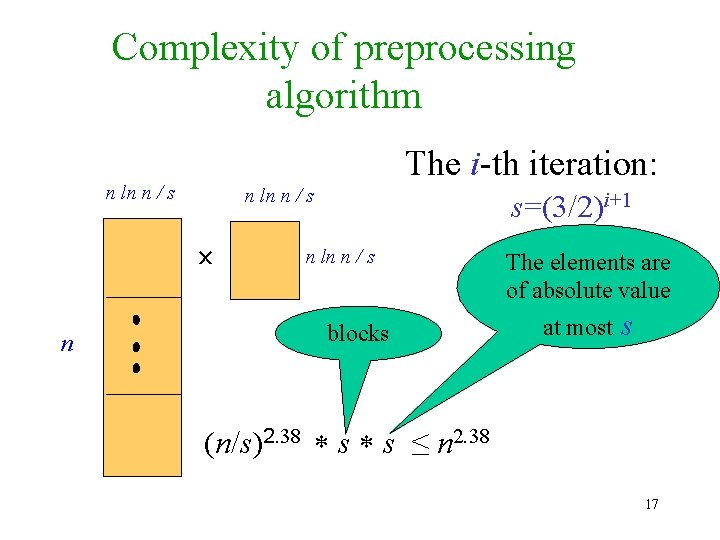
Complexity of preprocessing algorithm The i-th iteration: n ln n / s n s=(3/2)i+1 n ln n / s blocks The elements are of absolute value at most s (n/s)2. 38 s s ≤ n 2. 38 17

The query answering algorithm δ(u, v) D[{u}, V]*D[V, {v}] v u Query time: O(n) 18

The preprocessing algorithm: Correctness Let Bi be the i-th sample. B 1 B 2 B 3 … Invariant: After the i-th iteration, if (u V and v Bi) or (v V and u Bi) and there is a shortest path from u to v that uses at most (3/2)i edges, then D(u, v)=δ(u, v). Consider a shortest path that uses at most (3/2)i+1 edges at most 19

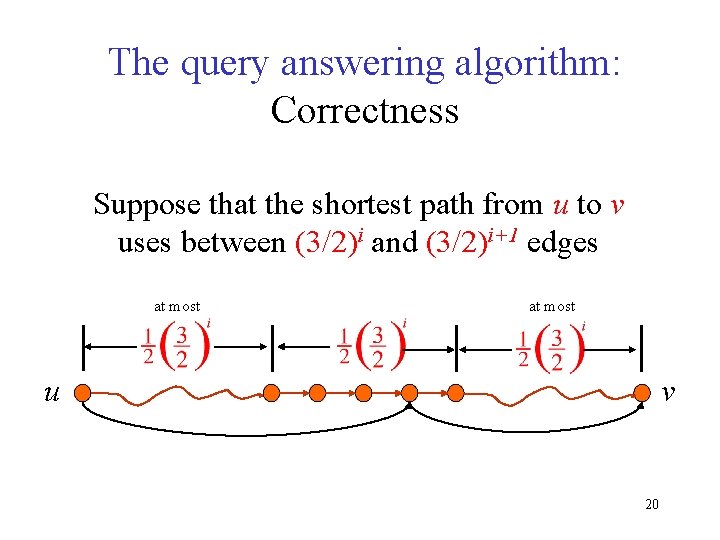
The query answering algorithm: Correctness Suppose that the shortest path from u to v uses between (3/2)i and (3/2)i+1 edges at most u v 20