Graph property Every Monotone Graph Property has a

Graph property Every Monotone Graph Property has a sharp threshold

Graph property n n A graph property is a property of graphs which is closed under isomorphism. monotone graph property : Let P be a graph property. n Every graph H on the same set of vertices, which contains G as a sub graph satisfies P as well. n

Examples of graph properties G is connected n G is Hamiltonian n G contains a clique of size t n G is not planar n The clique number of G is larger than that of its complement n the diameter of G is at most s n. . . etc. n

Erdös – Rényi Graph n n Model Erdös - Rényi for random graph Choose every edge with probability p

Erdös – Rényi Graph n n Model Erdös - Rényi for random graph Choose every edge with probability p

Every Monotone Graph Property has a sharp threshold Ehud Friedgut & Gil Kalai

Definitions n GNP – a graph property n (P) - the probability that a random n graph on n vertices with edge probability p satisfies GP. G G(n, p) - G is a random graph with n vertices and edge probability p.

Main Theorem n Let GNP be any monotone property of graphs on n vertices. If p(GNP) > then q(GNP) > 1 - for q = p + c 1 log(1/2 )/logn absolute constant

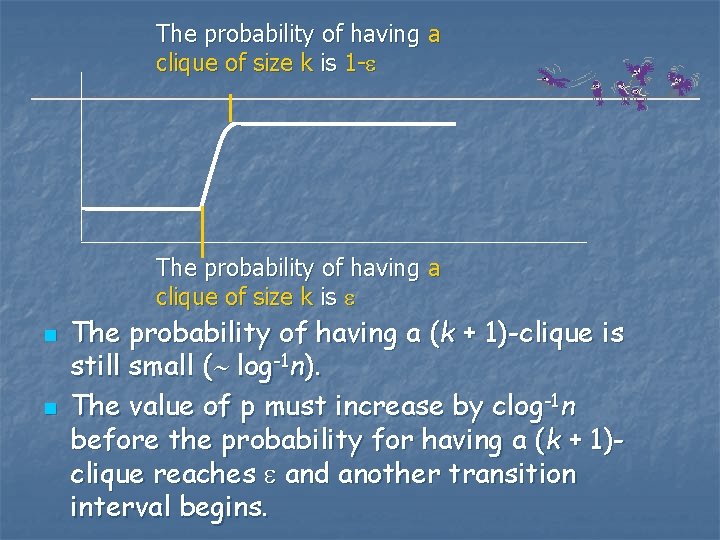
Example-Max Clique n n n Probability for choosing an edge Consider G G(n, p). Number of The length of the interval of vertices probabilities p for which the clique number of G is almost surely k (where k log n) is of order log-1 n. The threshold interval: The transition between clique numbers k-1 and k.

The probability of having a clique of size k is 1 - The probability of having a clique of size k is n n The probability of having a (k + 1)-clique is still small ( log-1 n). The value of p must increase by clog-1 n before the probability for having a (k + 1)clique reaches and another transition interval begins.

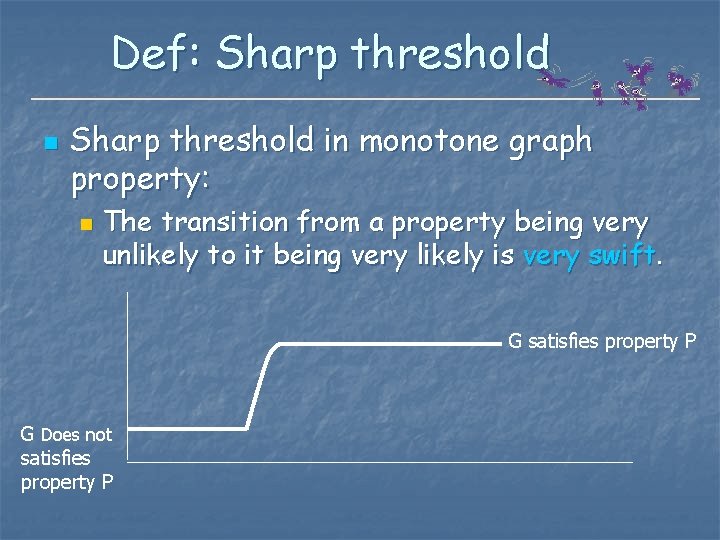
Def: Sharp threshold n Sharp threshold in monotone graph property: n The transition from a property being very unlikely to it being very likely is very swift. G satisfies property P G Does not satisfies property P

Conjecture n Let GNP be any monotone property of graphs on n vertices. If p(GNP) > then q(GNP) > 1 - for q = p + clog(1/2 )/log 2 n