Triangulation of Monotone Polygon Triangulating a monotone polygon






- Slides: 13

Triangulation of Monotone Polygon Triangulating a monotone polygon, introduction The algorithm to triangulate a monotone polygon depends on its monotonicity. Developed in 1978 by Garey, Johnson, Preparata, and Tarjan, it is described in both Preparata pp. 239 -241 (1985) and Laszlo pp. 128 -135 (1996). The former uses y-monotone polygons, the latter uses x-monotone. Initialization Sort the N vertices of monotone polygon P in order by decreasing y coordinate. (Here N is the number of vertices of P, not S. ) The sort can be done in O(N) time, not O(N log N), by merging the two monotone chains of P. Let u 1, u 2, …, u. N be the sorted sequence of vertices, so y(u 1) > y(u 2) > … > y(u. N). Because of the regularization process and the monotonicity of P, for every ui 1 i < N there exists uj 1 < j N such that edge uiuj is an edge of P.

Proximity Constrained triangulation Description of the processing The algorithm processes one vertex at a time in order of decreasing y coordinate, creating diagonals of polygon P. Each diagonal bounds a triangle, and leaves a polygon with one less side still to be triangulated. Stack The algorithm uses a stack to store vertices that have been visited but not yet connected with a diagonal. The stack content is v 1, v 2, …, vi, where v 1 is the bottom and vi the top of the stack. At any time during the execution, there are two invariants: 1. The vertices v 1, v 2, …, vi on the stack from a chain on the boundary of P, where y(v 1) > y(v 2) > … > y(vi). 2. If i 3, angle vjvj+1 vj+2 for 1 j i - 2.

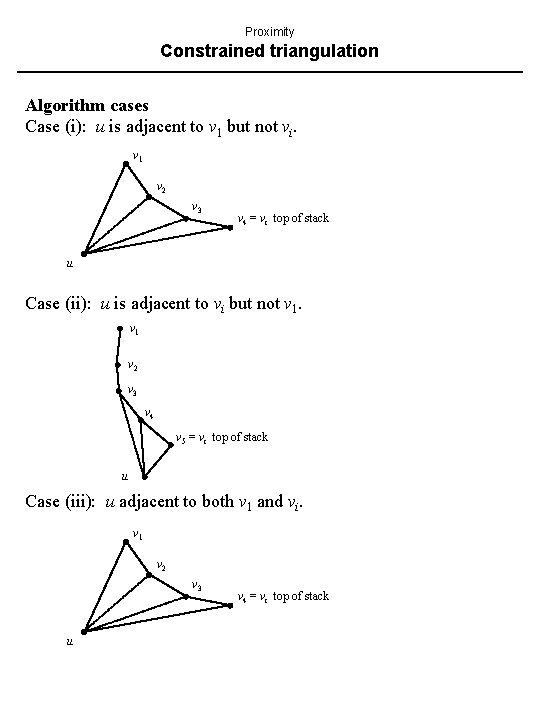
Proximity Constrained triangulation Algorithm By “adjacent” we mean connected by an edge in P. Recall that v 1 is the bottom of the stack, vi is the top. 1. 2. 3. 4. Push u 1 and u 2 on the stack. j = 3 /* j is index of current vertex */ u = uj Case (i): u is adjacent to v 1 but not vi. add diagonals uv 2, uv 3, …, uvi. pop vi, vi-1, …, v 1 from stack. push vi, u on stack. Case (ii): u is adjacent to vi but not v 1. while i > 1 and angle uvivi-1 < add diagonal uvi-1 pop vi from stack endwhile push u Case (iii): u adjacent to both v 1 and vi. add diagonals uv 2, uv 3, …, uvi-1. exit 5. j = j + 1 Go to step 3.

Proximity Constrained triangulation Algorithm cases Case (i): u is adjacent to v 1 but not vi. v 1 v 2 v 3 v 4 = vi top of stack u Case (ii): u is adjacent to vi but not v 1 v 2 v 3 v 4 v 5 = vi top of stack u Case (iii): u adjacent to both v 1 and vi. v 1 v 2 v 3 u v 4 = vi top of stack

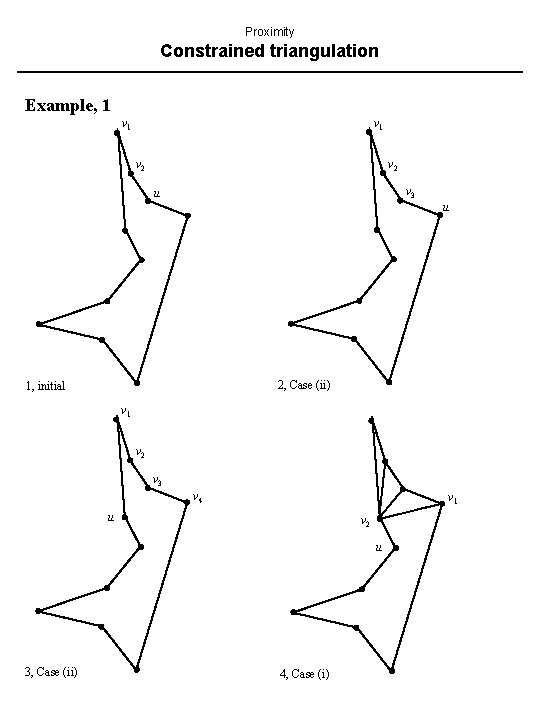
Proximity Constrained triangulation Example, 1 v 1 v 2 v 3 u u 2, Case (ii) 1, initial v 1 v 2 v 3 v 4 v 1 u v 2 u 3, Case (ii) 4, Case (i)

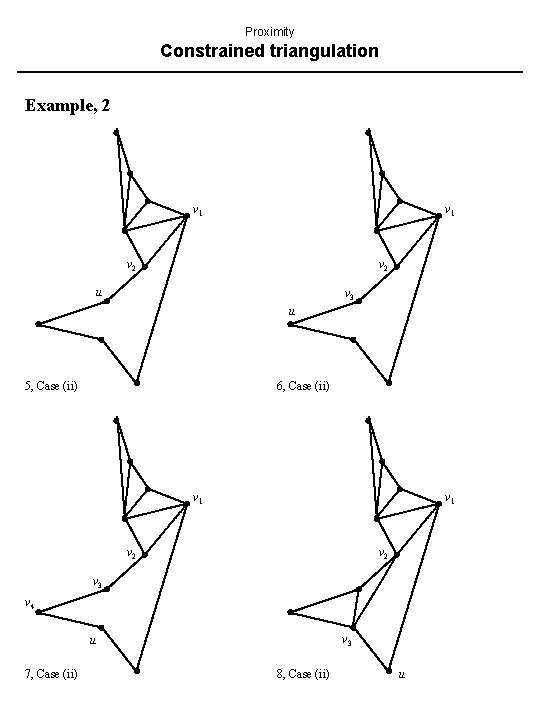
Proximity Constrained triangulation Example, 2 v 1 v 2 u v 3 u 5, Case (ii) 6, Case (ii) v 1 v 2 v 3 v 4 v 3 u 7, Case (ii) 8, Case (ii) u

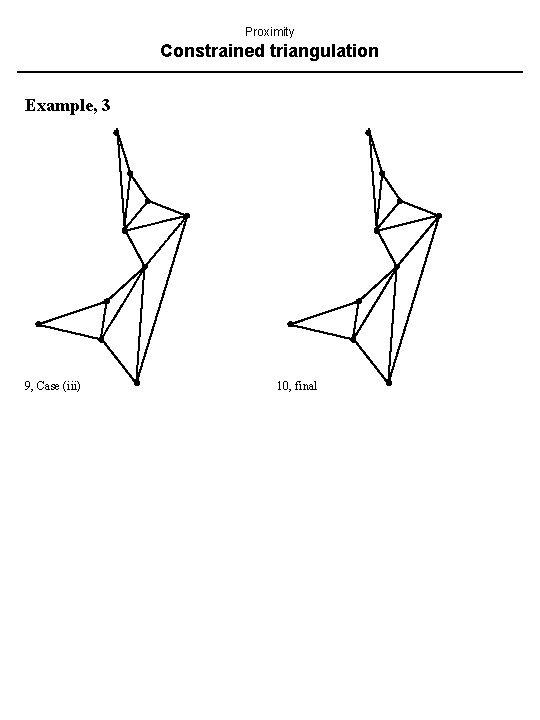
Proximity Constrained triangulation Example, 3 9, Case (iii) 10, final

Proximity Constrained triangulation Proof of correctness The correctness of the algorithm depends on the fact that all the added diagonals lie inside the polygon P. For details, see Preparata pp. 240 -241, or Laszlo pp. 134 -135. Analysis of triangulating a monotone polygon The initial sort (merge) requires O(N) time. Each of the N vertices is visited and placed on the stack exactly once, except when the while fails in case (ii). This happens at most once per vertex, so that time can be charged to the current vertex. The algorithm requires O(N) time to triangulate a monotone polygon, where N is the number of vertices of the polygon.

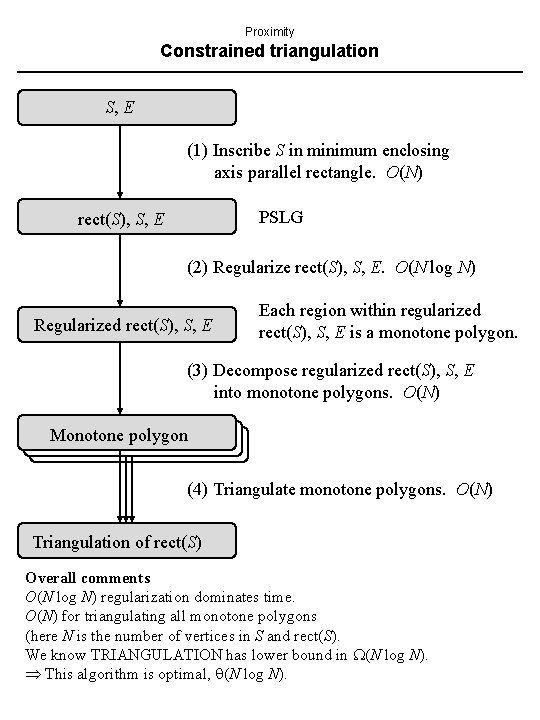
Proximity Constrained triangulation S, E (1) Inscribe S in minimum enclosing axis parallel rectangle. O(N) PSLG rect(S), S, E (2) Regularize rect(S), S, E. O(N log N) Regularized rect(S), S, E Each region within regularized rect(S), S, E is a monotone polygon. (3) Decompose regularized rect(S), S, E into monotone polygons. O(N) Monotone polygon (4) Triangulate monotone polygons. O(N) Triangulation of rect(S) Overall comments O(N log N) regularization dominates time. O(N) for triangulating all monotone polygons (here N is the number of vertices in S and rect(S). We know TRIANGULATION has lower bound in (N log N). This algorithm is optimal, (N log N).

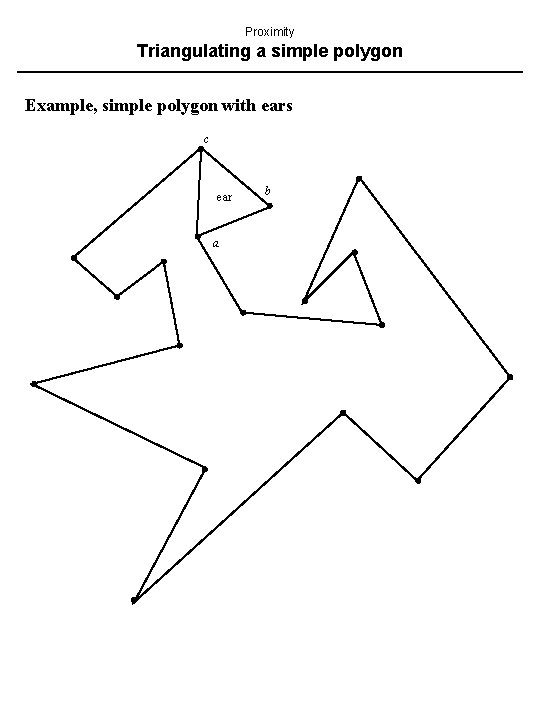
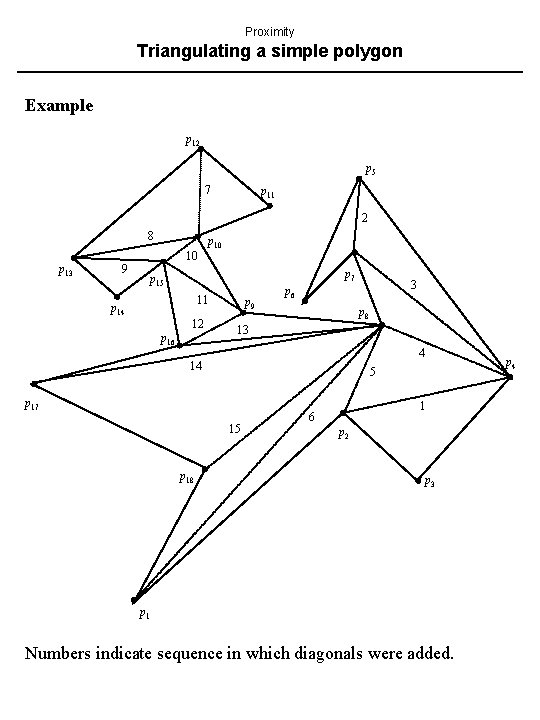
Proximity Triangulating a simple polygon Definitions In a simple polygon, edges intersect only at vertices, and non-adjacent edges do not intersect. Three consecutive vertices a, b, c of a polygon form an ear of the polygon if segment ac is a diagonal; b is the ear tip. Meister’s Two Ears Theorem. Every polygon with N 4 vertices has at least two nonoverlapping ears.

Proximity Triangulating a simple polygon Example, simple polygon with ears c ear a b

Proximity Triangulating a simple polygon Triangulation by otectomy See O’Rourke, pp. 39 -46. Let P be a simple polygon, with vertices {p 1, p 2, …, p. N}. 1. if N > 3 2. for each potential ear diagonal pipi+2 3. if pipi+2 is a diagonal 4. add diagonal pipi+2 5. recurse on P - {pi+1} 6. endif 7. endfor 8. endif Analysis Step 2 is O(N), search around P. Step 3 is a test for diagonal by checking for intersections, O(N). Step 5 can occur at most O(N) times. Overall time required is O(N 3).

Proximity Triangulating a simple polygon Example p 12 p 5 7 p 11 2 8 p 13 p 10 10 9 p 7 p 15 11 p 14 12 p 16 p 9 p 8 13 4 14 p 4 5 p 17 15 p 18 3 p 6 1 6 p 2 p 3 p 1 Numbers indicate sequence in which diagonals were added.