Geometrie pro potaovou grafiku Pklad 3 Geometrie pro

Geometrie pro počítačovou grafiku (Příklad 3)

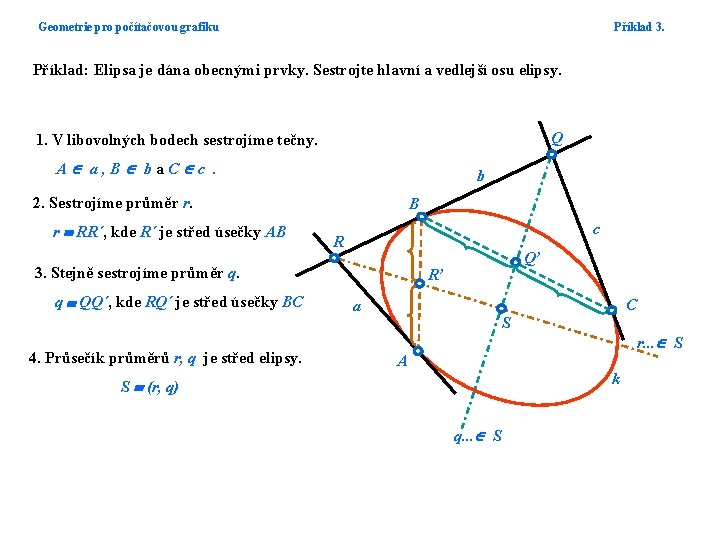
Geometrie pro počítačovou grafiku Příklad 3. Příklad: Elipsa je dána obecnými prvky. Sestrojte hlavní a vedlejší osu elipsy. Q 1. V libovolných bodech sestrojíme tečny. A a, B ba. C c. b 2. Sestrojíme průměr r. r RR´, kde R´ je střed úsečky AB B c R 3. Stejně sestrojíme průměr q. q QQ´, kde RQ´ je střed úsečky BC Q’ R’ C a S 4. Průsečík průměrů r, q je střed elipsy. r. . . S A k S (r, q) q. . . S

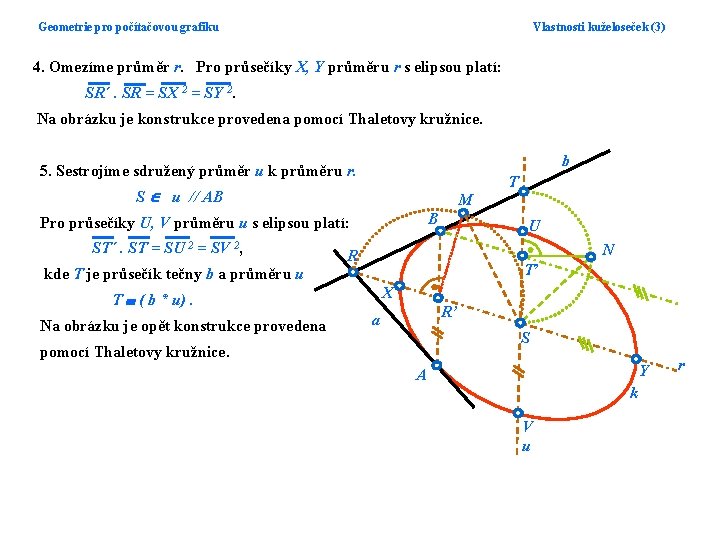
Geometrie pro počítačovou grafiku Vlastnosti kuželoseček (3) 4. Omezíme průměr r. Pro průsečíky X, Y průměru r s elipsou platí: SR´. SR = SX 2 = SY 2. Na obrázku je konstrukce provedena pomocí Thaletovy kružnice. b 5. Sestrojíme sdružený průměr u k průměru r. T S u // AB M B Pro průsečíky U, V průměru u s elipsou platí: ST´. ST = SU 2 = SV 2, U N R T’ kde T je průsečík tečny b a průměru u X T ( b * u). Na obrázku je opět konstrukce provedena R’ a S pomocí Thaletovy kružnice. Y A k V u r

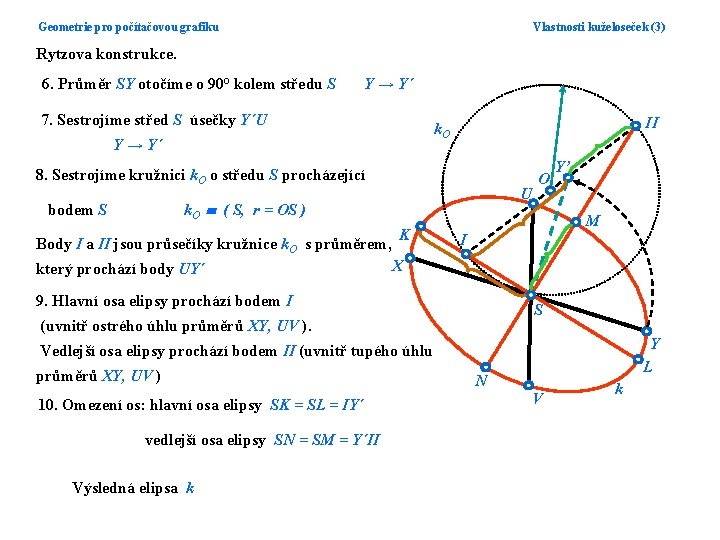
Geometrie pro počítačovou grafiku Vlastnosti kuželoseček (3) Rytzova konstrukce. 6. Průměr SY otočíme o 90° kolem středu S Y → Y´ 7. Sestrojíme střed S úsečky Y´U II k. O Y → Y´ 8. Sestrojíme kružnici k. O o středu S procházející U k. O ( S, r = OS ) bodem S Body I a II jsou průsečíky kružnice k. O s průměrem, který prochází body UY´ K O Y’ M I X 9. Hlavní osa elipsy prochází bodem I S (uvnitř ostrého úhlu průměrů XY, UV ). Y L Vedlejší osa elipsy prochází bodem II (uvnitř tupého úhlu průměrů XY, UV ) 10. Omezení os: hlavní osa elipsy SK = SL = IY´ vedlejší osa elipsy SN = SM = Y´II Výsledná elipsa k N V k

Geometrie pro počítačovou grafiku Vlastnosti kuželoseček (3) Konec