FiveMinute Check over Lesson 7 1 ThenNow New

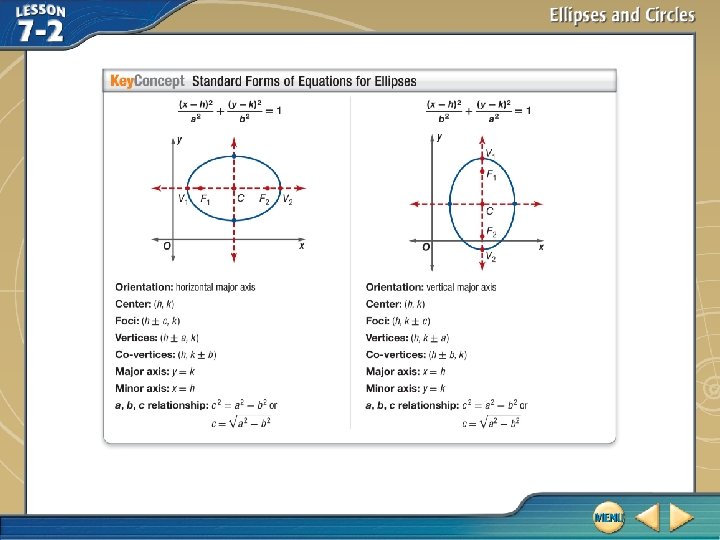
Five-Minute Check (over Lesson 7 -1) Then/Now New Vocabulary Key Concept: Standard Forms of Equations for Ellipses Example 1: Graph Ellipses Example 2: Write Equations Given Characteristics Key Concept: Eccentricity Example 3: Determine the Eccentricity of an Ellipse Example 4: Real World Example: Use Eccentricity Key Concept: Standard Form of Equations for Circles Example 5: Determine Types of Conics

Over Lesson 7 -1 Write y 2 – 6 y – 4 x + 17 = 0 in standard form. Identify the vertex, focus, axis of symmetry, and directrix. A. (y – 3)2 = 4(x – 2); vertex: (2, 3); focus: (3, 3); axis of symmetry: y = 3; directrix: x = 1 B. (y – 3)2 = 4(x – 2); vertex: (2, 3); focus: (1, 3); axis of symmetry: y = 3; directrix: x = 3 C. (y – 3)2 = 4(x – 2); vertex: (3, 2); focus: (3, 3); axis of symmetry: y = 3; directrix: x = 1 D. (y – 3)2 = 4(x – 2); vertex: (2, 3); focus: (6, 3); axis of symmetry: y = 3; directrix: x = – 2

Over Lesson 7 -1 Write x 2 + 8 x – 4 y + 8 = 0 in standard form. Identify the vertex, focus, axis of symmetry, and directrix. A. (x + 4)2 = 4(y + 2); vertex: (– 4, – 2); focus: (– 3, – 2); axis of symmetry: x = – 2; directrix: y = – 5 B. (x + 4)2 = 4(y + 2); vertex: (– 4, – 2); focus: (– 4, – 1); axis of symmetry: x = – 4; directrix: y = – 3 C. (x + 4)2 = 4(y + 2); vertex: (– 4, – 2); focus: (– 4, – 3); axis of symmetry: x = – 4; directrix: y = – 1 D. (x + 4)2 = 4(y + 2); vertex: (– 4, – 2); focus: (– 4, 2); axis of symmetry: x = – 4; directrix: y = – 6

Over Lesson 7 -1 Write an equation for a parabola with focus F (2, – 5) and vertex V (2, – 3). A. (x – 2)2 = 8(y + 5) B. (x – 2)2 = 8(y + 3) C. (x – 2)2 = 2(y + 3) D. (x – 2)2 = – 8(y + 3)

Over Lesson 7 -1 Write an equation for a parabola with focus F (2, – 2) and vertex V (– 1, – 2). A. (x – 2)2 = 12(y + 2) B. (y + 2)2 = 12(x – 2) C. (y + 2)2 = 12(x + 1) D. (x + 1)2 = 12(y + 2)

Over Lesson 7 -1 Which of the following equations represents a parabola with focus (– 3, 7) and vertex (− 3, 2)? A. (x + 3)2 = 5(y – 2) B. (y + 3)2 = 5(x – 2) C. (x + 3)2 = 20(y – 2) D. (y – 2)2 = 20(x + 3)

You analyzed and graphed parabolas. (Lesson 7– 1) • Analyze and graph equations of ellipses and circles. • Use equations to identify ellipses and circles.

• ellipse • foci • major axis • center • minor axis • vertices • co-vertices • eccentricity

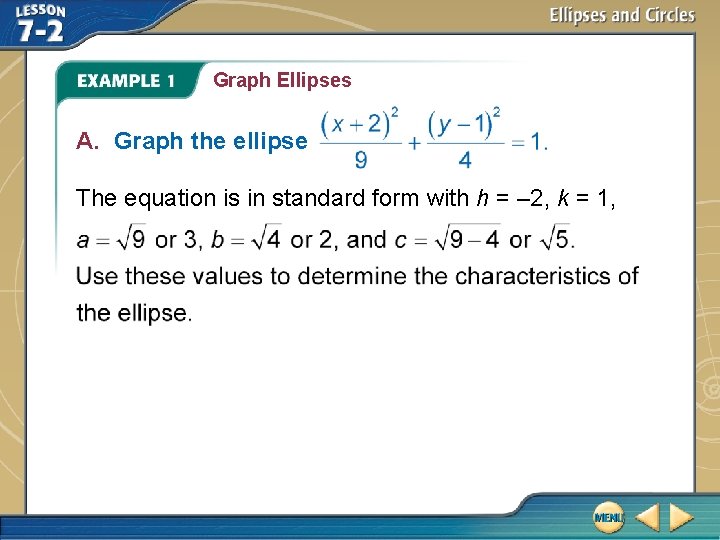
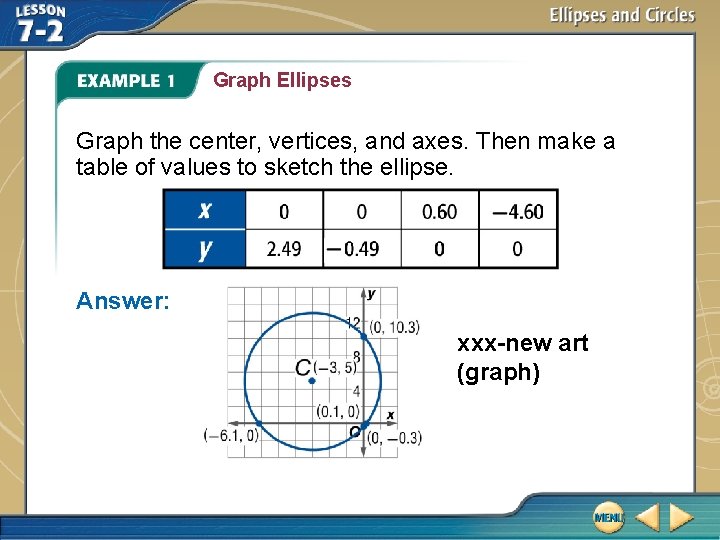
Graph Ellipses A. Graph the ellipse The equation is in standard form with h = – 2, k = 1,

Graph Ellipses

Graph Ellipses Graph the center, vertices, and axes. Then make a table of values to sketch the ellipse. Answer: xxx-new art (graph)

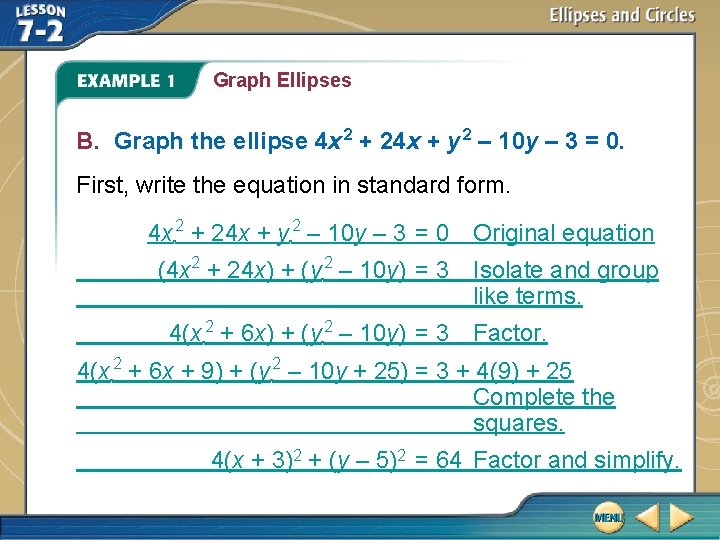
Graph Ellipses B. Graph the ellipse 4 x 2 + 24 x + y 2 – 10 y – 3 = 0. First, write the equation in standard form. 4 x 2 + 24 x + y 2 – 10 y – 3 = 0 Original equation (4 x 2 + 24 x) + (y 2 – 10 y) = 3 Isolate and group like terms. 4(x 2 + 6 x) + (y 2 – 10 y) = 3 Factor. 4(x 2 + 6 x + 9) + (y 2 – 10 y + 25) = 3 + 4(9) + 25 Complete the squares. 4(x + 3)2 + (y – 5)2 = 64 Factor and simplify.

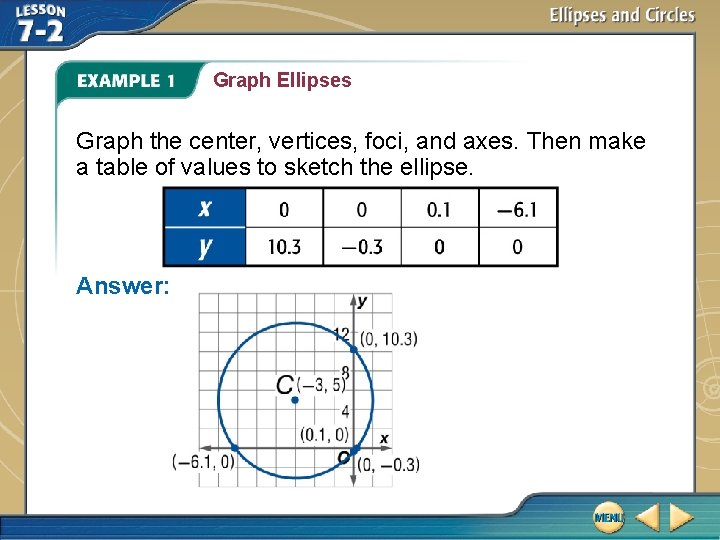
Graph Ellipses Divide each side by 64.

Graph Ellipses

Graph Ellipses Graph the center, vertices, foci, and axes. Then make a table of values to sketch the ellipse. Answer:

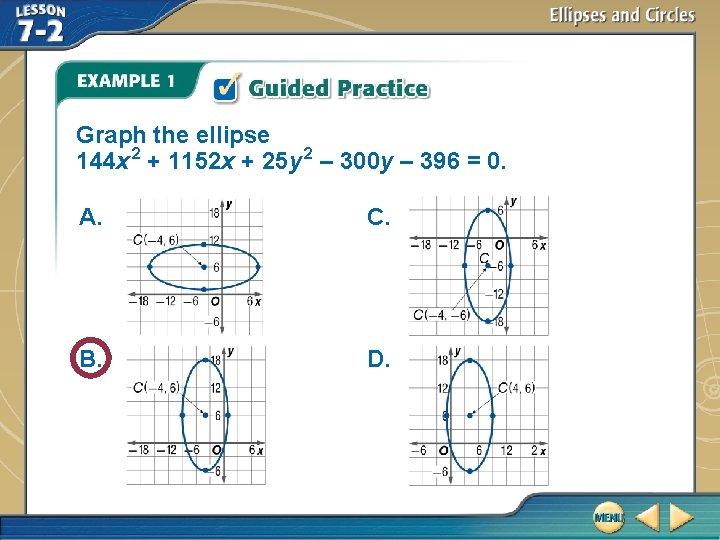
Graph the ellipse 144 x 2 + 1152 x + 25 y 2 – 300 y – 396 = 0. A. C. B. D.

Write Equations Given Characteristics A. Write an equation for an ellipse with a major axis from (5, – 2) to (– 1, – 2) and a minor axis from (2, 0) to (2, – 4). Use the major and minor axes to determine a and b. Half the length of major axis Half the length of minor axis The center of the ellipse is at the midpoint of the major axis.

Write Equations Given Characteristics Midpoint formula = (2, – 2) Simplify. The y-coordinates are the same for both endpoints of the major axis, so the major axis is horizontal and the value of a belongs with the x 2 -term. An equation for the ellipse is . Answer:

Write Equations Given Characteristics B. Write an equation for an ellipse with vertices at (3, – 4) and (3, 6) and foci at (3, 4) and (3, – 2) The length of the major axis, 2 a, is the distance between the vertices. Distance formula a = 5 Simplify.

Write Equations Given Characteristics 2 c represents the distance between the foci. Distance formula c = 3 Simplify. Find the value of b. c 2 = a 2 – b 2 Equation relating a, b, and c 32 = 52 – b 2 a = 5 and c = 3 b = 4 Simplify.

Write Equations Given Characteristics The vertices are equidistant from the center. Midpoint formula = (3, 1) Simplify. The x-coordinates are the same for both endpoints of the major axis, so the major axis is vertical and the value of a belongs with the y 2 -term. An equation for the ellipse is

Write Equations Given Characteristics Answer:

Write an equation for an ellipse with co-vertices (– 8, 6) and (4, 6) and major axis of length 18. A. B. C. D.

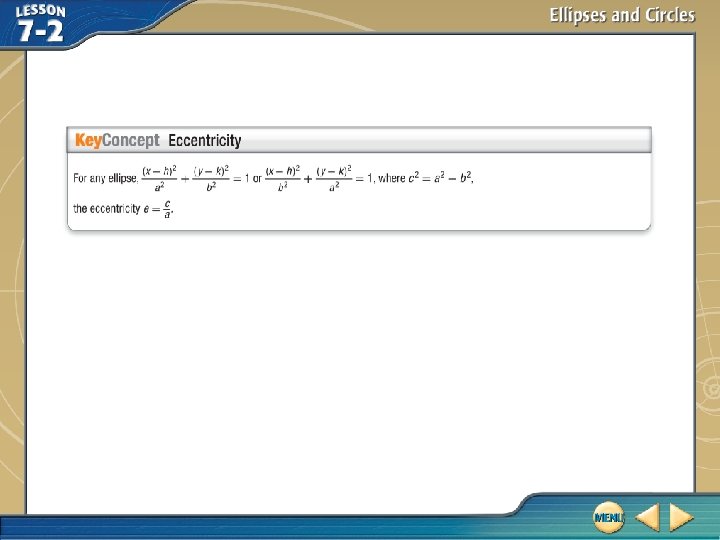
Determine the Eccentricity of an Ellipse Determine the eccentricity of the ellipse given by First, determine the value of c. c 2 = a 2 – b 2 Equation relating a, b, and c c 2 = 64 – 36 a 2 = 64 and b 2 = 36 c = Simplify.

Determine the Eccentricity of an Ellipse Use the values of c and a to find the eccentricity. Eccentricity equation a = 8 The eccentricity of the ellipse is about 0. 66. Answer: about 0. 66

Determine the eccentricity of the ellipse given by 36 x 2 + 144 x + 49 y 2 – 98 y = 1571. A. 0. 27 B. 0. 36 C. 0. 52 D. 0. 60

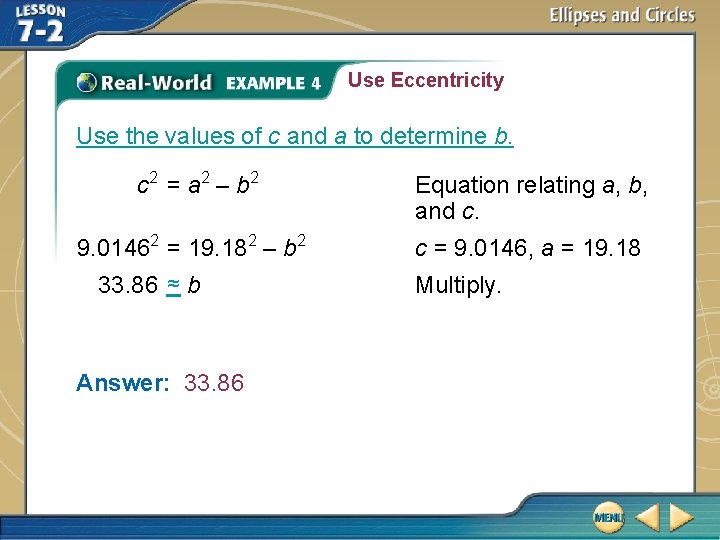
Use Eccentricity ASTRONOMY The eccentricity of the orbit of Uranus is 0. 47. Its orbit around the Sun has a major axis length of 38. 36 AU (astronomical units). What is the length of the minor axis of the orbit? The major axis is 38. 36, so a = 19. 18. Use the eccentricity to find the value of c. Definition of eccentricity e = 0. 47, a = 19. 18 9. 0146 = c Multiply.

Use Eccentricity Use the values of c and a to determine b. c 2 = a 2 – b 2 Equation relating a, b, and c. 9. 01462 = 19. 182 – b 2 c = 9. 0146, a = 19. 18 33. 86 ≈ b Answer: 33. 86 Multiply.

PARKS A lake in a park is elliptically-shaped. If the length of the lake is 2500 meters and the width is 1500 meters, find the eccentricity of the lake. A. 0. 2 B. 0. 4 C. 0. 6 D. 0. 8

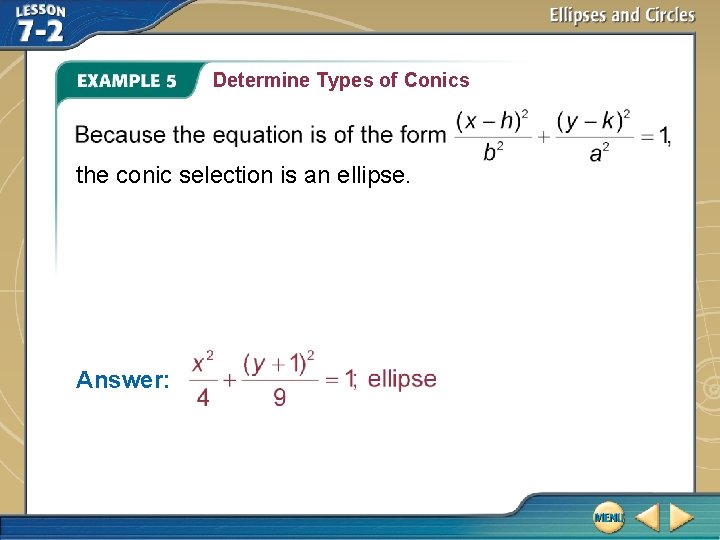
Determine Types of Conics A. Write 9 x 2 + 4 y 2 + 8 y – 32 = 0 in standard form. Identify the related conic. 9 x 2 + 4 y 2 + 8 y – 32 = 0 Original equation 9 x 2 + 4(y 2 + 2 y)= 32 Isolate like terms. 9 x 2 + 4(y 2 + 2 y + 1) = 32 + 4(1) Complete the square. 9 x 2 + 4(y + 1)2 = 36 Factor and simplify. Divide each side by 36.

Determine Types of Conics the conic selection is an ellipse. Answer:

Determine Types of Conics B. Write x 2 + 4 x – 4 y + 16 = 0 in standard form. Identify the related conic selection. x 2 + 4 x – 4 y + 16 = 0 x 2 + 4 x + 4 – 4 y + 16 = 0 + 4 (x + 2)2 – 4 y + 16 = 4 Original equation Complete the square. Factor and simplify. (x + 2)2 = 4 y – 12 Add 4 y – 16 to each side. (x + 2)2 = 4(y – 3) Factor. Because only one term is squared, the conic selection is a parabola. Answer: (x + 2)2 = 4(y – 3); parabola

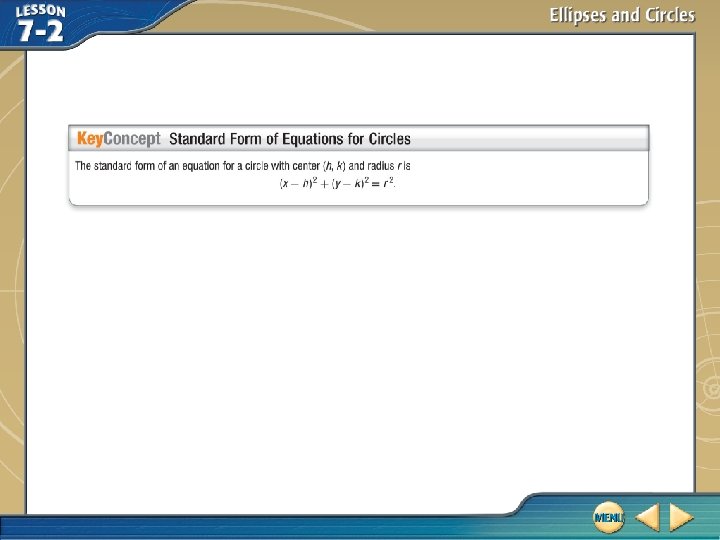
Determine Types of Conics C. Write x 2 + y 2 + 2 x – 6 y – 6 = 0 in standard form. Identify the related conic. x 2 + y 2 + 2 x – 6 y – 6 = 0 Original equation x 2 + 2 x + y 2 – 6 y = 6 Isolate like terms. x 2 + 2 x + 1 + y 2 – 6 y + 9 = 6 + 1 + 9 (x + 1)2 + (y – 3)2 = 16 Complete the square. Factor and simplify. Because the equation is of the form (x – h)2 + (y – k)2 = r 2, the conic selection is a circle. Answer: (x + 1)2 + (y – 3)2 = 16; circle

Write 16 x 2 + y 2 + 4 y – 60 = 0 in standard form. Identify the related conic. A. B. 16 x 2 + (y + 2)2 = 64; circle C. D. 16 x 2 + (y + 2)2 = 64; ellipse