ECO 290 E Game Theory Lecture 5 Mixed

ECO 290 E: Game Theory Lecture 5 Mixed Strategy Equilibrium

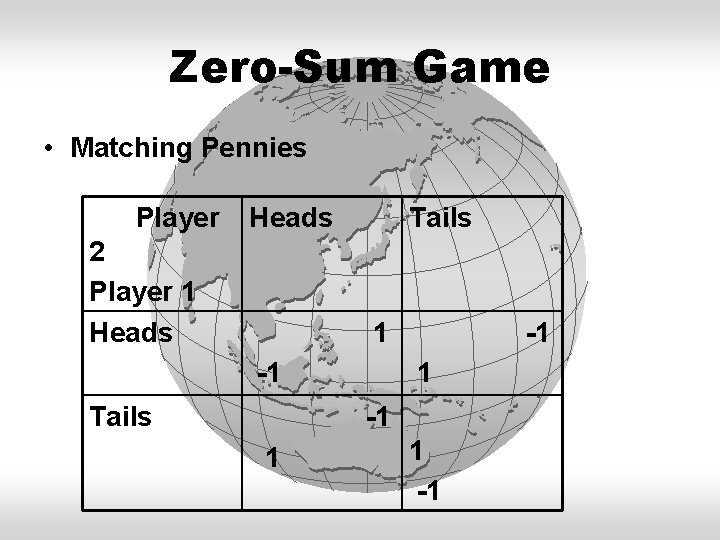
Zero-Sum Game • Matching Pennies Player Heads 2 Player 1 Heads Tails 1 -1 Tails -1 1 1 -1

No Nash Equilibrium? • The distinguishing feature of zero-sum game is that each player would like to outguess the other since there is no “win-win” situation. • Example: Porker (bluff or not), Battle (by land or by sea), Tennis (left or right to serve) • When each player would always like outguess the other(s), there is no Nash equilibrium. Þ Contradicting Nash’s theorem? ?

Mixed Strategy • A mixed strategy for a player is a probability distribution over some (or all) of her strategies. • The strategy we have studied so far, i. e. , taking some action for sure, is called a purestrategy. • When the outcome of the game is uncertain, we assume that each player maximizes expected value of her payoff. Þ Expected utility theory (von Neumann and Morgenstern, 1944)

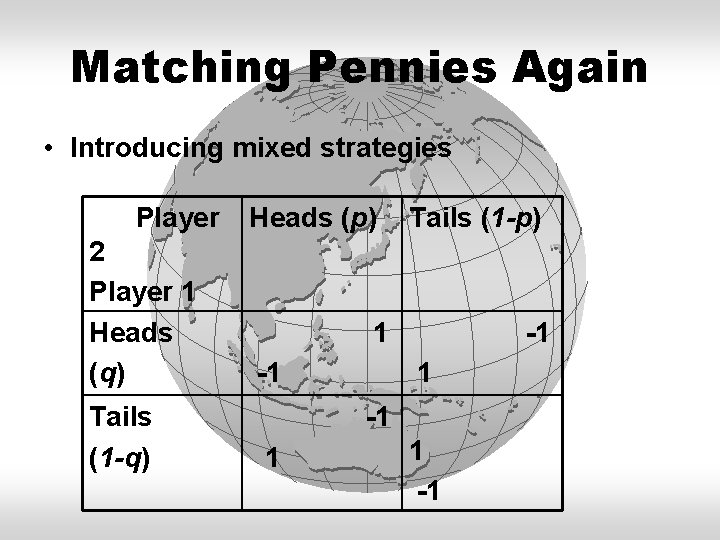
Matching Pennies Again • Introducing mixed strategies Player 2 Player 1 Heads (q) Tails (1 -q) Heads (p) Tails (1 -p) 1 -1 -1 1 1 -1

How to Find Equilibrium? • If a player takes both “Heads” and “Tails” with positive probability, she must be indifferent between these two pure strategies, i. e. , the expected payoff derived by choosing Heads must be equal to that by choosing Tails. • -p+(1 -p)=p-(1 -p), hence p=0. 5. • q-(1 -q)=-q+(1 -q), hence q=0. 5.

How to Verify Equilibrium? • Note that if p=0. 5, Player 1 does not have a strict incentive to change her strategy from q=0. 5. • Similarly, Player 2 does not have a strict incentive to change his strategy from p=0. 5, if q=0. 5. Þ Therefore, p=q=0. 5 constitutes a mixedstrategy equilibrium. Q: Is this equilibrium reasonable/stable? A: Yes (each player ends up randomizing two strategies equally if the rival is smart enough).

Modified Matching Pennies • Suppose the payoffs in the up-left cell changes as the following: Player 2 Heads (p) Player 1 Heads (q) Tails (1 -p) 2 -2 -1 1 1 -1

Indifference Property • Under mixed-strategy NE, Player 1 must be indifferent between choosing H and T: Þ -2 p+(1 -p)=p-(1 -p), hence p=0. 4. • Similarly, Player 2 must be indifferent between choosing H and T: Þ 2 q-(1 -q)=-q+(1 -q), hence q=0. 4. • You can easily verify that (p, q)=(0. 4, 0. 4) indeed becomes a mixed-strategy NE.

Existence of NE Theorem (Nash, 1950) • If a game has finite number of players and actions, then there exists at least one Nash equilibrium, possibly involving mixed strategies. Þ The proof uses the Kakutani’s fixed-point theorem. Þ Best response mappings satisfy the condition of the fixed-point theorem, and hence have a fixed point, which is equivalent to a NE!

Infinite Games • The finite game assumption is not necessary but gives a sufficient condition for the existence of NE. • There are many games that do not satisfy the conditions of the Theorem but nonetheless have one or more NE. (e. g. , Bertrand model, Cournot model) Q: Are there any games which do not even have a mixed-strategy equilibrium? A: Yes, e. g. , Integer game.

Reporting a Crime • A crime is observed by a group of n people. Each person would like the police to be informed but prefers that someone else make the phone call. • Players: The n people. • Strategies: “Call” or “Don’t call” • Payoffs: 0 if no one calls. v if someone else calls but she does not. v-c if the player calls.

Pure-Strategy Equilibrium • This game has n pure-strategy NE, in each of which exactly one person calls. (if that person switches to not calling, her payoff falls from v-c to 0; if any other person switches to calling, his payoff falls from v to v-c. ) • If the members of the group differ in some respect, then these asymmetric equilibria may be compelling as steady states. • For example, the social norm in which the oldest person in the group makes the phone call is stable.

Mixed-Strategy Equilibrium • There is a symmetric mixed strategy equilibrium in which each person calls with positive probability p<1. • In any such equilibrium, each person’s expected payoff to calling is equal to her expected payoff to not calling. Þ v-c=v(1 -Pr{no one else calls}) Þ c/v=Pr{no one else calls} • Notice that the probability that no one else calls is independent of n, but constant!

Implication Pr{no one calls} =Pr{i does not call}x. Pr{no one else calls} =(1 -p)c/v • You can show that 1 -p is increasing in n, i. e. , the probability that person i does not call increases as n becomes larger. • This implies that the probability that no one calls is also increasing in n. Þ The larger the group, the less likely the police are informed of the crime!