Determination of Grain Boundary Stiffness Hao Zhang 1

Determination of Grain Boundary Stiffness Hao Zhang 1, Mikhail Mendelev 1, 2 and David Srolovitz 1 1 PRISM, Princeton University 2 Ames Laboratory
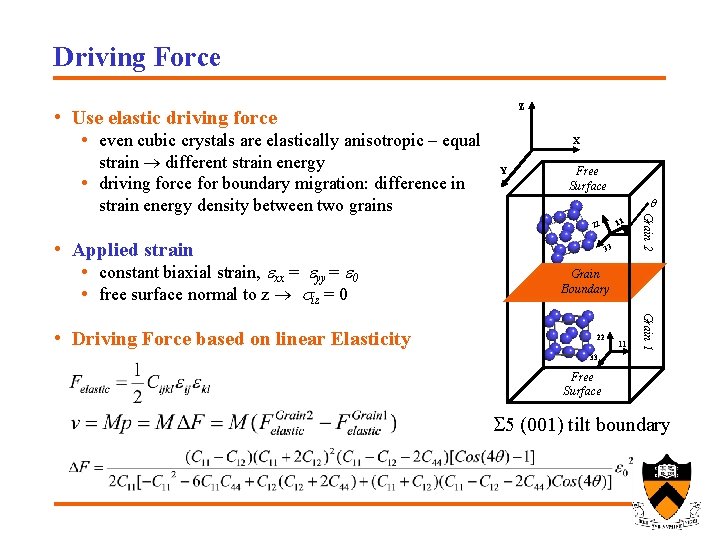
Driving Force Z • Use elastic driving force • even cubic crystals are elastically anisotropic – equal Y Free Surface q 11 22 • Applied strain • constant biaxial strain, exx = eyy = e 0 • free surface normal to z iz = 0 Grain Boundary 22 11 Grain 1 • Driving Force based on linear Elasticity 33 Grain 2 strain different strain energy • driving force for boundary migration: difference in strain energy density between two grains X 33 Free Surface S 5 (001) tilt boundary
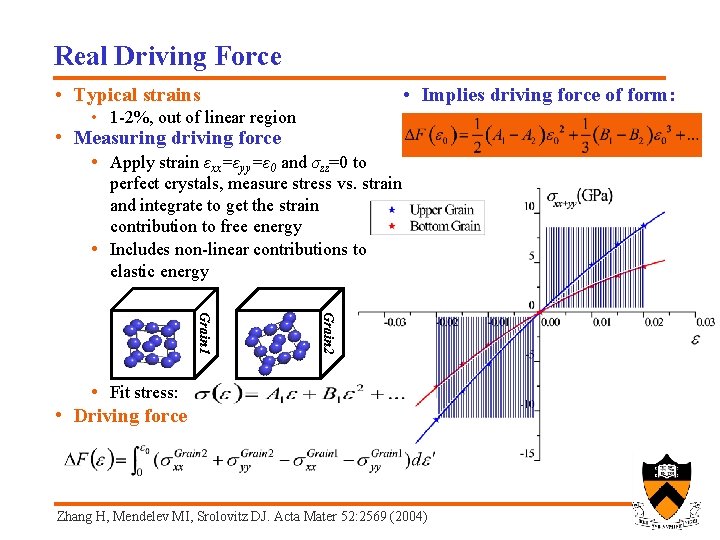
Real Driving Force • Typical strains • Implies driving force of form: • 1 -2%, out of linear region • Measuring driving force • Apply strain εxx=εyy=ε 0 and σzz=0 to perfect crystals, measure stress vs. strain and integrate to get the strain contribution to free energy • Includes non-linear contributions to elastic energy Grain 2 Grain 1 • Fit stress: • Driving force Zhang H, Mendelev MI, Srolovitz DJ. Acta Mater 52: 2569 (2004)
![Simulation / Bicrystal Geometry [010] S 5 36. 87º a a Asymmetric boundary a Simulation / Bicrystal Geometry [010] S 5 36. 87º a a Asymmetric boundary a](http://slidetodoc.com/presentation_image_h/37fd9ef808242def9ea8db38a90acd5e/image-4.jpg)
Simulation / Bicrystal Geometry [010] S 5 36. 87º a a Asymmetric boundary a = 26. 57º Asymmetric boundary a = 14. 04º Symmetric boundary

Initial Simulation Cell for Different Inclinations
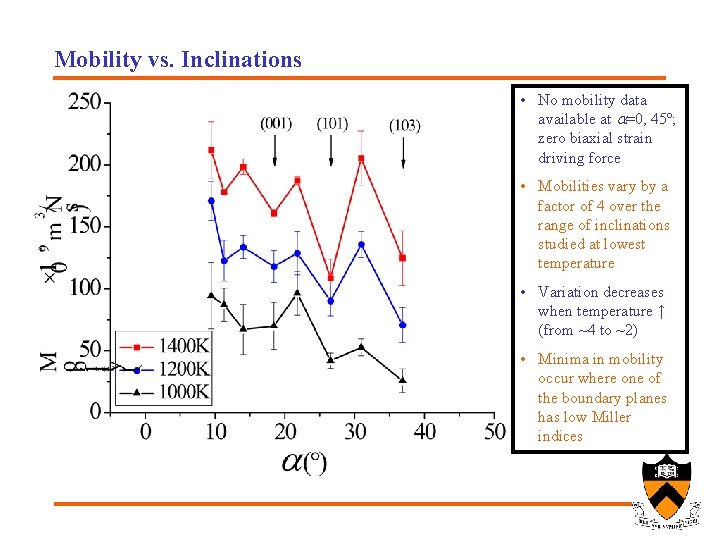
Mobility vs. Inclinations • No mobility data available at a=0, 45º; zero biaxial strain driving force • Mobilities vary by a factor of 4 over the range of inclinations studied at lowest temperature • Variation decreases when temperature ↑ (from ~4 to ~2) • Minima in mobility occur where one of the boundary planes has low Miller indices
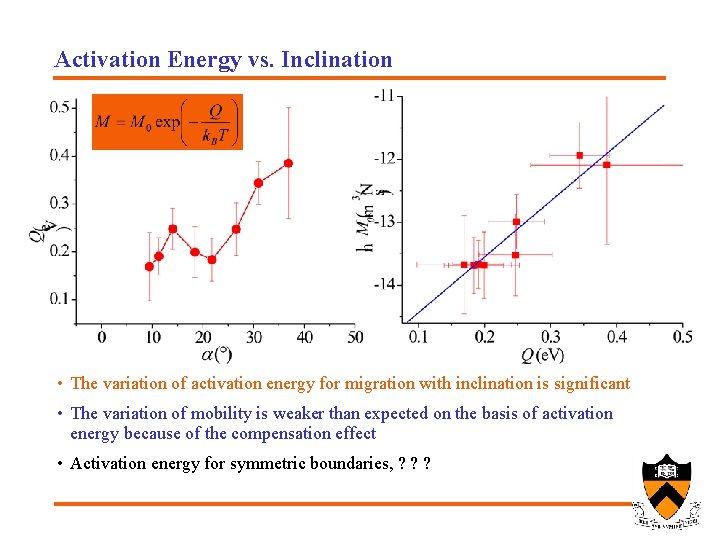
Activation Energy vs. Inclination • The variation of activation energy for migration with inclination is significant • The variation of mobility is weaker than expected on the basis of activation energy because of the compensation effect • Activation energy for symmetric boundaries, ? ? ?

Determination of Grain Boundary Stiffness • Determine reduced mobility from simulation of shrinking, grain • Capillarity driven migration <01 0> <10 0> • Radial velocity for arbitrary curve <010> <100> r n a O q

Determination of Grain Boundary Stiffness (Contd) • If grain shape is only slightly different from a circle, we can assume 4 -fold symmetry - [010] tilt • Substituting into expression for the velocity and rearranging terms r • Keep the first order terms n a O q • To find how the reduced mobility varies with inclination, a, we must relate a to q

Circular Shrinkage Geometry
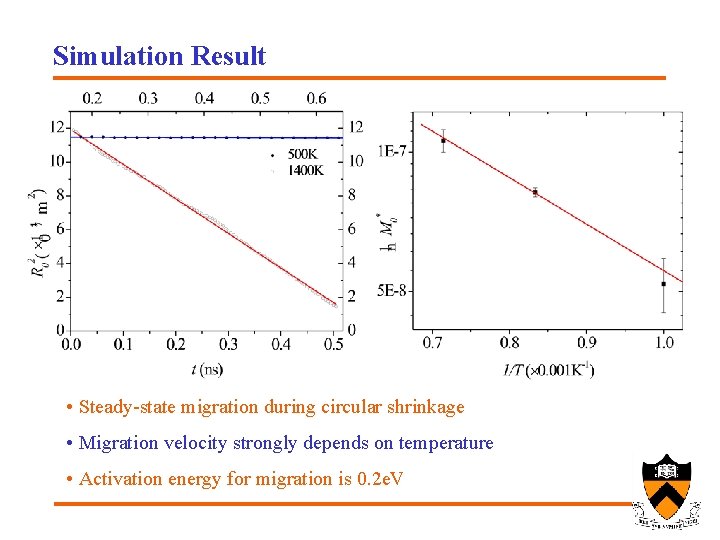
Simulation Result • Steady-state migration during circular shrinkage • Migration velocity strongly depends on temperature • Activation energy for migration is 0. 2 e. V
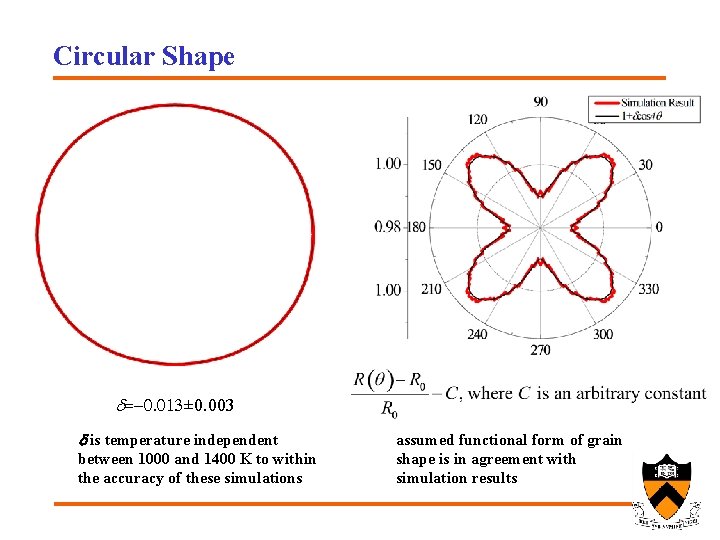
Circular Shape d=-0. 013± 0. 003 d is temperature independent between 1000 and 1400 K to within the accuracy of these simulations assumed functional form of grain shape is in agreement with simulation results
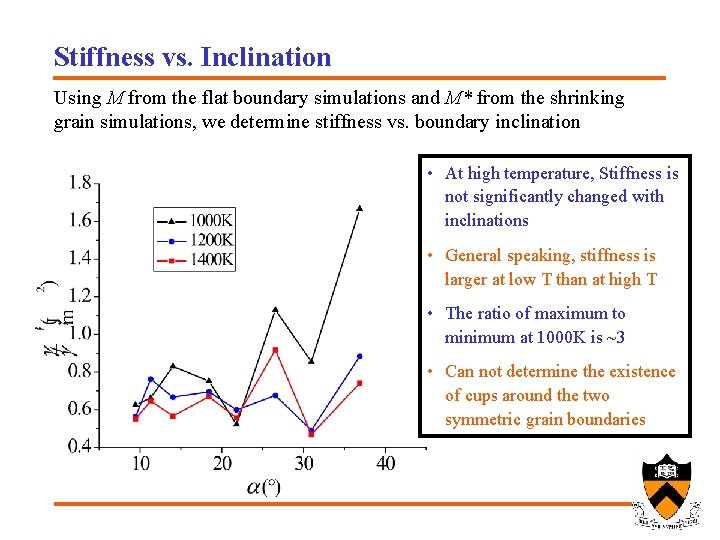
Stiffness vs. Inclination Using M from the flat boundary simulations and M* from the shrinking grain simulations, we determine stiffness vs. boundary inclination • At high temperature, Stiffness is not significantly changed with inclinations • General speaking, stiffness is larger at low T than at high T • The ratio of maximum to minimum at 1000 K is ~3 • Can not determine the existence of cups around the two symmetric grain boundaries

Conclusion • Developed new method (stress driven GB motion) to determine grain boundary mobility as a function of q, a and T • Extracted grain boundary stiffness from atomistic simulations • Mobility is a strong function of inclination and temperature; mobility exhibits minima where at least one of the boundary planes has low Miller indices • Grain boundary stiffness varies with inclination and is only weakly temperature-dependent
- Slides: 14