Curved spaces Picture a smooth surface Spaces like


- Slides: 14

Curved spaces Picture a smooth surface: Spaces like this, where there are no kinks, are called manifolds. They can have any dimension.

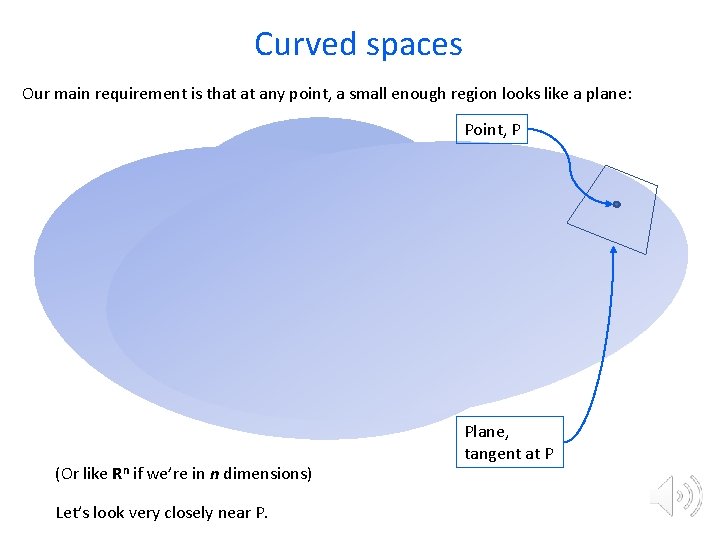
Curved spaces Our main requirement is that at any point, a small enough region looks like a plane: Point, P (Or like Rn if we’re in n dimensions) Let’s look very closely near P. Plane, tangent at P

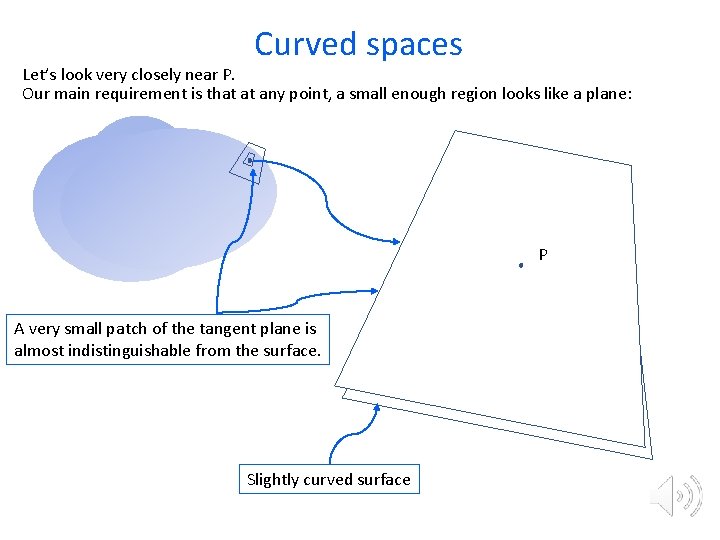
Curved spaces Let’s look very closely near P. Our main requirement is that at any point, a small enough region looks like a plane: P A very small patch of the tangent plane is almost indistinguishable from the surface. Slightly curved surface

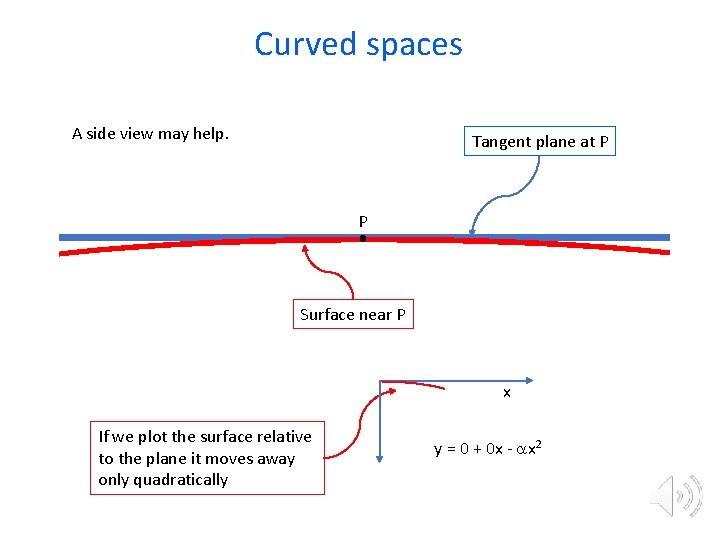
Curved spaces A side view may help. Tangent plane at P P Surface near P x If we plot the surface relative to the plane it moves away only quadratically y = 0 + 0 x - ax 2

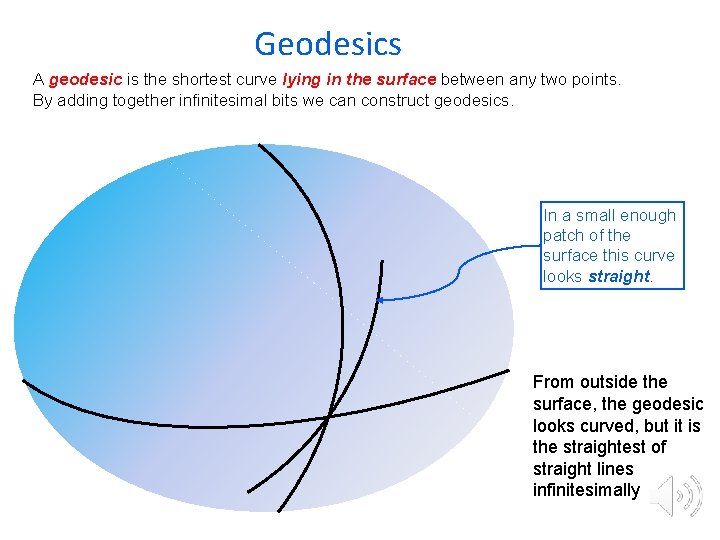
Geodesics A geodesic is the shortest curve lying in the surface between any two points. By adding together infinitesimal bits we can construct geodesics. In a small enough patch of the surface this curve looks straight. From outside the surface, the geodesic looks curved, but it is the straightest of straight lines infinitesimally

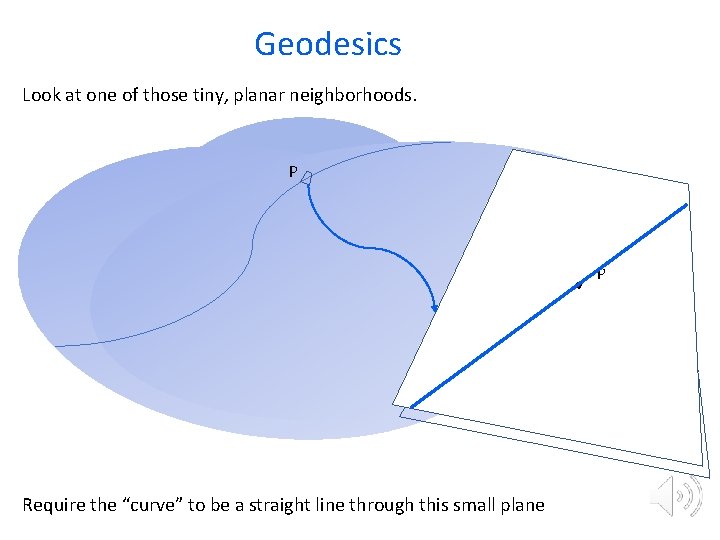
Geodesics On our smooth surface, draw a smooth curve. We want to make this curve as straight as possible while keeping it on the surface.

Geodesics Look at one of those tiny, planar neighborhoods. P P Require the “curve” to be a straight line through this small plane

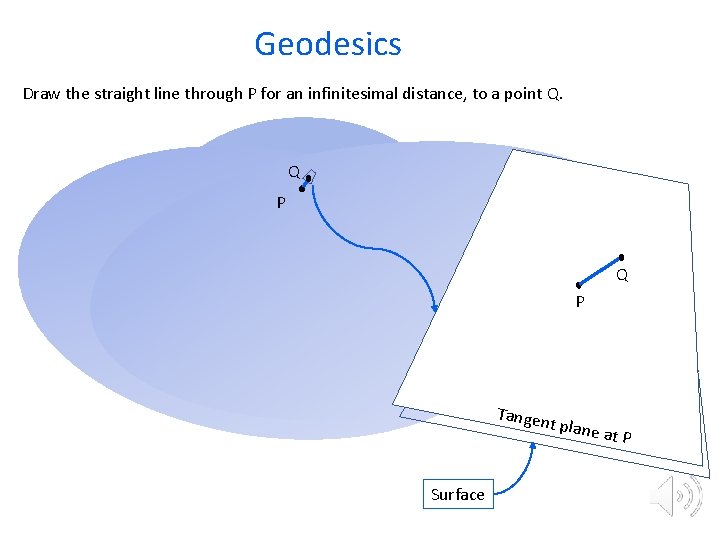
Geodesics Draw the straight line through P for an infinitesimal distance, to a point Q. Q P Tangen t plane Surface at P

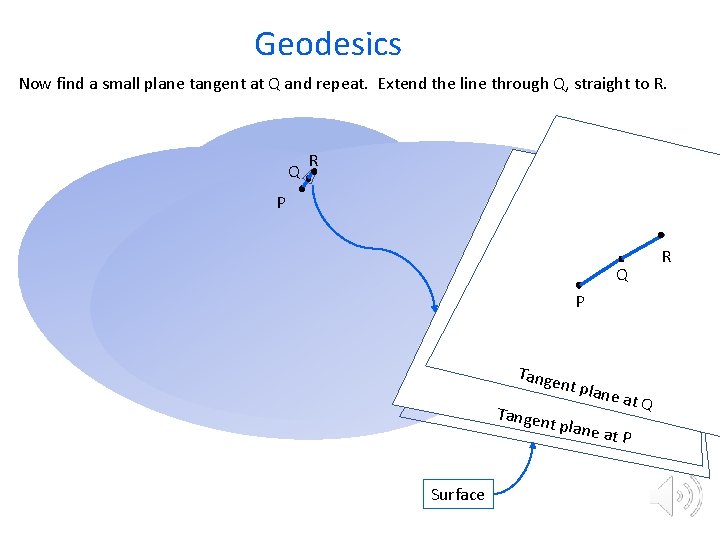
Geodesics Now find a small plane tangent at Q and repeat. Extend the line through Q, straight to R. Q R P Q P Tange nt pla ne at Q Tangen t plane at P Surface R

Geodesics As long as we carry out the process infinitesimally, we get a smooth curve across the surface. This “straightest possible curve” is a geodesic

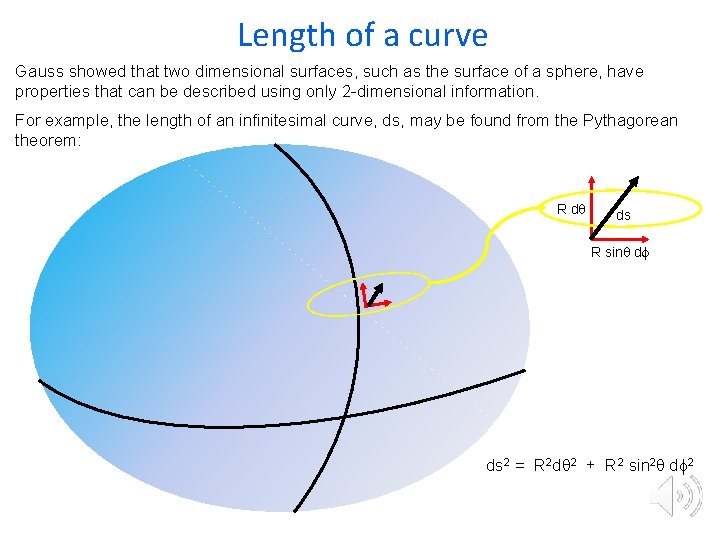
Length of a curve Gauss showed that two dimensional surfaces, such as the surface of a sphere, have properties that can be described using only 2 -dimensional information. For example, the length of an infinitesimal curve, ds, may be found from the Pythagorean theorem: R dq ds R sinq df ds 2 = R 2 dq 2 + R 2 sin 2 q df 2

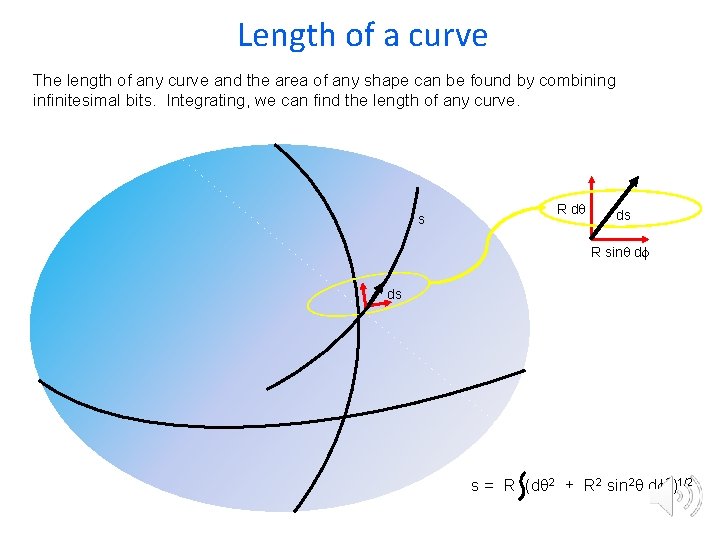
Length of a curve The length of any curve and the area of any shape can be found by combining infinitesimal bits. Integrating, we can find the length of any curve. s R dq ds R sinq df ds s = R (dq 2 + R 2 sin 2 q df 2)1/2

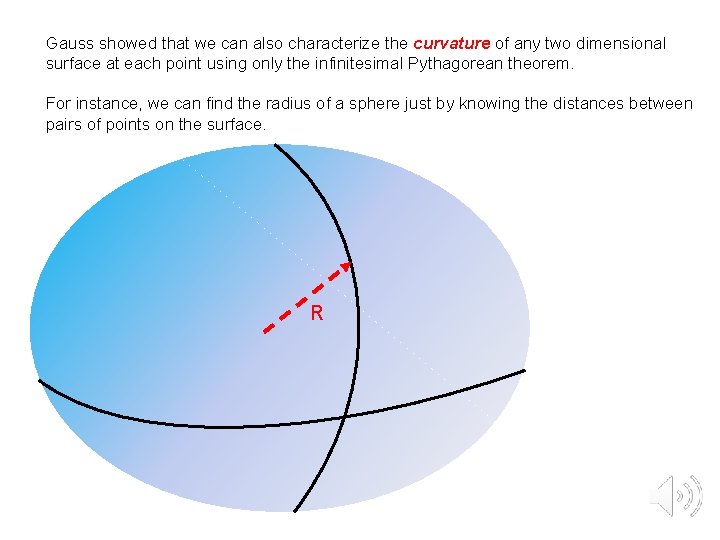
Gauss showed that we can also characterize the curvature of any two dimensional surface at each point using only the infinitesimal Pythagorean theorem. For instance, we can find the radius of a sphere just by knowing the distances between pairs of points on the surface. R

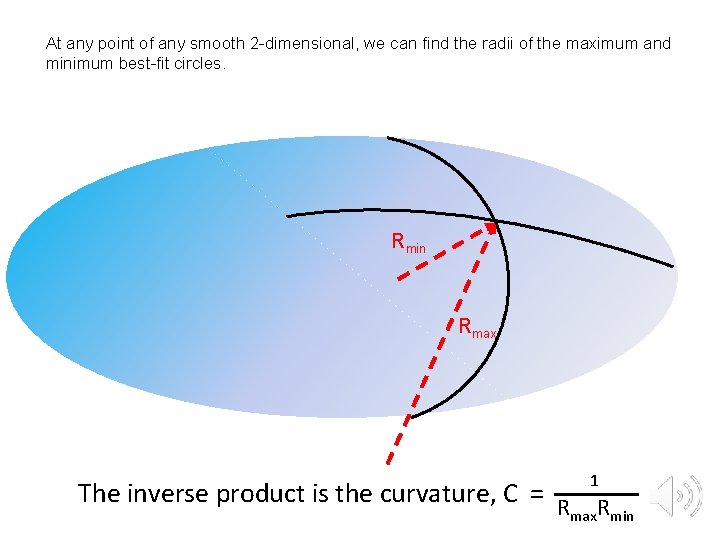
At any point of any smooth 2 -dimensional, we can find the radii of the maximum and minimum best-fit circles. Rmin Rmax 1 The inverse product is the curvature, C = R R max min
 Curved surface area and total surface area of cone
Curved surface area and total surface area of cone Surface area of pyramids and cones
Surface area of pyramids and cones Circular surface area of cylinder
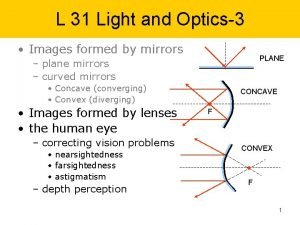
Circular surface area of cylinder Why does light not bend when it hits a curved surface
Why does light not bend when it hits a curved surface Single curved surface
Single curved surface 6 rectangular faces 8 vertices 12 edges
6 rectangular faces 8 vertices 12 edges Hemisphere surface area
Hemisphere surface area What is lateral area
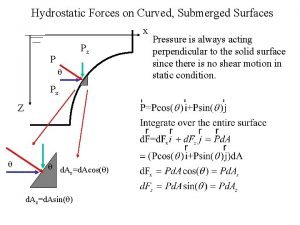
What is lateral area Submerged curved surface
Submerged curved surface Hydrostatic force on curved surface
Hydrostatic force on curved surface Zones of dentinal caries
Zones of dentinal caries Katherine arden md
Katherine arden md Picture 1 picture 2
Picture 1 picture 2 Lateral surface area of a prism formula
Lateral surface area of a prism formula High surface tension vs low surface tension
High surface tension vs low surface tension