CSE 5311 DESIGN AND ANALYSIS OF ALGORITHMS Definitions

CSE 5311 DESIGN AND ANALYSIS OF ALGORITHMS

Definitions of Algorithm n n n A mathematical relation between an observed quantity and a variable used in a step-by-step mathematical process to calculate a quantity Algorithm is any well defined computational procedure that takes some value or set of values as input and produces some value or set of values as output A procedure for solving a mathematical problem in a finite number of steps that frequently involves repetition of an operation; broadly : a step-by-step procedure for solving a problem or accomplishing some end (Webster’s Dictionary)

Analysis of Algorithms Involves evaluating the following parameters n Memory – Unit generalized as “WORDS” n Computer time – Unit generalized as “CYCLES” n Correctness – Producing the desired output

Sample Algorithm FINDING LARGEST NUMBER INPUT: unsorted array ‘A[n]’of n numbers OUTPUT: largest number -----------------------------1 large ← A[j] 2 for j ← 2 to length[A] 3 if large < A[j] 4 large ← A[j] 5 end

Space and Time Analysis (Largest Number Scan Algorithm) SPACE S(n): One “word” is required to run the algorithm (step 1…to store variable ‘large’) TIME T(n): n-1 comparisons are required to find the largest (every comparison takes one cycle) *Aim is to reduce both T(n) and S(n)

ASYMPTOTICS Used to formalize that an algorithm has running time or storage requirements that are ``never more than, '' ``always greater than, '' or ``exactly'' some amount

ASYMPTOTICS NOTATIONS O-notation (Big Oh) n n Asymptotic Upper Bound For a given function g(n), we denote O(g(n)) as the set of functions: O(g(n)) = { f(n)| there exists positive constants c and n 0 such that 0 ≤ f(n) ≤ c g(n) for all n ≥ n 0 }

ASYMPTOTICS NOTATIONS Θ-notation Asymptotic tight bound n Θ (g(n)) represents a set of functions such that: Θ (g(n)) = {f(n): there exist positive constants c 1, c 2, and n 0 such that 0 ≤ c 1 g(n) ≤ f(n) ≤ c 2 g(n) for all n≥ n 0} n

ASYMPTOTICS NOTATIONS Ω-notation Asymptotic lower bound n Ω (g(n)) represents a set of functions such that: Ω(g(n)) = {f(n): there exist positive constants c and n 0 such that 0 ≤ c g(n) ≤ f(n) for all n≥ n 0} n

n O-notation --------- Less than equal to (“≤”) n Θ-notation --------- Equal to (“=“) n Ω-notation --------- Greater than equal to (“≥”)

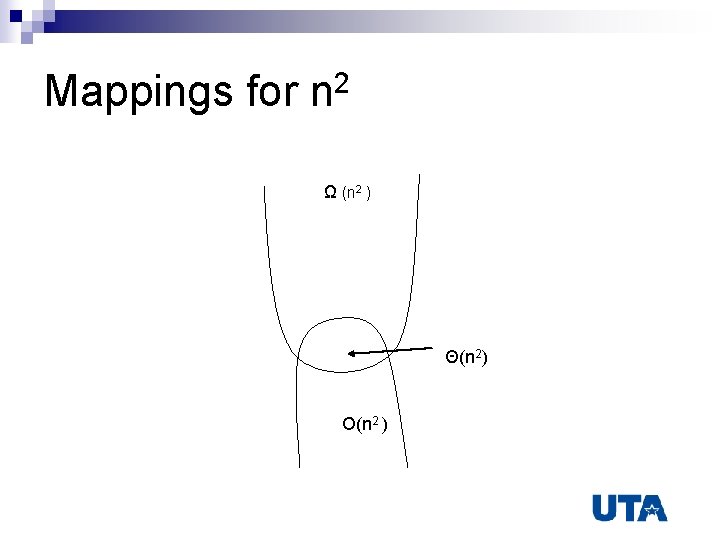
Mappings for n 2 Ω (n 2 ) Θ(n 2) O(n 2 )

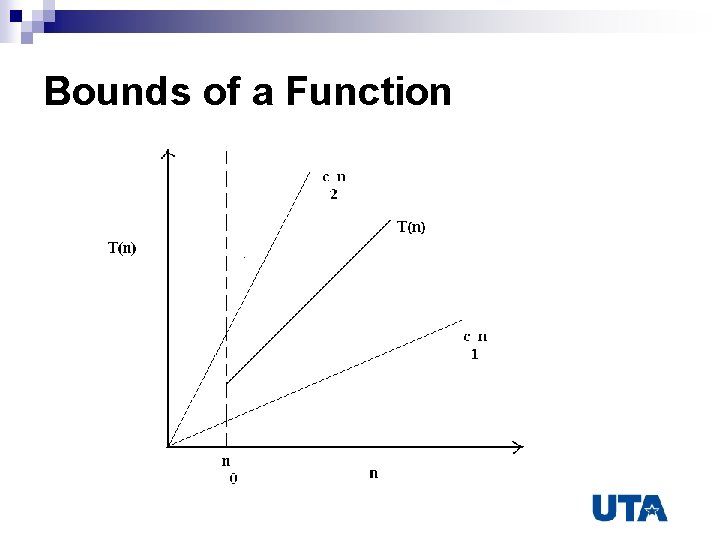
Bounds of a Function Cntd…

Cntd… c 1 , c 2 & n 0 -> constants n T(n) exists between c 1 n & c 2 n n Below n 0 we do not plot T(n) n T(n) becomes significant only above n 0 n

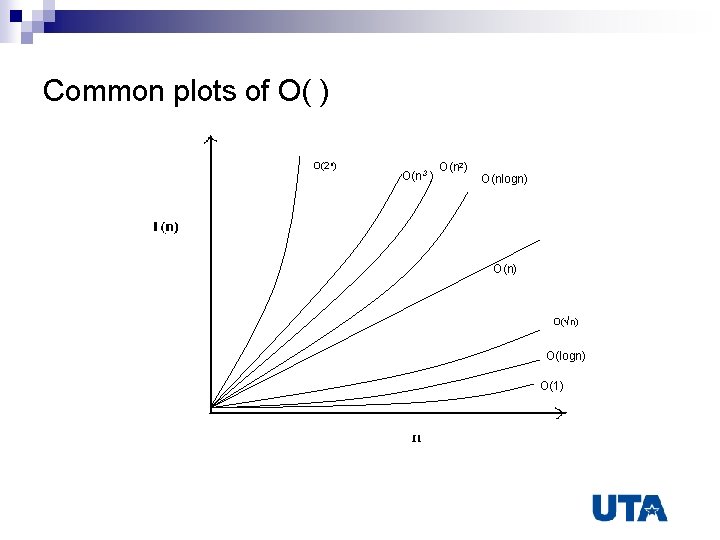
Common plots of O( ) O(2 n) O(n 3 ) O(n 2) O(nlogn) O(√n) O(logn) O(1)

Examples of algorithms for sorting techniques and their complexities Insertion sort : O(n 2) n Selection sort : O(n 2) n Quick sort : O(n logn) n Merge sort : O(n logn) n

RECURRENCE RELATIONS A Recurrence is an equation or inequality that describes a function in terms of its value on smaller inputs n Special techniques are required to analyze the space and time required n

RECURRENCE RELATIONS EXAMPLE 1: QUICK SORT T(n)= 2 T(n/2) + O(n) T(1)= O(1) n In the above case the presence of function of T on both sides of the equation signifies the presence of recurrence relation n (SUBSTITUTION MEATHOD used) The equations are simplified to produce the final result: ……cntd

Cntd…. T(n) = 2 T(n/2) + O(n) = 2(2(n/22) + (n/2)) + n = 22 T(n/22) + n = 22 (T(n/23)+ (n/22)) + n = 23 T(n/23) + n + n = n log n

Cntd… EXAMPLE 2: BINARY SEARCH T(n)=O(1) + T(n/2) T(1)=1 Above is another example of recurrence relation and the way to solve it is by Substitution. T(n)=T(n/2) +1 = T(n/22)+1+1 = T(n/23)+1+1+1 = logn T(n)= O(logn)