Chapter 8 Channel Capacity Channel Capacity Define C



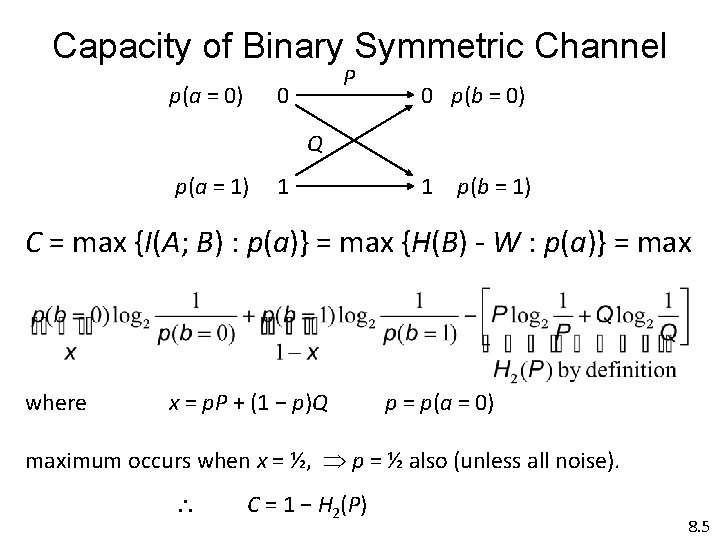

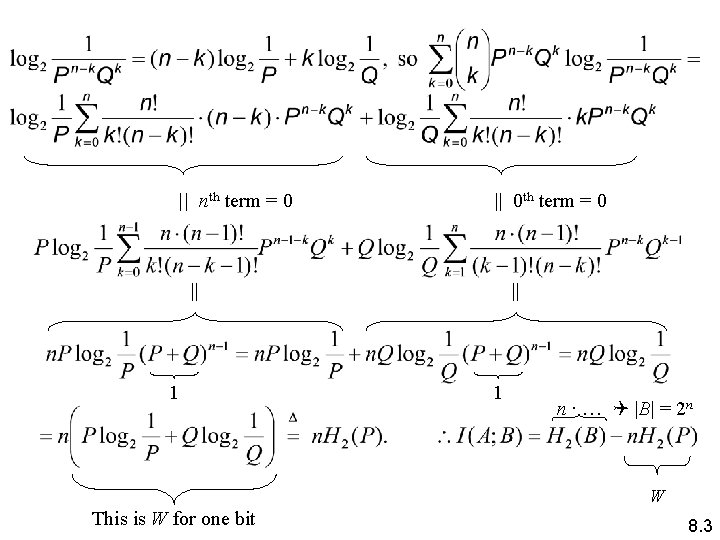

- Slides: 9

Chapter 8 Channel Capacity

Channel Capacity Define C = max {I(A; B) : p(a)} = Amount of useful information per bits actually sent = The change in entropy by going through the channel (drop in uncertainty) average uncertainty being sent: before receiving after receiving 8. 1

Uniform Channel channel probabilities do not change from symbol to symbol I. e. the rows of the probability matrix are permutations of each other. So the following is independent of a: 1 for some b Consider no noise: P(b | a) = W = 0 0 all others (conforms to intuition only if I(A ; B) = H(A) All noise implies H(B) = W permutation matrix) 8. 2
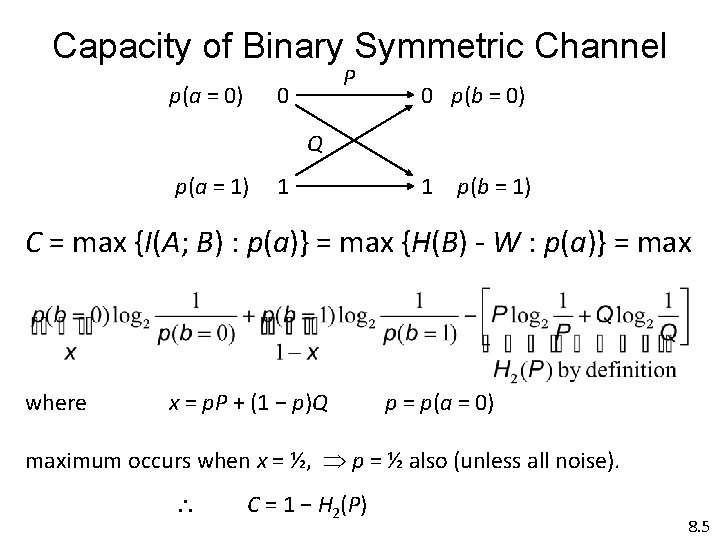
Capacity of Binary Symmetric Channel p(a = 0) P 0 0 p(b = 0) Q p(a = 1) 1 1 p(b = 1) C = max {I(A; B) : p(a)} = max {H(B) - W : p(a)} = max where x = p. P + (1 − p)Q p = p(a = 0) maximum occurs when x = ½, p = ½ also (unless all noise). C = 1 − H 2(P) 8. 5

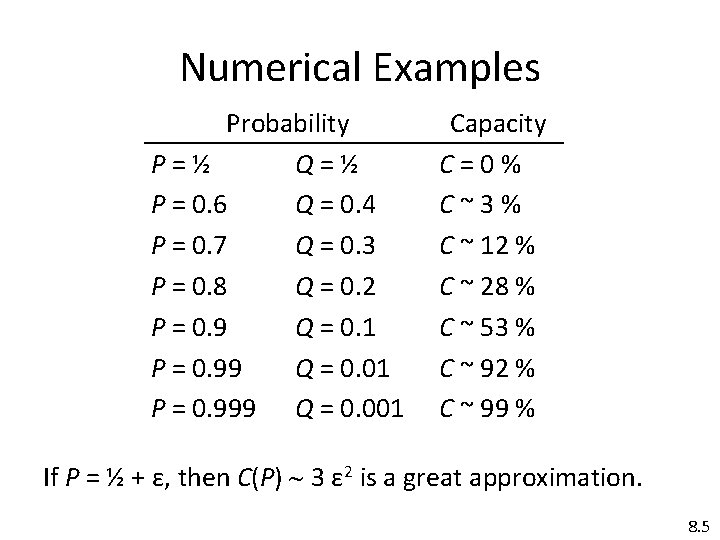
Numerical Examples Probability P = ½ Q = ½ P = 0. 6 Q = 0. 4 P = 0. 7 Q = 0. 3 P = 0. 8 Q = 0. 2 P = 0. 9 Q = 0. 1 P = 0. 99 Q = 0. 01 P = 0. 999 Q = 0. 001 Capacity C = 0 % C ~ 3 % C ~ 12 % C ~ 28 % C ~ 53 % C ~ 92 % C ~ 99 % If P = ½ + ε, then C(P) 3 ε 2 is a great approximation. 8. 5

Error Detecting Code A uniform channel with equiprobable input: p(a 1) = … = p(aq). Apply to n-bit single error detection, with one parity bit among ci {0, 1}: |A| = q = 2 n− 1 a = c 1 … cn (even parity) H 2(A) = n − 1 P Q Q P |B| = 2 n = 2 q c 1 … cn = b (any parity) H 2(B) = ? ? For blocks of size n, we know the probability of k errors = every b B can be obtained from any a A by k = 0 … n errors: 8. 3
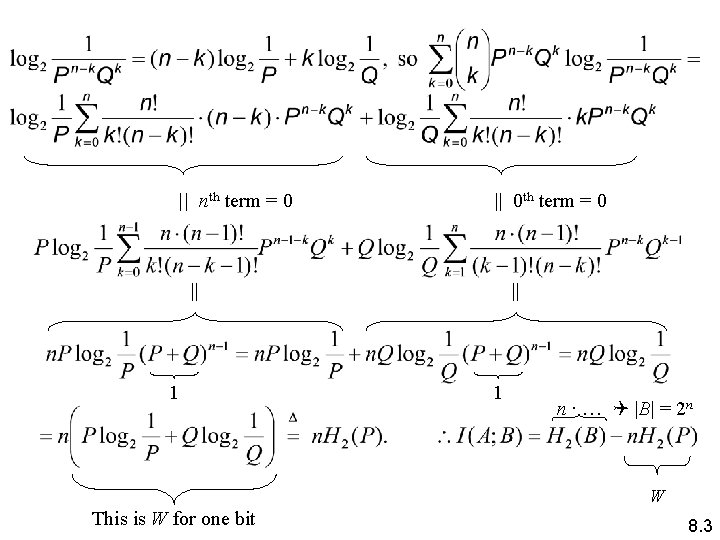
|| nth term = 0 || 0 th term = 0 || 1 n ∙ … |B| = 2 n W This is W for one bit 8. 3

Error Correcting Code encode P Q Q P decode × 3 noisy channel 3 triplicate majority think of this as the channel uncoded original prob. of no errors = P 3 prob. of 1 error = 3 P 2 Q prob. of 2 errors = 3 PQ 2 prob. of 3 errors = Q 3 vs. = new probability of no error probability = of an error P 3+3 P 2 Q 3 PQ 2+Q 3 P 3+3 P 2 Q let P′ = P 2·(P + 3 Q) 8. 4

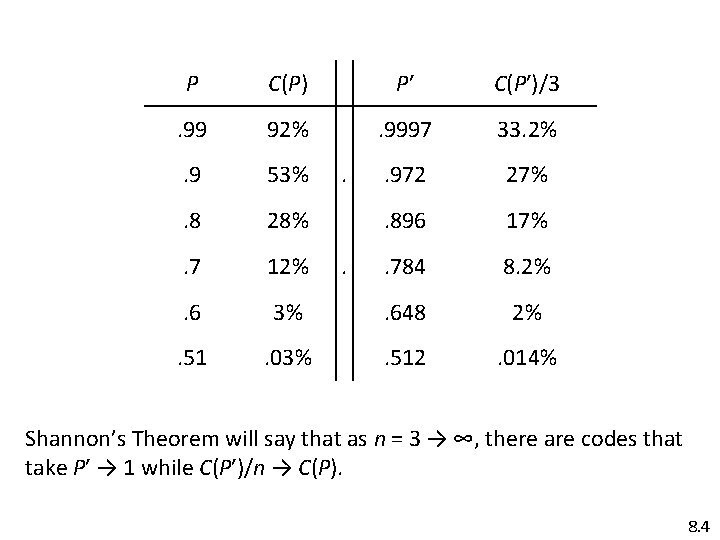
P C(P) P′ C(P′)/3 . 99 92% . 9997 33. 2% . 9 53% . 972 27% . 8 28% . 896 17% . 7 12% . 784 8. 2% . 6 3% . 648 2% . 51 . 03% . 512 . 014% . . Shannon’s Theorem will say that as n = 3 → ∞, there are codes that take P′ → 1 while C(P′)/n → C(P). 8. 4