Chapter 15 Concatenated codes Simple classical singlelevel concatenation

(Chapter 15): Concatenated codes • Simple (classical, single-level) concatenation • Length of concatenated code: n 1 n 2 • Dimension of concatenated code: k 1 k 2 • If minimum distances of component codes are d 1 and d 2 , respectively, then the concatenated code has minimum distance d 1 d 2 • Decoding: • Two-stage: Decode (Hard decision out) inner code, then outer code • Not optimum! Can decode up to approximately ¼ of min. dist. 1 • Good for decoding mixture of random and burst errors

Multiple Inner Codes • Not necessary that all inner codes are identical • Justesen codes: • n 2 different inner codes • Can show that a good class of codes can be constructed this way • A class {Ci} of codes of increasing lengths ni is good if the normalized dimensions ki/ni and the normalized minimum distances di/ni are both bounded away from zero. • A theoretical result; first known class of good codes 2

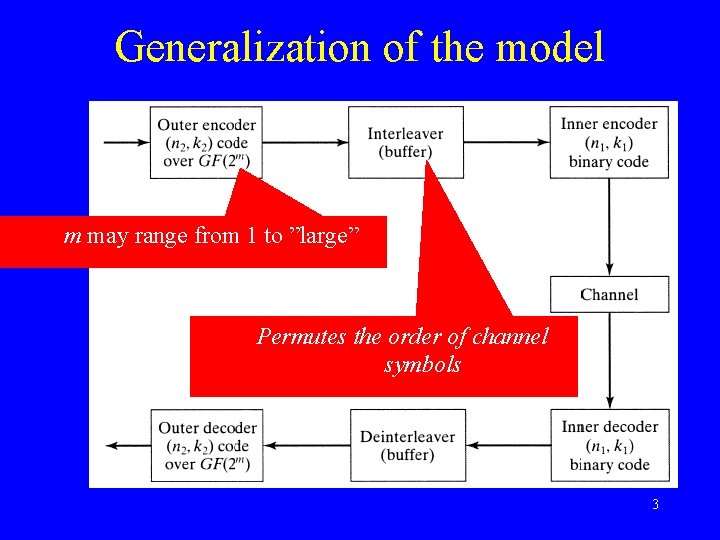
Generalization of the model m may range from 1 to ”large” Permutes the order of channel symbols 3

Example of interleaved serial concatenation 4

Multilevel concatenated codes • Multiple outer and inner codes K 1 N K 2 N Km N A 1 A 2. . . Am {0} ki dimension of Ai d(Ai) min. dist. of Ai [Ai/Ai+1] coset code: set of coset representatives; dimension ki - ki+1 • qi = 2 ki-ki+1 • Bi code over GF(qi) • • • K = Ki(ki - ki+1) • d(C) min{d(Bi)d(Ai)} 5

Multi-stage decoding • • m-level multilevel concatenation: Decode stage B 1 [A 1/A 2] first, . . . , stage Bm Am last 1. Decode r = r(1) into a codeword b 1 in B 1 Inner decoding: Find closest word in [A 1/A 2] Outer decoding: Use inner decoder’s results Set i=2; 2. Let r(i) = r(i-1) – fi-1(bi-1). Decode r(i) into a codeword bi in Bi Set i=i+1; If (i m), repeat from 2. 6

Soft decision multistage decoding • • Requires soft decision (and usually trellis based) decoding at each decoding stage Decode stage B 1 [A 1/A 2] first, . . . , stage Bm Am last 1. Decode r = r(1) into a codeword b 1 in B 1 Inner decoding: Find closest word in [A 1/A 2] Outer decoding: Use inner decoder’s results Set i=2; 2. Modify received vector r(i) : rj, l(i) = rj, l(i-1) (1 -2 cj, l(i-1)) Decode r(i) into a codeword bi in Bi Set i=i+1; If (i m), repeat from 2. 7

Inner and outer decoding • • • Inner decoder: • Find the word (label) in each coset in [Ai/Ai+1] with largest metric for each symbol of the outer code • Pass these metric tables to the outer decoder Outer decoder: • Find word with largest metric Not MLD because of possible error propagation Simpler than known MLD algorithms for such codes Can be improved by passing a list of L candidates from one decoding stage to the next; and by selecting as the final decoded word the one wth the largest metric at the final stage 8

Code decomposition • Expressing a code in terms of a multilevel concatenation • -level decomposable code: can be expressed as a -level concatenated code • Some classical code constructions may be expressed in this way. This may facilitate decoding of such codes, and can provide SD decoding • r-th order Reed-Muller code of length 2 m, RM(r, m) • Idea: Decompose trellis into trellises, each trellis significantly less complex than the original 9

Properties of RM(r, m) • v 0=(1. . . 1) of length 2 m • vi=(0. . . 0, 1. . . 1, 0. . . 0, . . . . , 1. . . 1) (groups of length 2 i-1) • RM(r, m) is spanned by vectors: v 0, v 1, v 2 , . . . , vm, v 1 v 2 , v 1 v 3 , . . . , vm-1 vm, . . . all products of degree up to r • k(r, m) = 1+C(m, 1)+. . . +C(m, r), q(r, m) = C(m, r) • Minimum distance 2 m-r • RM(r, m) RM(r-1, m) . . . RM(0, m) = {0, 1} RM(-1, m) = {0} • RM(m-1, m) is a single parity check code • RM(m-r-1, m) is the dual code of RM(r, m) 10

RM codes and interleaving • RM(r, m) = {RM(0, )q(r, m- ), RM(1, )q(r-1, m- ), . . . , RM( , )q(r- , m- )} {RM(r, m- ), RM(r-1, m- ), . . . , RM(r- , m- )}. . . for any , : 1 m-1, = for r> , =r for r . • Example: RM(3, 6) , a (64, 42, 8) code. Select = =3 • RM(3, 6) = {RM(0, 3)q(3, 3), RM(1, 3)q(2, 3), RM(2, 3)q(1, 3), RM(3, 3)q(0, 3)} {RM(3, 3), RM(2, 3), RM(1, 3), RM(0, 3)} • = {(8, 1), (8, 4)3, (8, 7)3, (8, 8)} {(8, 8), (8, 7), (8, 4), (8, 1)} = (8, 1) [(8, 8)/(8, 7)] (8, 4)3 [(8, 7)/(8, 4)] (8, 7)3 [(8, 4)/(8, 1)] (8, 8) [(8, 1)/{0}] 12

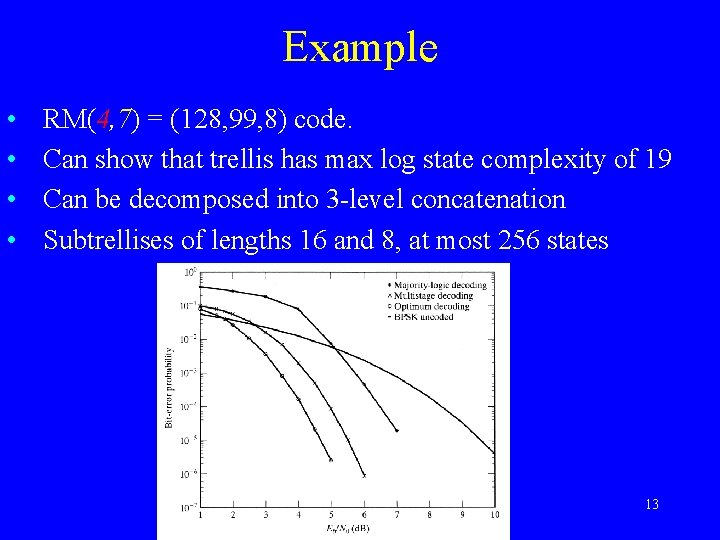
Example • • RM(4, 7) = (128, 99, 8) code. Can show that trellis has max log state complexity of 19 Can be decomposed into 3 -level concatenation Subtrellises of lengths 16 and 8, at most 256 states 13

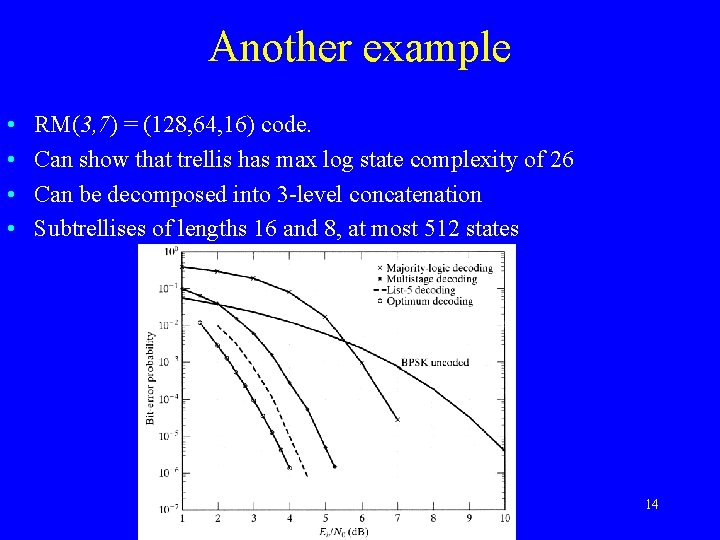
Another example • • RM(3, 7) = (128, 64, 16) code. Can show that trellis has max log state complexity of 26 Can be decomposed into 3 -level concatenation Subtrellises of lengths 16 and 8, at most 512 states 14

Iterative multistage MLD algorithm • Decoding algorithm (m=2 -stage decoding) 1. Compute best estimate b(1), 1 of first decoding stage, and M(b(1), 1). If coset label sequence L(b(1), 1) C: Best codeword found, so stop, otherwise proceed to 2. 2. Second stage decoding, obtain L(b(2), 1), M(b(2), 1). Store b(1), 1 and b(2), 1. Set i 0=1, i=2. 3. Calculate b(1), i and b(2), i. If M(b(2 ), i 0)> M(b(1), i), decoding is finished, and b(1), i 0 and b(2), i 0 give the most likely codeword. Otherwise go to 4. 4. If coset label L(b(1), i) C: Best codeword found, so stop, otherwise proceed to 5. 5. If M(b(2 ), i)> M(b(2), i 0), set i 0=i and update tables and index i. Go to 3. 15

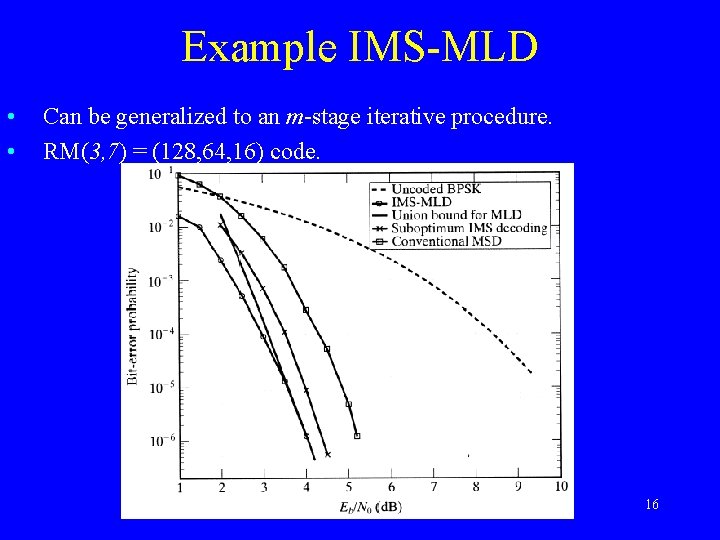
Example IMS-MLD • • Can be generalized to an m-stage iterative procedure. RM(3, 7) = (128, 64, 16) code. 16

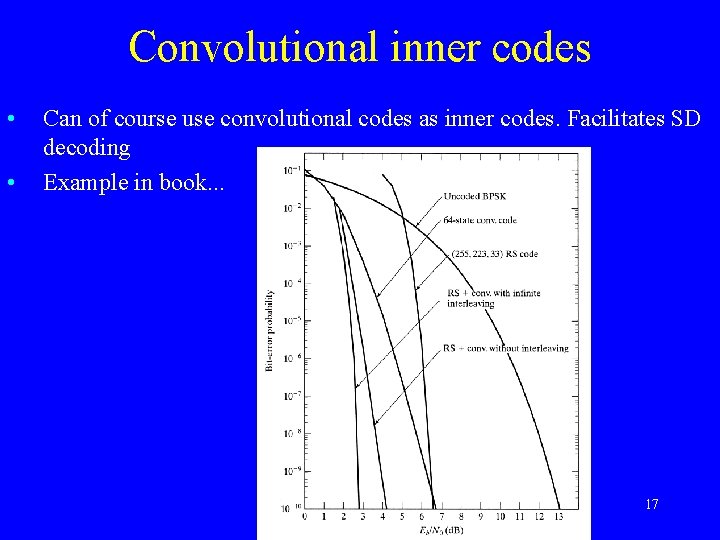
Convolutional inner codes • • Can of course use convolutional codes as inner codes. Facilitates SD decoding Example in book. . . 17

Concatenation of binary codes • Also possible with binary outer codes (block or convolutional) • More difficult to make statements about overall minimum distance • Interleaver useful for increasing distance • SISO algorithms useful • Iterative decoding useful • Serial concatenation/Parallel concatenation 18

Suggested exercises • In principle: All Ch. 15 problems • But some rely on insight in the RM codes 19