Changing Magnetic Flux Faradays Law Mathematically we can

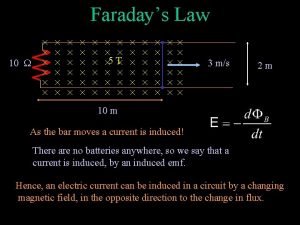
Changing Magnetic Flux: Faraday’s Law Mathematically, we can express the motion-induced voltage in any closed path as the rate of change (over time) of the area of that loop times the perpendicular B-field passing through that area. That is (in non-differential form): | V| = [(B·cos )A]/ t M is called the magnetic flux of the loop: M = B • A = (B·cos )A where is the angle between B and the normal to the loop of area A. The SI unit of magnetic flux is the Weber (Wb). 1 Wb = 1 T·m 2 Written as an instantaneous value, we then have: | V(t)| = d/dt[ M] 5/24/19 Oregon State University PH 213, Class #24 1

What Can Change the Magnetic Flux? The changing nature of a loop (area or angle) in a magnetic field is not the only way to change the flux = (B·cos )A. There’s a third variable: Even if the loop remains motionless and unchanging, the flux can change if the magnitude or direction of the magnetic field, B, is changing. Faraday’s Law states that any of these will cause an induced voltage in a closed loop whose area is intersected by a magnetic field, B: ･ Change the area of the loop; ･ Change the orientation of the loop; ･ Change the magnitude of B; ･ Change the direction of B. 5/24/19 Oregon State University PH 213, Class #24 2

Try the “averaging” version of Faraday’s Law: | Vavg| = / t Suppose that at a certain location the earth’s natural magnetic field is 5 x 10 -5 T, directed into the ground at an angle of 40° below the horizontal. A circular ring of copper (2 m in diameter) is initially lying flat on the ground, but then is tilted until its normal is aligned with the B-field. If this takes 0. 5 sec, and if the ring of copper has 0. 2 of resistance, what average current flows around the ring? 5/24/19 A. 5. 61 x 10 -5 A B. 1. 12 x 10 -4 A C. 3. 67 x 10 -4 A D. 5. 61 x 10 -4 A E. None of the above. Oregon State University PH 213, Class #24 3

Now repeat the previous example and derive I(t), a time function for the current flowing in the ring, using the instantaneous version of Faraday’s Law: | V(t)| = d/dt[ M] (Assume that your tilting of the ring is done at a steady angular rate, w. ) Could you then go on to calculate the energy produced by the resistance in the copper? It would be equal to the work needed to tilt the ring (and this is not about lifting the ring against gravity). 5/24/19 Oregon State University PH 213, Class #24 4

Where is the Induced E-Field Directed? | V(t)| = d/dt[ M] Faraday’s Law is only about the magnitude of V. The direction of the E-field producing the V is given by Lenz’s Law: The E-field induced by a change in flux is directed so that its resulting current (if allowed to flow) would cause a magnetic field that opposes that change in flux. Example: Move a bar magnet toward a loop. Note: Lenz’s law is basically just a restatement of the conservation of energy. If the above “oppositional” orientation were not the case, any increase in flux would induce a current that would further increase that flux, which would induce more current, etc. —a perpetual motion machine driven by an ever-increasing supply of suddenly-appearing energy. (Not gonna happen. ) 5/24/19 Oregon State University PH 213, Class #24 5

A conductive loop is placed flat upon an insulated surface. A bar magnet is initially standing on end, on its north pole, at the center of this loop. It is then lifted vertically, directly away up from the loop. As viewed from above, which way will current flow in the loop? A. Clockwise. B. Counter-clockwise. C. It depends how fast the magnet is lifted. D. It depends on the area of the loop. E. No current will flow. 5/24/19 Oregon State University PH 213, Class #24 6

The magnet is falling downward away from the stationary loop. What is the direction of the induced current (if any) in the loop, as viewed from above? 1. 2. 3. 5/24/19 No induced current Clockwise induced current Counterclockwise induced current Oregon State University PH 213, Class #24 7

A current-carrying wire is pulled away from a conducting loop in the direction shown. As the wire is moving, what (if any) current appears in the loop? 1. 2. 3. 5/24/19 There is no current around the loop. There is a clockwise current around the loop. There is a counterclockwise current around the loop. Oregon State University PH 213, Class #24 8

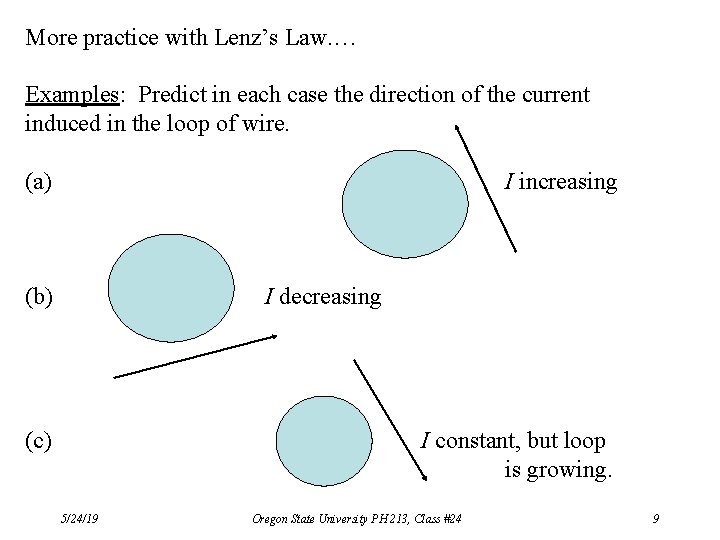
More practice with Lenz’s Law. … Examples: Predict in each case the direction of the current induced in the loop of wire. (a) I increasing (b) I decreasing (c) I constant, but loop is growing. 5/24/19 Oregon State University PH 213, Class #24 9

More practice with Lenz’s Law. … Examples: With a magnetic field, B, directed into the page (X), predict the direction of the current induced in a simple wire loop for each case of flux change. (a) B increasing (b) B decreasing (c) B constant but loop growing 5/24/19 Oregon State University PH 213, Class #24 10

A rectangular loop of wire was falling freely before it passes through a uniform magnetic field directed into the page. With the loop in the position shown… What is the direction of the induced current, I, in the loop? And what is the direction of the net magnetic force, Fmag, on the loop? A. I is clockwise; Fmag is upward. B. I is counter-clockwise; Fmag is upward. C. I is clockwise; Fmag is downward. D. I is counter-clockwise; Fmag is downward. E. None of the above. 5/24/19 Oregon State University PH 213, Class #24 11

Applications of Induction: Magnetic Braking (using eddy currents) 5/24/19 Oregon State University PH 213, Class #24 12