CE 40763 Digital Signal Processing Fall 1992 Discretetime

CE 40763 Digital Signal Processing Fall 1992 Discrete-time Fourier Transform Hossein Sameti Department of Computer Engineering Sharif University of Technology

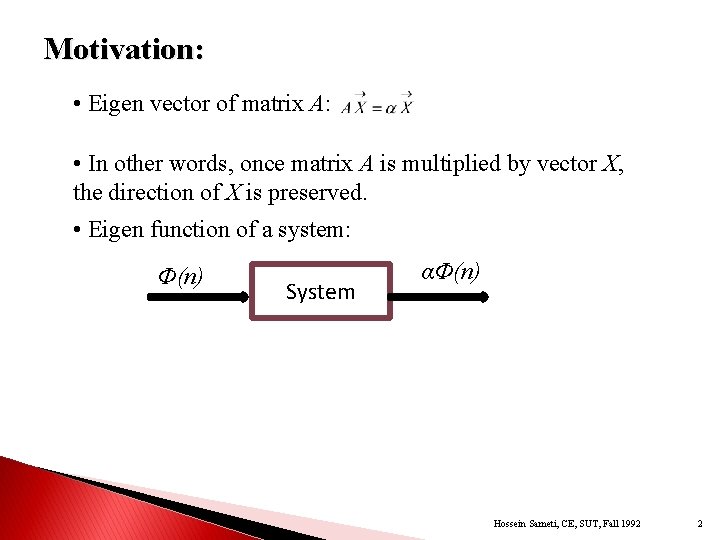
Motivation: • Eigen vector of matrix A: • In other words, once matrix A is multiplied by vector X, the direction of X is preserved. • Eigen function of a system: Ф(n) System αФ(n) Hossein Sameti, CE, SUT, Fall 1992 2

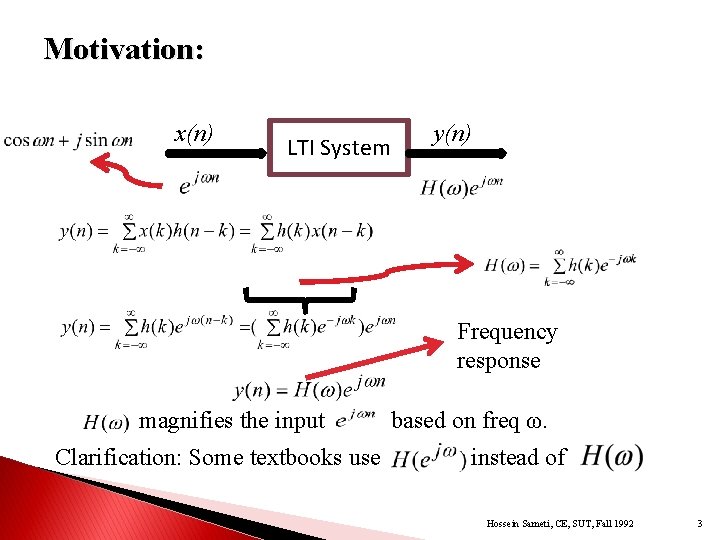
Motivation: x(n) LTI System y(n) Frequency response magnifies the input Clarification: Some textbooks use based on freq ω. instead of Hossein Sameti, CE, SUT, Fall 1992 . 3

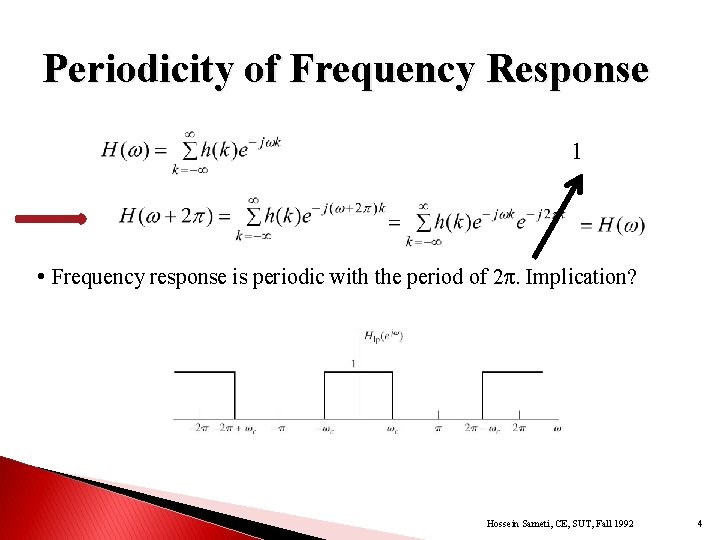
Periodicity of Frequency Response 1 • Frequency response is periodic with the period of 2π. Implication? Hossein Sameti, CE, SUT, Fall 1992 4

Low/high Frequencies in Discrete-time domain Hossein Sameti, CE, SUT, Fall 1992 5

Convergence of the Frequency Response The same condition as the stability condition Hossein Sameti, CE, SUT, Fall 1992 6

Discrete-Time Fourier Transform Same mathematical representation as the freq. response • Existence of DTFT: x(n) is absolutely summable. • Inverse DTFT: u u Fourier analysis considers signals to be constructed from a sum of complex exponentials with appropriate frequencies, amplitudes and phase. Frequency components are the complex exponentials which, when added together, make up the signal. Hossein Sameti, CE, SUT, Fall 1992 7

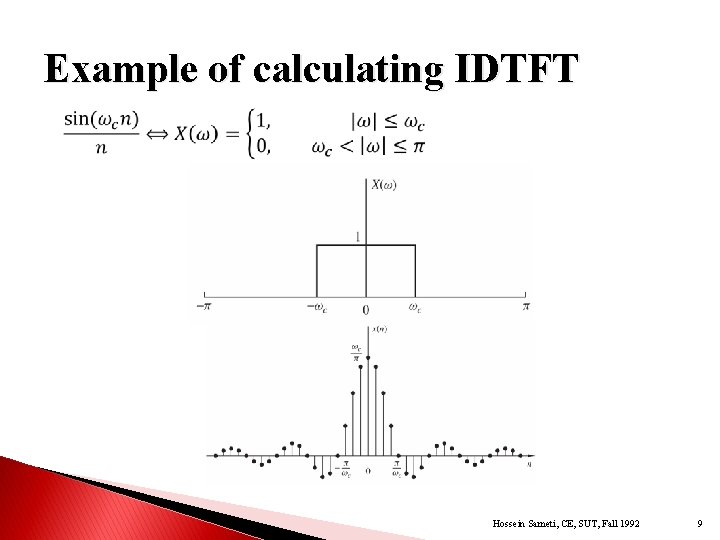
Example of calculating IDTFT of the ideal low-pass filter: Hossein Sameti, CE, SUT, Fall 1992 8

Example of calculating IDTFT Hossein Sameti, CE, SUT, Fall 1992 9

Real and Imaginary parts of DTFT? What happens if a>1? Hossein Sameti, CE, SUT, Fall 1992 10

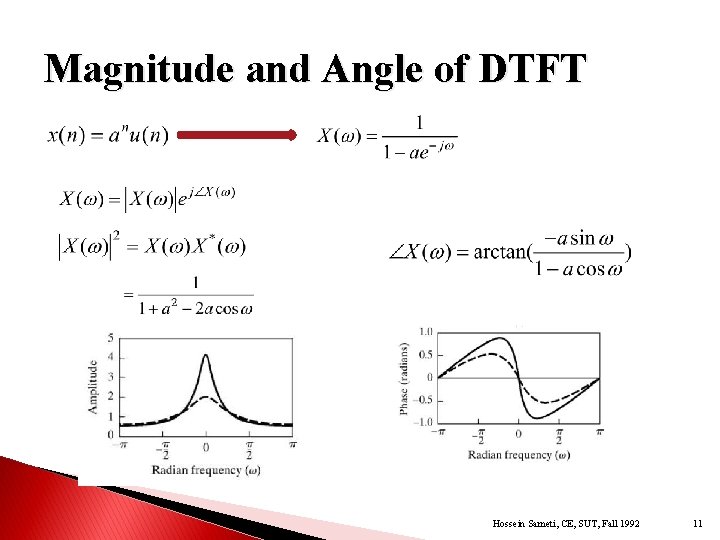
Magnitude and Angle of DTFT Hossein Sameti, CE, SUT, Fall 1992 11

DTFT Pairs Hossein Sameti, CE, SUT, Fall 1992 12

DTFT Pairs Hossein Sameti, CE, SUT, Fall 1992 13

Properties of DTFT • Linearity: • Time-shifting: • Time-reversal: • Convolution : x(n) LTI System h(n) y(n) Hossein Sameti, CE, SUT, Fall 1992 14

Properties of DTFT • Cross-correlation: • Frequency Shifting: • Parseval’s Theorem: Hossein Sameti, CE, SUT, Fall 1992 15

Properties of DTFT • Modulation: • Multiplication: • Differentiation in the freq. domain: • Conjugation: Hossein Sameti, CE, SUT, Fall 1992 16

Symmetry Properties of DTFT • Conjugate Symmetric: • Conjugate Anti-Symmetric: • Why are these properties important? Conjugate Symmetric Conjugate Anti-symmetric Hossein Sameti, CE, SUT, Fall 1992 17

Symmetry Properties of DTFT Hossein Sameti, CE, SUT, Fall 1992 18

Symmetry Properties of DTFT : real • If a sequence is real, then its DTFT is conjugate symmetric. Hossein Sameti, CE, SUT, Fall 1992 19

Symmetry Properties of DTFT : real : real Hossein Sameti, CE, SUT, Fall 1992 20

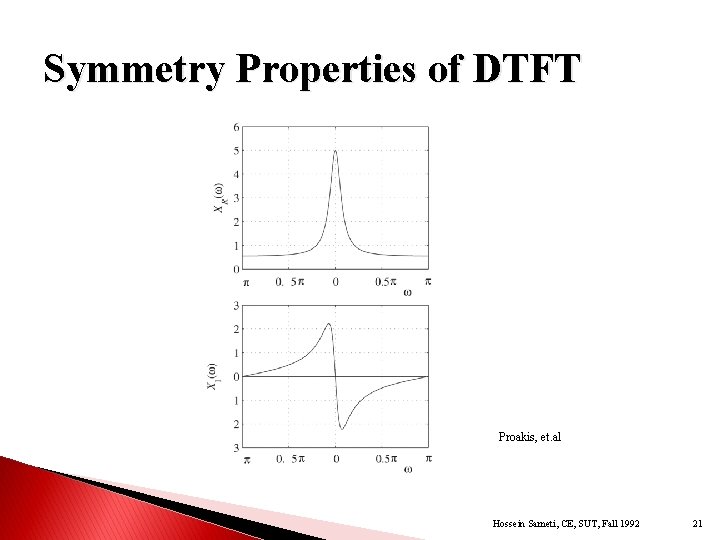
Symmetry Properties of DTFT Proakis, et. al Hossein Sameti, CE, SUT, Fall 1992 21

Example: Determining an inverse fourier transform Hossein Sameti, CE, SUT, Fall 1992 22

Example: Determining the Impulse response from the frequency response Hossein Sameti, CE, SUT, Fall 1992 23

Example: Determining the Impulse response for a Difference Equation To find the impulse response h[n], we set Applying the DTFT to both sides of equation. We obtain Hossein Sameti, CE, SUT, Fall 1992 24

Example: Hossein Sameti, CE, SUT, Fall 1992 25

Summary Reviewed Discrete-time Fourier Transform, some of its properties and FT pairs Next: the Z-transform Hossein Sameti, CE, SUT, Fall 1992 26