BAB VI Metode Root Locus Pengertian Root locus

BAB VI Metode Root Locus
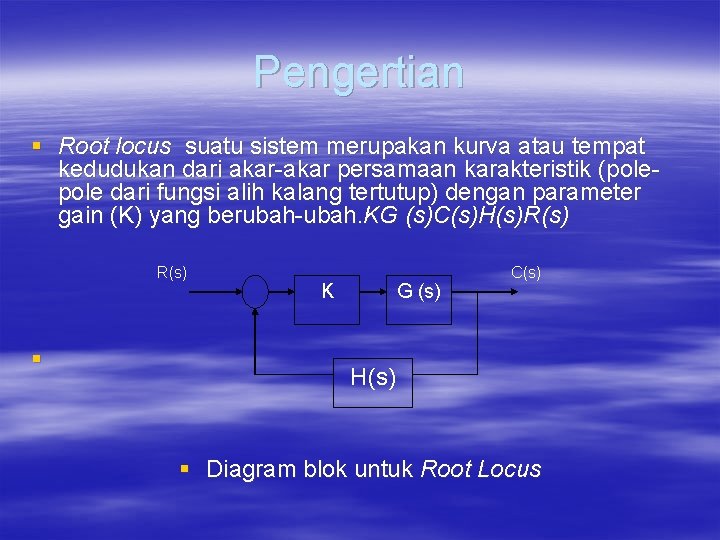
Pengertian § Root locus suatu sistem merupakan kurva atau tempat kedudukan dari akar-akar persamaan karakteristik (pole dari fungsi alih kalang tertutup) dengan parameter gain (K) yang berubah-ubah. KG (s)C(s)H(s)R(s) § K G (s) C(s) H(s) § Diagram blok untuk Root Locus

Lanjutan § Persamaan karakteristik sistem: § Nilai s berada pada Root Locus jika s memenuhi persamaan di atas. Karena s dapat merupakan bilangan kompleks, maka dari persamaan tersebut, s adalah sebuah titik pada Root Locus jika memenuhi syarat magnitude: § Dengan syarat sudut:

Aturan-aturan menggambarkan Root Locus § Root Locus mempunyai sifat simetri terhadap sumbu nyata. § Menentukan pole-pole dan zero-zerodari fungsi alih kalang terbuka sistem KG(s)H(s). Root Locus bermula dari pole-pole (untuk K=0) dan berakhir zero-zero (untuk K ∞) termasuk zero-zero pada titik tak hingga. § Menentukan asimptot θ dan titik potongnya dengan sumbu nyata σ dapat dihitung dengan rumus: §

lanjutan § dengan r = ± 1, ± 3, ± 5, . . . dan α = banyaknya zero pada titik tak hingga dan § Menentukan daerah cakupan Root Locus pada sumbu nyata: – Root Locus mencakup titik-titik pada sumbu nyata di sebelah kiri frekuensi kritis (pole-pole dan zero-zero) nyata yang berjumlah ganjil.

lanjutan § Menentukan titik pencar (titik pisah atau titik temu), yang terdapat di antara akar-akar § dengan N(s) dan D(s) masing-masing merupakan numerator dan denumerator G(s)H(s).
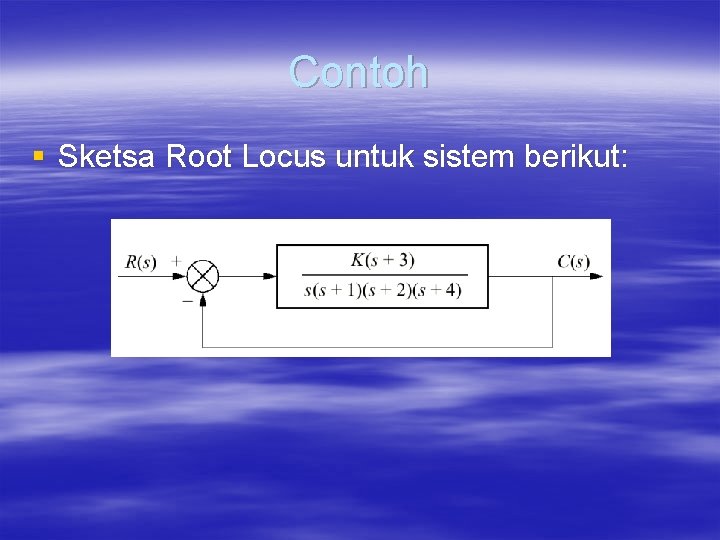
Contoh § Sketsa Root Locus untuk sistem berikut:

Jawaban

Root Locus menggunakan Matlab § Contoh sistem: § Cara menggunakan Matlab
- Slides: 9