Asymptotic Notations Algorithms Lecture 9 Growth of functions

Asymptotic Notations Algorithms Lecture 9

Growth of functions • The order of growth of the running time of an algorithm, gives a simple characterization of the algorithm’s efficiency and also allow us to compare the relative performance of alternative algorithms. • Once the input size n becomes large enough , Merge sort ( in the worst case ) with its ( n log n ) out performs Insertion sort in the worst case whose running time is (n 2 ). • We are studying the asymptotic efficiency of algorithms. That is , we are concerned with how the running time of an algorithm increases with the size of the input in the limit, as the size of the input increased without bound. • So, we give a bound to the running time when the input increased without bound. 2 Algorithms Lecture 9 Dr. Arwa Zabian

Asymptotic Notations • The notation we use to describe the asymptotic running time of an algorithm are defined in terms of functions. Whose domain are the set of natural numbers N={0, 1, 2, 3…}. • So, using the asymptotic notation we describe the running time T(n) of an algorithm for an integer input size 3 Algorithms Lecture 9 Dr. Arwa Zabian

Notation • Definition : for a given function g(n) , we denote (g(n)) the set of functions (g(n)) = { f(n): there exists a positive constant c 1 , c 2 and n 0 , such that : 0 c 1 g(n) f(n) c 2 g(n) for all n n 0 } That means we must choose a value n 0 from which the definition of is hold If the definition of is hold for n n 0. means give upper bound and lower bound. That means give an equal bound. 4 Algorithms Lecture 9 Dr. Arwa Zabian

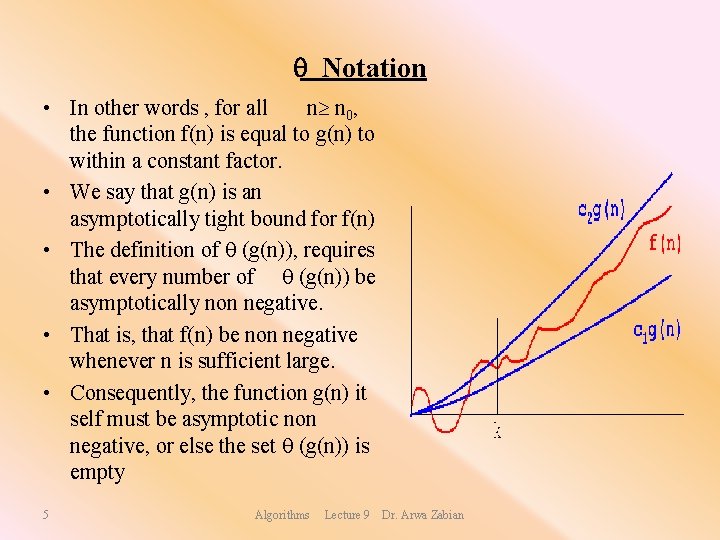
Notation • In other words , for all n n 0, the function f(n) is equal to g(n) to within a constant factor. • We say that g(n) is an asymptotically tight bound for f(n) • The definition of (g(n)), requires that every number of (g(n)) be asymptotically non negative. • That is, that f(n) be non negative whenever n is sufficient large. • Consequently, the function g(n) it self must be asymptotic non negative, or else the set (g(n)) is empty 5 Algorithms Lecture 9 Dr. Arwa Zabian

Exercise • Use the formal description to show that g(n) = ½ n 2 - 3 n = (n 2 ) solution : To do so, we must determine positive constant c 1 , c 2 and n 0 such that: c 1 n 2 ½ n 2 – 3 n c 2 n 2 for all n n 0 dividing by n 2 yields: 6 Algorithms Lecture 9 c 1 ½ - 3/n c 2 For 7 > n 1 G(n) always negative so, we choose n 0 = 1/14 and c 1 = 1/14 , c 2 =1/2 That means for all n 0 7 we can find two constant that makes the inequality correct. That means g(n)= (n 2 ) Dr. Arwa Zabian

Exercise • Using the formal definition proof that 6 n 3 ≠ (n 2 ) We assume that 6 n 3 = (n 2 ) So given the definition for all n n 0 C 1 n 2 6 n 3 c 2 n 2 c 1 6 n c 2 /6 Which cannot possibly hold for arbitrary large n , since c 2 is constant 7 Algorithms Lecture 9 Dr. Arwa Zabian

O -notation • O notation gives an asymptotic upper bound • Definition : for a given function g(n) , we denote O (g(n)) the set of functions O(g(n)) = { f(n): there exists a positive constant c, and n 0 , such that : 0 f(n) c g(n) for all n n 0 } • For all value n to the right of n 0 , the value of the function f(n) is on or below g(n). • O notation gives an upper bound on a function • Using O-notation , we can often describe the running time of an algorithm merely by inspection the algorithm’s over all structure. 8 Algorithms Lecture 9 Dr. Arwa Zabian

Exercise • The algorithm is composed on two loops. The inner loop while for j 2 to length[A] is executed one time its cost O(1) that consists on assignment do key A[j] to the key and comparisons. insert A[j] into the sorted • The indices i, j are executed n sequence A[1…. j-1] times i j-1 • So immediately we say that the running time is O(n 2) in the While i> 0 and A[i] < key worst case. Insertion sort 1. 2. 3. 4. 5. 6. do A[i+1] 7. i i-1 8. A[i+1] 9 A[i] key Algorithms Lecture 9 Dr. Arwa Zabian

O -notation • When we said the running time is O (n 2) in the worst case means : 1. the algorithm cannot run worst than n 2 2. This value is for every input • however, (n 2) in the worst case does not imply a bound on the running time for every input ( but specific input ) That means O is more general than So, we are interested in studying the behavior of the algorithm when the input is increased. 10 Algorithms Lecture 9 Dr. Arwa Zabian

notation • notation provides an asymptotic lower bound • Definition : for a given function g(n) , we denote (g(n)) the set of functions (g(n)) = { f(n): there exists a positive constant c, and n 0 , such that : 0 c g(n) f(n) for all n n 0 } • For all value n to the right of n 0 , the value of the function f(n) is on or above g(n). 11 Algorithms Lecture 9 Dr. Arwa Zabian

Theorem • For any two functions f(n) and g(n), f(n) = (g(n)) if and only if : f(n) = O(g(n)) and f(n) = (g(n)) That means has the same asymptotic bound if and only if is upper and lower bounded by g 12 Algorithms Lecture 9 Dr. Arwa Zabian