Advanced Digital Signal Processing Prof Nizamettin AYDIN naydinyildiz

Advanced Digital Signal Processing Prof. Nizamettin AYDIN naydin@yildiz. edu. tr http: //www. yildiz. edu. tr/~naydin 1

• Time-Scale Analysis – Wavelet Transform – Complex Wavelet 2

Introduction • Stroke is an illness causing partial or total paralysis, or death. • The most common type of stroke (80% of all strokes) occurs when a blood vessel in or around the brain becomes plugged. • The plug can originate in an artery of the brain or somewhere else in the body, often the heart, where it breaks off and travels up the arterial tree to the brain, until it lodges in a blood vessel. 3

Emboli • These "travelling clots" are called emboli. • Solid emboli typically consist of – thrombus, – hard calcified plaque or – soft fatty atheroma. • Gaseous emboli may also enter the circulation during surgery or form internally from gases that are normally dissolved in the blood. • Any foreign body (solid or gas) that becomes freefloating in the bloodstream is called an embolus, from the Greek ‘embolos’ meaning ‘a stopper’. 4

• Early and accurate detection of asymptomatic emboli is important in identifying patients at high risk of stroke • They can be detected by Doppler ultrasound – Transcranial Doppler ultrasound (TCD) • 1 -2 MHz 5

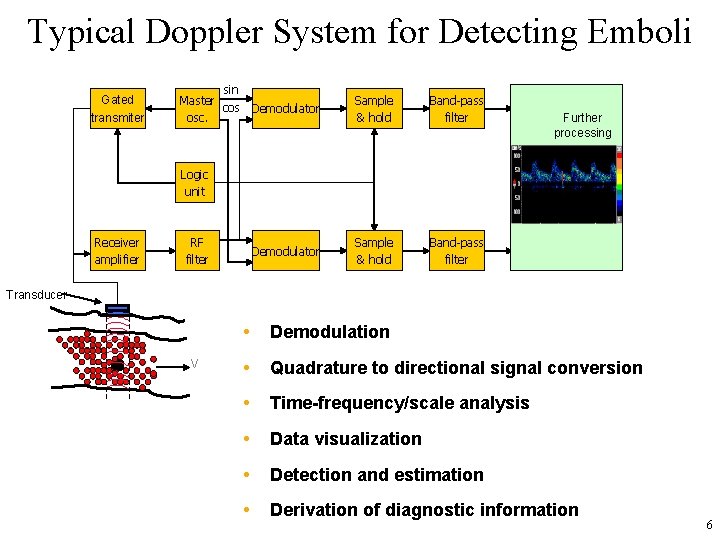
Typical Doppler System for Detecting Emboli Gated transmiter sin Master cos Demodulator osc. Sample & hold Band-pass filter si Further processing Logic unit Receiver amplifier RF filter Demodulator Transducer V • Demodulation • Quadrature to directional signal conversion • Time-frequency/scale analysis • Data visualization • Detection and estimation • Derivation of diagnostic information 6

Embolic Doppler ultrasound signal • Within audio range (0 -10 k. Hz) • Appear as increasing and then decreasing in intensity for a short duration, – usually less than 300 ms. • The bandwidth of ES is usually much less than that of Doppler Speckle. – narrow-band signals • They are also oscillating and finite signals – Similar to wavelets. • Have an associated characteristic click or chirping sound • Unidirectional and usually contained within the flow spectrum • The spectral content of an ES is also time dependent. 7

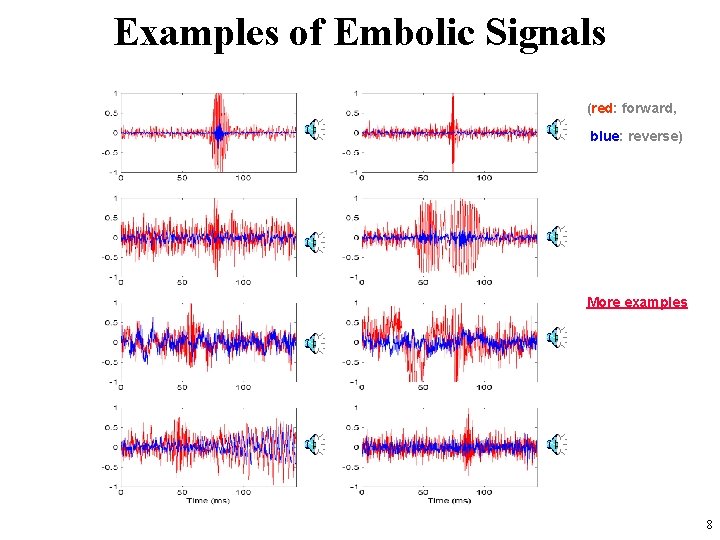
Examples of Embolic Signals (red: forward, blue: reverse) More examples 8

9

Time-Scale Analysis (Continuous Wavelet Transform) • *(t) is the analysing wavelet. a (>0) controls the scale of the wavelet. b is the translation and controls the position of the wavelet. • Can be computed directly by convolving the signal with a scaled and dilated version of the wavelet (Frequency domain implementation may increase computational efficiency). • Wavelets are ideally suited for the analysis of sudden short duration signal changes (non-stationary signals). • Decomposes a time series into time-scale space, creating a three dimensional representation (time, wavelet scale and amplitude of the WT coefficients). 10

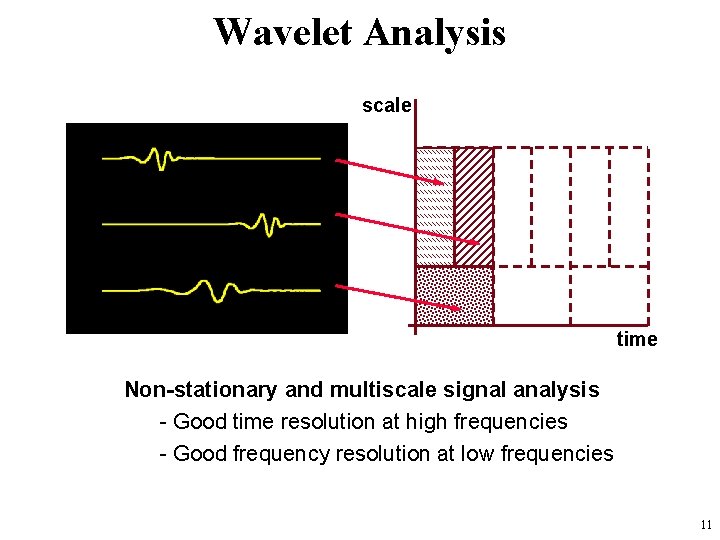
Wavelet Analysis scale time Non-stationary and multiscale signal analysis - Good time resolution at high frequencies - Good frequency resolution at low frequencies 11

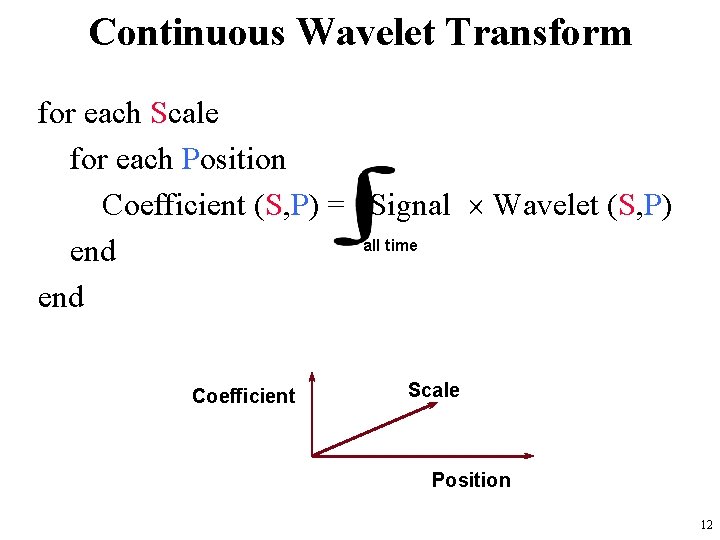
Continuous Wavelet Transform for each Scale for each Position Coefficient (S, P) = Signal Wavelet (S, P) all time end Coefficient Scale Position 12

Wavelet analysis and synthesis • A wavelet must oscillate and decay • a (>0) controls the scale of the wavelet. b is the translation parameter and controls the position of the wavelet. 13

Time-frequency and Time-scale analysis TF tiling is fixed. Assumes the signal is stationary within the analysis window. The FT has an inherent TF resolution limitation. TS tiling is logarithmic. Ideally suited for the analysis of sudden short duration signal changes. Allows TF resolution compromise to be optimised. 14

Time-Frequency Discretization Fourier frequency Shannon WFT time Wavelet 15

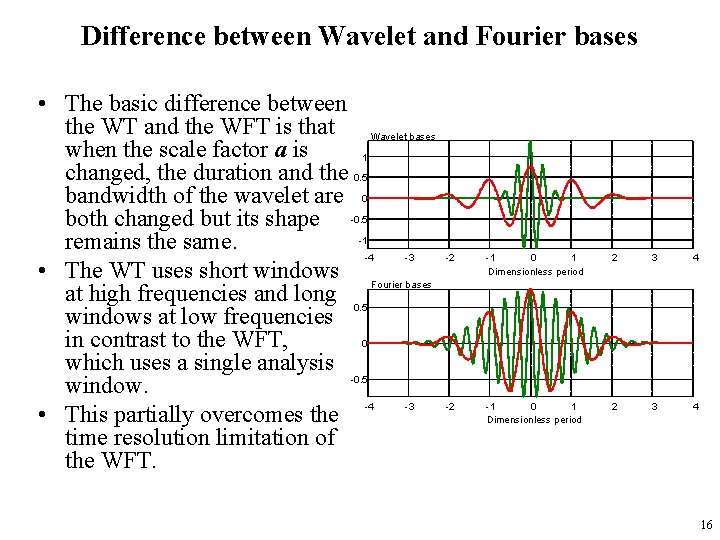
Difference between Wavelet and Fourier bases • The basic difference between the WT and the WFT is that Wavelet bases when the scale factor a is 1 changed, the duration and the 0. 5 bandwidth of the wavelet are 0 both changed but its shape -0. 5 -1 remains the same. -4 -3 • The WT uses short windows Fourier bases at high frequencies and long 0. 5 windows at low frequencies in contrast to the WFT, 0 which uses a single analysis -0. 5 window. • This partially overcomes the -4 -3 time resolution limitation of the WFT. -2 -1 0 1 Dimensionless period 2 3 4 16

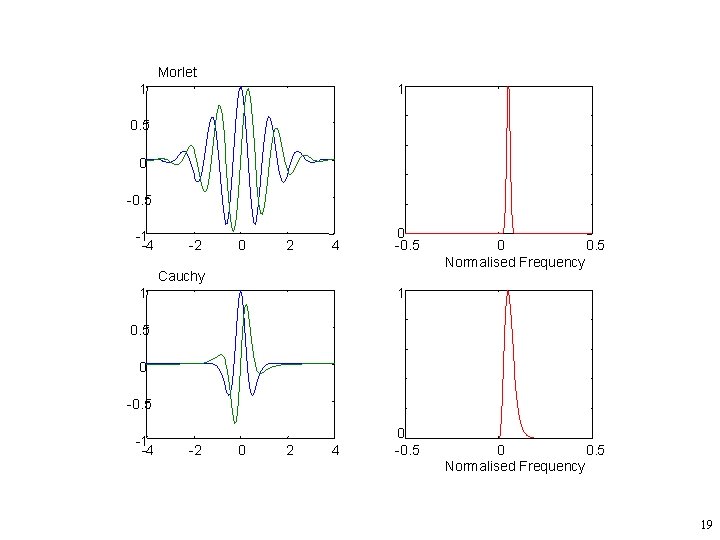
Complex Wavelet Transform • Similar to complex FT, a complex WT providing directional information in scale domain exists. • A complex wavelet (t) must also satisfy the following property: • Morlet and Cauchy wavelets are two examples for such complex wavelets. 17

• Complex Morlet wavelet. • Complex Cauchy wavelet. 18

Morlet 1 1 0. 5 0 -0. 5 -1 -4 -2 0 2 4 0 -0. 5 Cauchy 1 0 0. 5 Normalised Frequency 1 0. 5 0 -0. 5 -1 -4 -2 0 2 4 0 -0. 5 0 0. 5 Normalised Frequency 19

1 a<0 a>0 0. 5 -0. 5 0 Normalised Frequency 0. 5 20

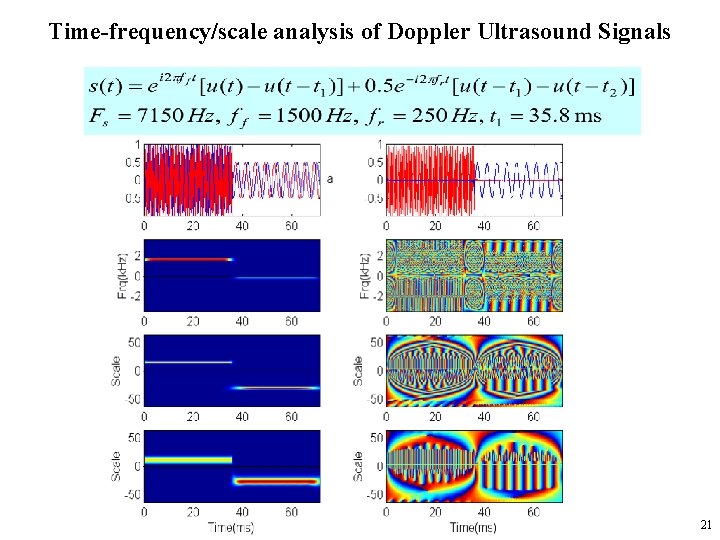
Time-frequency/scale analysis of Doppler Ultrasound Signals 21

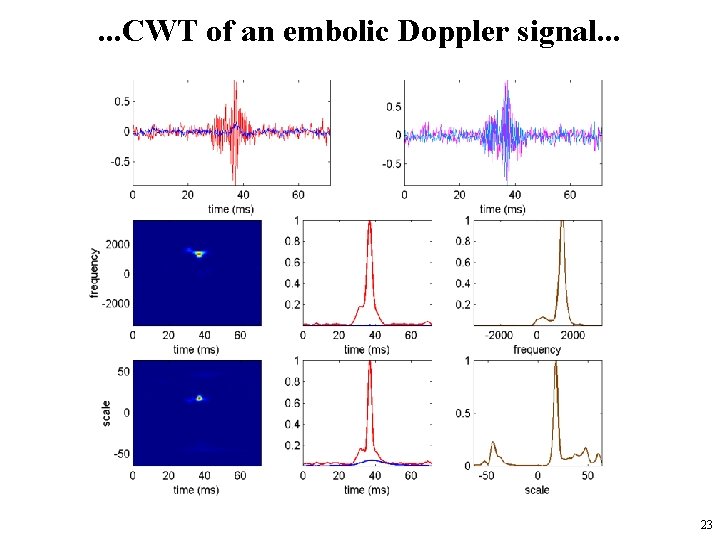
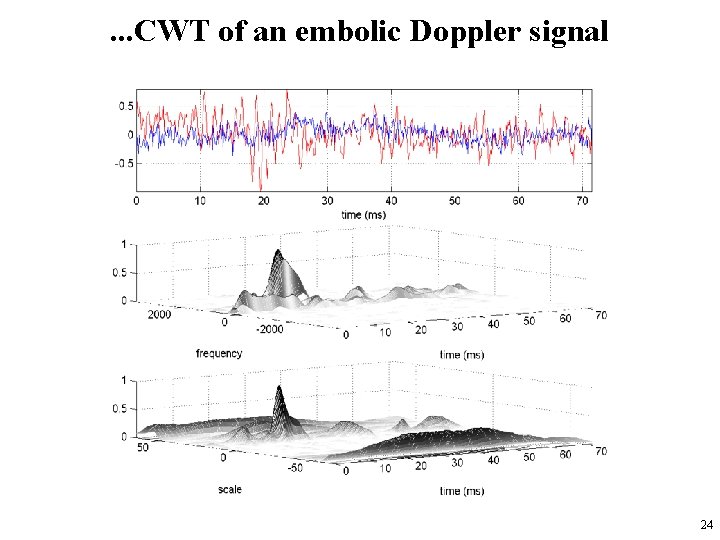
Example: analysis of Embolic Doppler signal 22

. . . CWT of an embolic Doppler signal. . . 23

. . . CWT of an embolic Doppler signal 24

04 Aralik 2 k 12 Discrete Wavelet Transform 25

Discrete Wavelet Transform (DWT) • Discrete WT is a special case of the continuous WT when a=a 0 j and b=n. a 0 j. • Dyadic wavelet bases are obtained when a 0=2 26

Discrete Wavelet Transform • Scaling and positions are dyadic • Fast algorithms exist • Scaling function and wavelet must satisfy the following conditions 27

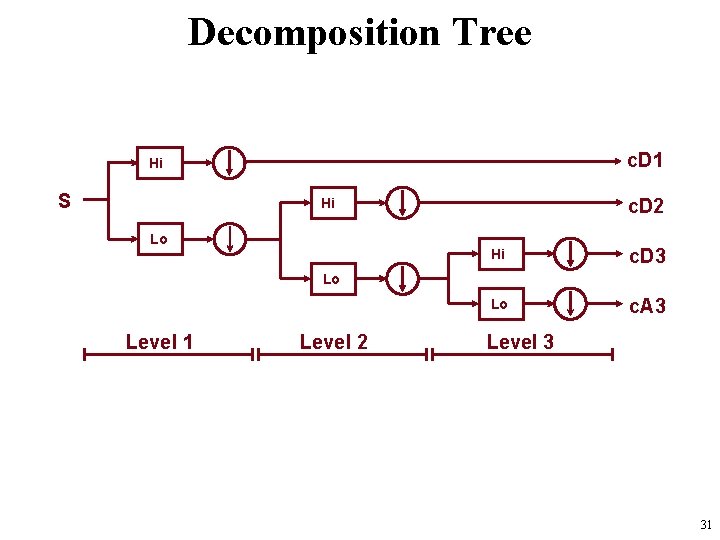
Discrete Wavelet Transform • CWT: Scales = any value • DWT: Scales = Dyadic scale 21 22 23 24 25. . . • Equivalent to: Signal Detail (level 1) Approximation (level 1) Detail (level 2) Approximation (level 2) S = D 1 + A 1 = D 1 + D 2 + A 2 28

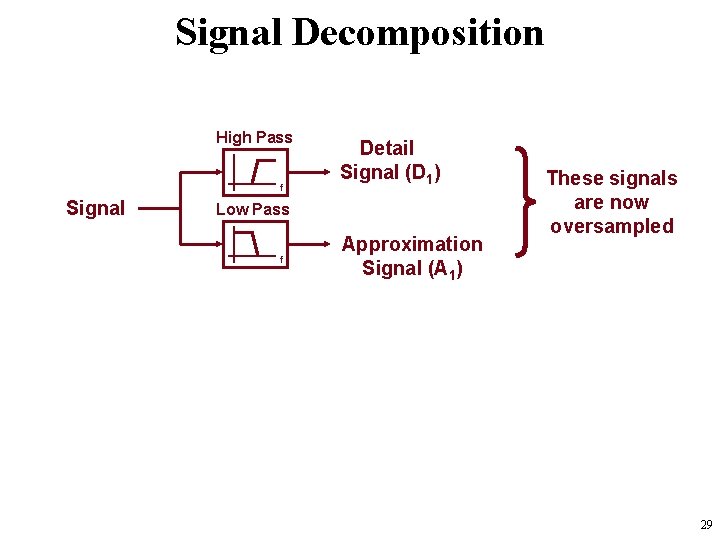
Signal Decomposition High Pass f Signal Detail Signal (D 1) Low Pass f Approximation Signal (A 1) These signals are now oversampled 29

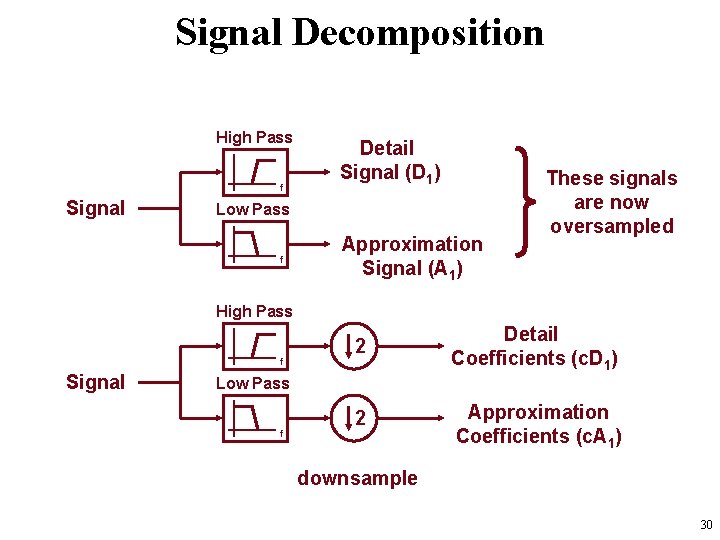
Signal Decomposition High Pass f Signal Detail Signal (D 1) Low Pass f Approximation Signal (A 1) These signals are now oversampled High Pass f Signal 2 Detail Coefficients (c. D 1) 2 Approximation Coefficients (c. A 1) Low Pass f downsample 30

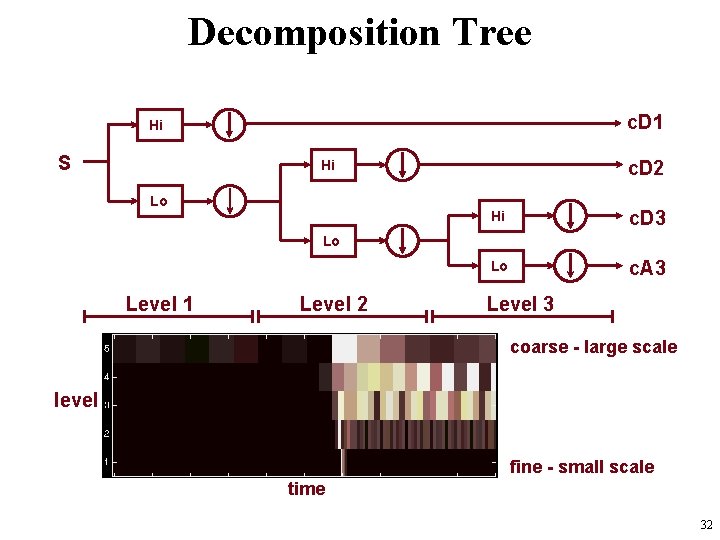
Decomposition Tree c. D 1 Hi S c. D 2 Hi Lo Hi c. D 3 Lo c. A 3 Lo Level 1 Level 2 Level 3 31

Decomposition Tree c. D 1 Hi S c. D 2 Hi Lo Hi c. D 3 Lo c. A 3 Lo Level 1 Level 2 Level 3 coarse - large scale level fine - small scale time 32

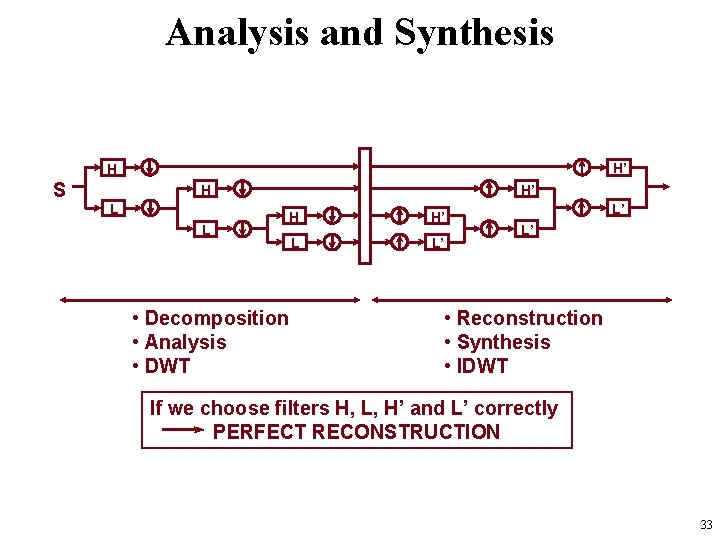
Analysis and Synthesis H’ H S H’ H L L • Decomposition • Analysis • DWT H H’ L L’ L’ L’ • Reconstruction • Synthesis • IDWT If we choose filters H, L, H’ and L’ correctly PERFECT RECONSTRUCTION 33

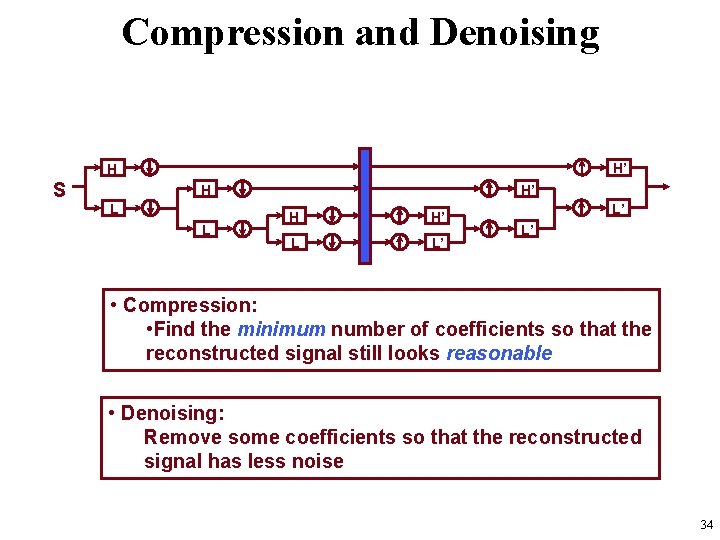
Compression and Denoising H’ H S H’ H L L H H’ L L’ L’ L’ • Compression: • Find the minimum number of coefficients so that the reconstructed signal still looks reasonable • Denoising: Remove some coefficients so that the reconstructed signal has less noise 34

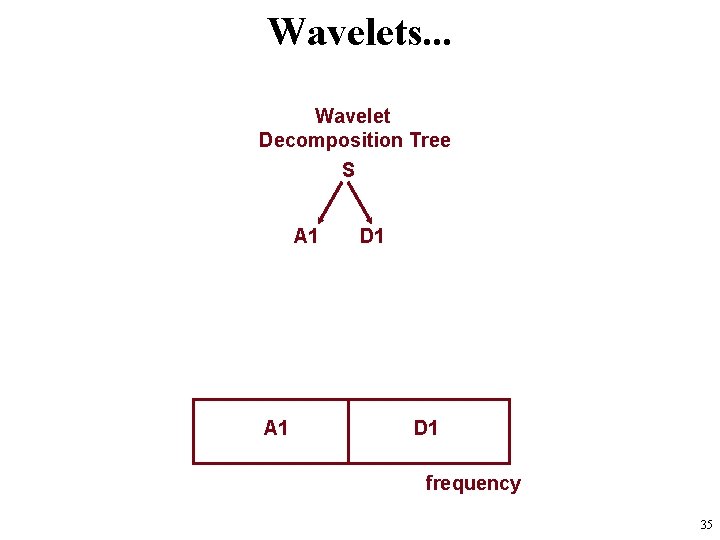
Wavelets. . . Wavelet Decomposition Tree S A 1 D 1 frequency 35

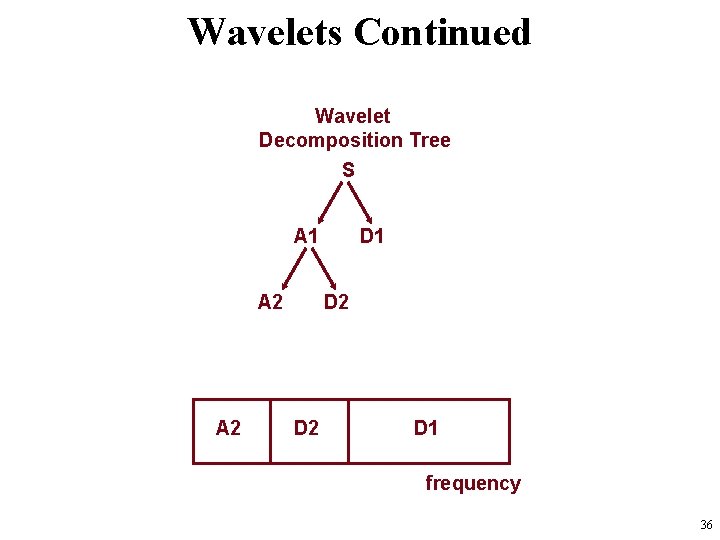
Wavelets Continued Wavelet Decomposition Tree S A 1 A 2 D 1 D 2 D 1 frequency 36

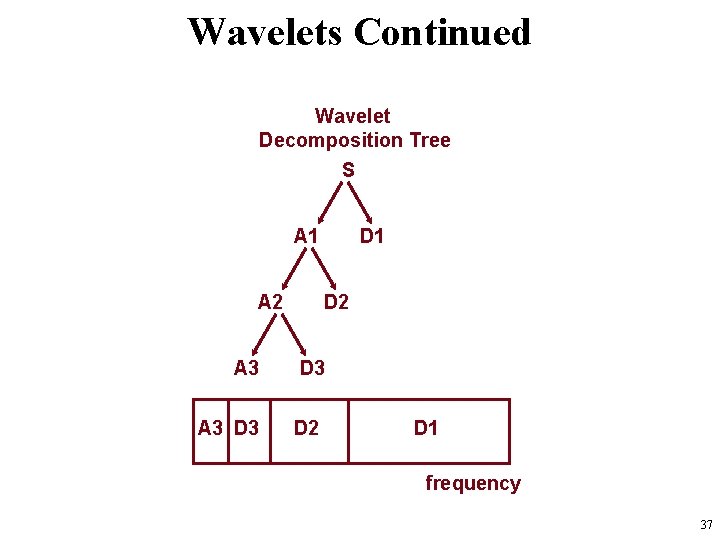
Wavelets Continued Wavelet Decomposition Tree S A 1 A 2 D 1 D 2 A 3 D 3 D 2 D 1 frequency 37

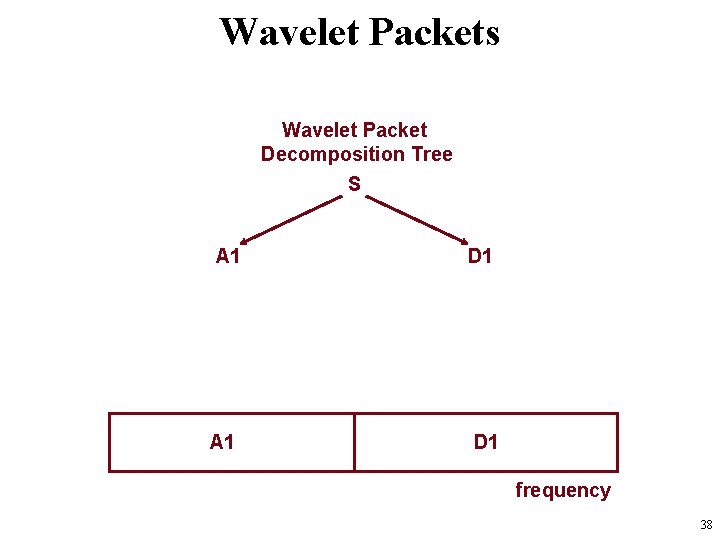
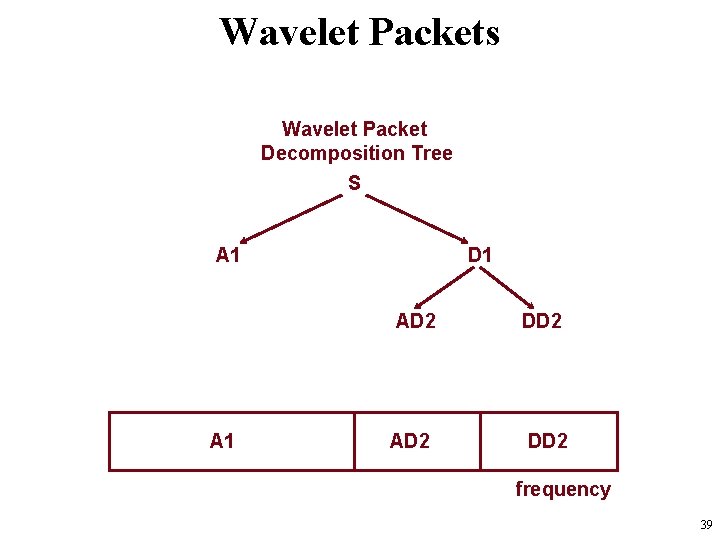
Wavelet Packets Wavelet Packet Decomposition Tree S A 1 D 1 frequency 38

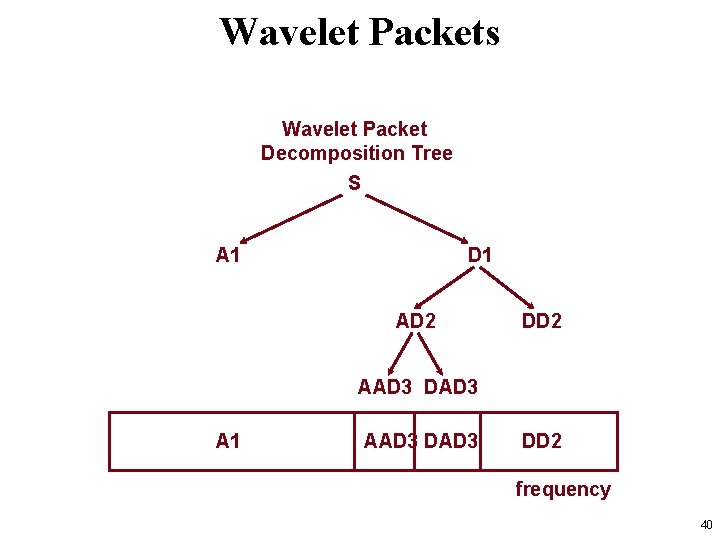
Wavelet Packets Wavelet Packet Decomposition Tree S A 1 D 1 AD 2 DD 2 frequency 39

Wavelet Packets Wavelet Packet Decomposition Tree S A 1 D 1 AD 2 DD 2 AAD 3 DAD 3 A 1 AAD 3 DD 2 frequency 40

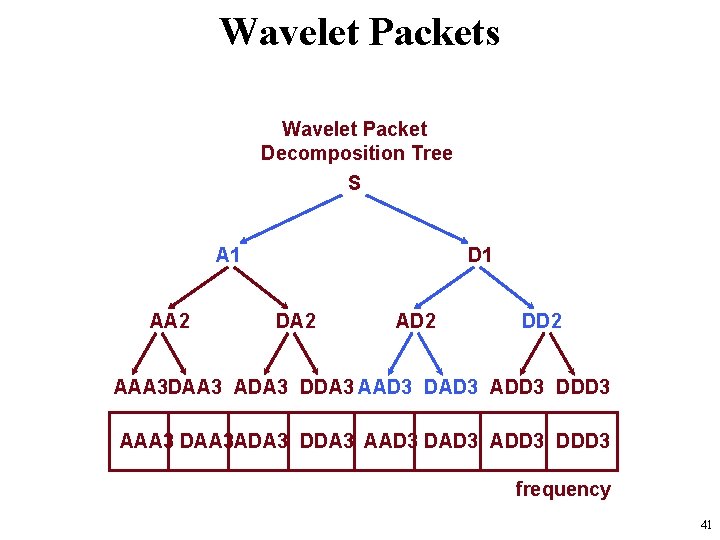
Wavelet Packets Wavelet Packet Decomposition Tree S A 1 AA 2 D 1 DA 2 AD 2 DD 2 AAA 3 DAA 3 ADA 3 DDA 3 AAD 3 DAD 3 ADD 3 DDD 3 AAA 3 DAA 3 ADA 3 DDA 3 AAD 3 DAD 3 ADD 3 DDD 3 frequency 41

42