A Survey on the 3 Decomposition Conjecture Arthur

A Survey on the 3 -Decomposition Conjecture Arthur Hoffmann-Ostenhof, Technical University of Vienna Pilsen, 2015

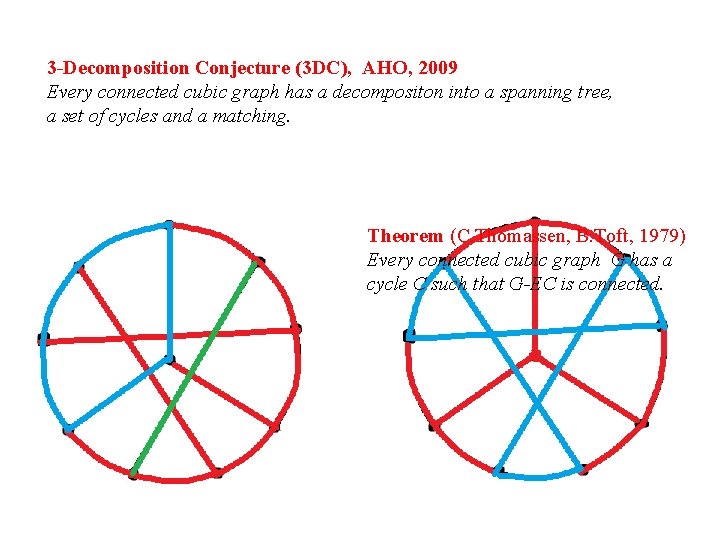
3 -Decomposition Conjecture (3 DC), AHO, 2009 Every connected cubic graph has a decompositon into a spanning tree, a set of cycles and a matching. Theorem (C. Thomassen, B. Toft, 1979) Every connected cubic graph G has a cycle C such that G-EC is connected.

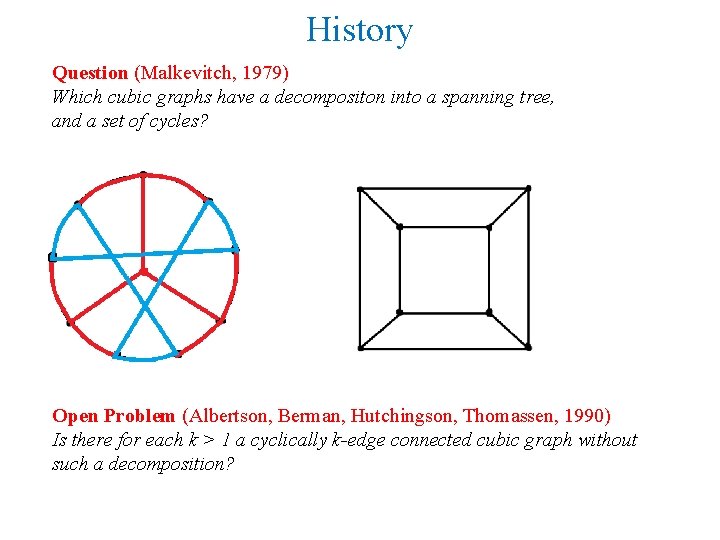
History Question (Malkevitch, 1979) Which cubic graphs have a decompositon into a spanning tree, and a set of cycles? Open Problem (Albertson, Berman, Hutchingson, Thomassen, 1990) Is there for each k > 1 a cyclically k-edge connected cubic graph without such a decomposition?

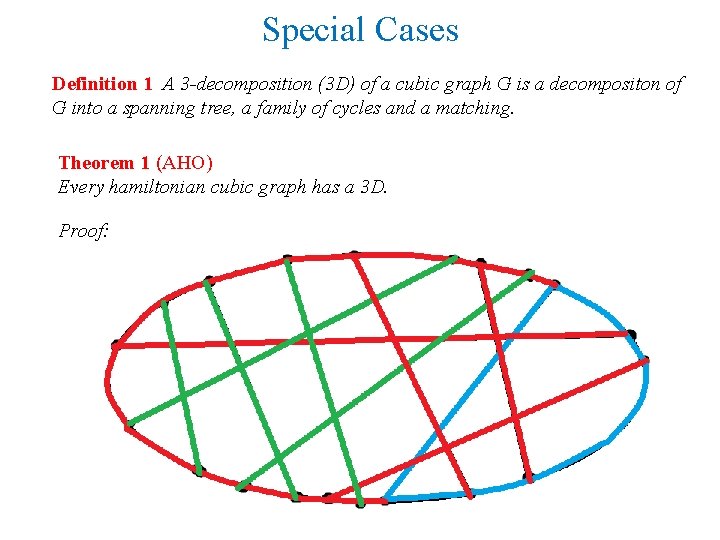
Special Cases Definition 1 A 3 -decomposition (3 D) of a cubic graph G is a decompositon of G into a spanning tree, a family of cycles and a matching. Theorem 1 (AHO) Every hamiltonian cubic graph has a 3 D. Proof:

Best Results Theorem 2 (K. Ozeki, D. Ye, 2014) Every 3 -connected cubic plane graph has a 3 D. Every 3 -connected cubic graph embedded on the projective plane has a 3 D. Theorem 3 (A. Bachstein, D. Ye, 2015) Every 3 -connected cubic graph embedded on the torus has a 3 D. Every 3 -connected cubic graph embedded on the Klein bottle has a 3 D.

Variations of the 3 DC 3 -Decomposition Conjecture (3 DC) Every connected cubic graph has a 3 D, i. e. a decompositon into a spanning tree, a set of cycles and a matching. Strong-3 DC Let G be a connected cubic graph and C be a 2 -regular subgraph of G such that G-EC is connected. Then there is a 3 D of G such that the set of cycles of the 3 D contains every cycle of C. Theorem 4 (AHO) The Strong-3 DC and the 3 DC are equivalent.

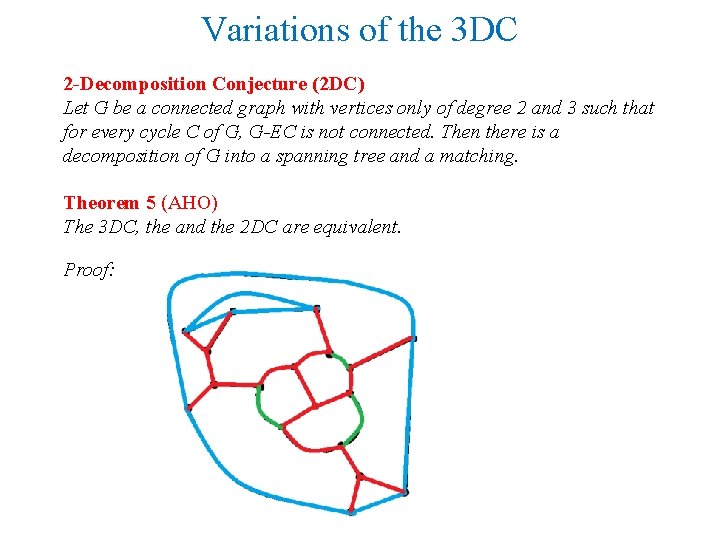
Variations of the 3 DC 2 -Decomposition Conjecture (2 DC) Let G be a connected graph with vertices only of degree 2 and 3 such that for every cycle C of G, G-EC is not connected. Then there is a decomposition of G into a spanning tree and a matching. Theorem 5 (AHO) The 3 DC, the and the 2 DC are equivalent. Proof:

Related Results (2 DC) 2 -Decomposition Conjecture (2 DC) Let G be a connected graph with vertices only of degree 2 and 3 such that for every cycle C of G, G-EC is not connected. Then there is a decomposition of G into a spanning tree and a matching. Theorem 6 (Y. Wang and Q. Zhang, 2011) Every planar graph with girth at least 8 has a 2 D.

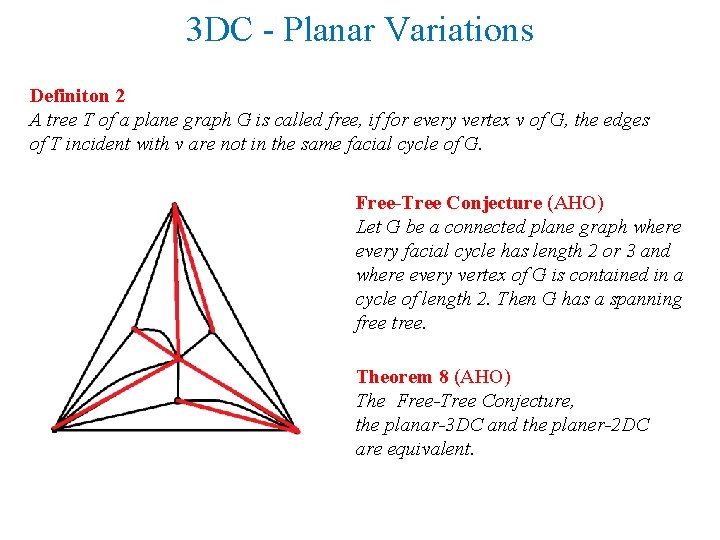
3 DC - Planar Variations Definiton 2 A tree T of a plane graph G is called free, if for every vertex v of G, the edges of T incident with v are not in the same facial cycle of G. Free-Tree Conjecture (AHO) Let G be a connected plane graph where every facial cycle has length 2 or 3 and where every vertex of G is contained in a cycle of length 2. Then G has a spanning free tree. Theorem 8 (AHO) The Free-Tree Conjecture, the planar-3 DC and the planer-2 DC are equivalent.

THANKS FOR YOUR ATTENTION

Generalized Question for graphs with higher vertex degree Which graphs have a HIST? (Homeomorphically Irreducible Spanning Tree) Theorem (Albertson, Berman, Hutchingson, Thomassen; 1990) Every connected graph G with n vertices has a HIST if δ(G) is at least 4(2 n)^1/2. Theorem (Lemke, 1988) It is NP-complete to determine whether a given cubic graph has a decomposition into a spanning tree and cycles. .