2 7 Rekursio ja iteraatio Algoritminen ongelmanratkaisu ei

2. 7 Rekursio ja iteraatio Algoritminen ongelmanratkaisu ei ole läheskään aina triviaalien moduuleiden kirjoittamista. Ongelman ratkaisun ydin perustuu usein sopivan toisto-osan löytymiseen. Toiston ohjelmointiin on kaksi näennäisesti erilaista ratkaisutapaa: rekursio ja iteraatio

2. 7 Rekursio ja iteraatio … Rekursiivinen moduuli sisältää moduulin itsensä kutsun ja iteratiivinen moduuli sisältää toistorakenteen. Rekursio ja iteraatio ovat keinoja etsiä ongelmanratkaisuja algoritmien suunnittelumenetelmien (esim. top-down) ’sisällä’.

2. 7 Rekursio ja iteraatio … MODULE maalaa (aita) WHILE aitaa maalamatta DO suorita laudan maalaus siirry seuraavaan lautaan ENDWHILE ENDMODULE ITERAATIO MODULE maalaa (aita) IF aitaa maalamatta THEN suorita laudan maalaus maalaa (loput aidasta) ENDIF ENDMODULE REKURSIO

2. 7. 1 Rekursio MODULE maalaa (aita) ITERAATIO WHILE aitaa maalamatta DO suorita laudan maalaus siirry seuraavaan lautaan ENDWHILE ENDMODULE maalaa (aita) REKURSIO IF aitaa maalamatta THEN suorita laudan maalaus maalaa (loput aidasta) ENDIF ENDMODULE

2. 7. 1 Rekursio… Rekursio on modulaarisuusperiaatteen suora seuraus, eikä suinkaan mikään erillinen ominaisuus tai sallittu temppu. Rekursio on yleisen ongelmanratkaisuperiaatteen, reduktioperiaatteen erikoistapaus. Reduktiota sanotaan rekursioksi, jos ainakin yksi osaongelma on alkuperäisen ongelman kaltainen.

2. 7. 1 Rekursio … Jotta menettely suppenisi eli johtaisi todella ratkaisuun tulee rekursiivisen aliongelman luonnollisestikin olla ongelman alkuperäistä tapausta yksinkertaisempi.

2. 7. 1 Rekursio … Rekursiivisten moduulien konstruoimisessa on huomattava kaksi seikkaa: 1. Moduulissa pitää kuvata ainakin yksi ongelman triviaali tapaus, joka ratkeaa suoraan, siis ei-rekursiivisesti, ja 2. Jokaisen rekursiivisen kutsun tulee lähestyä jotakin tällaista triviaalia tapausta

2. 7. 1 Rekursio … Kaikissa ohjelmointikielissä rekursiota ei ole mahdollista toteuttaa (mm. konekielet, eräät vanhat tehtävän läheiset kielet kuten Basic, Fortran, Cobol)

2. 7. 1 Rekursio … Jos moduuli kutsuu itseään, on kyseessä suora rekursio. Tämä on tyypillisin tapaus rekursiosta. Esim. aidan maalaus. Epäsuora rekursio: jokin osaongelma sisältää rekursiivisen kutsun.

2. 7. 1 Rekursio … Epäsuoran rekursion esimerkki: MODULE M 1 … M 2 … ENDMODULE M 2 … … M 1 … ENDMODULE Epäsuora rekursio tekee algoritmeista vaikeasti ymmärrettäviä ei suositella.

2. 7. 1 Rekursio … Rekursioesimerkkejä monisteessa.

2. 7. 2 Iteraatioperiaate tarkoittaa sitä, että jotakin toimenpidettä toistamalla päästään yhä lähemmäksi ratkaisua tai asetettua tavoitetta. Tarkoitus on siis tuottaa yhä parempia ja parempia ratkaisuja, ns. välitiloja tai likiarvoja ongelman ratkaisulle. Prosessi päättyy, kun saadaan joko tarkka ratkaisu tai riittävän tarkka likiarvo.

2. 7. 2 Iteraation soveltamiselle asetaan kolme vaatimusta: väliarvojen olemassaolo keino edetä kohti ratkaisua kyky tunnistaa ratkaisu (ts. pitää tietää milloin toisto lopetetaan).

2. 7. 2 Iteraatio … Esimerkiksi järjestä-moduulissa: vaadittavat välitilat ovat lukujonon eri järjestykset kullakin ulomman silmukan toistokerralla päästään yhä lähemmäksi ratkaisua: jono on oikeassa järjestyksessä alusta lukien i: nteen alkioon saakka, i = 1, 2, … n-1. tarkka ratkaisu on saavutettu, kun i = n-1.

2. 7. 2 Iteraatio … Iteraatio on luonteva lähestymistapa tehtävissä, jossa ei välttämättä saada tarkkaa ratkaisua, vaan on tyydyttävä likarvoon. Monet numeerisen analyysin menetelmät ovat tällaisia.

2. 7. 2 Iteraatio … Esimerkki: neliöjuuri, √a = ? Newtonin menetelmä: oletetaan, että luvun neliöjuuri = 1 (merk. x 1). Lasketaan sitten ns. Newtonin kaavalla aina uusia ja uusia x-arvoja: x 2, x 3, …. Seuraava x-arvo on edeltäjäänsä lähempänä √a : n arvoa. Kaava: xn = ½(xn-1 + a/xn-1), n > 1.

2. 7. 2 Iteraatio … Esimerkki: neliöjuuri jatkuu MODULE neliöjuuri (a, eps) RETURNS √a n: =1 x 1: =1 REPEAT xn+1 = ½(xn + a/xn) n: =n+1 UNTIL xn-1 – xn < eps RETURN xn

2. 7. 2 Iteraatio … Esimerkki: neliöjuuri jatkuu, parempi versio: MODULE neliöjuuri (a, eps) RETURNS √a nykyinen: =1 REPEAT edellinen: =nykyinen: = ½(edellinen + a/edellinen) UNTIL edellinen-nykyinen < eps RETURN nykyinen ENDMODULE

2. 7. 2 Iteraatio … Menetelmä on tehokas ja yksinkertainen. Esimerkiksi, jos a = 10 000, kahdeksan numeron tarkkuus saavutetaan jo yhdeksällä kierroksella.

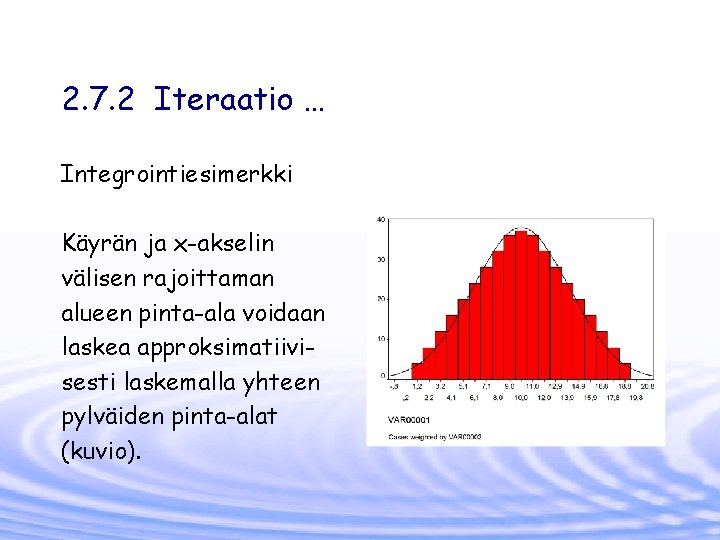
2. 7. 2 Iteraatio … Integrointiesimerkki Käyrän ja x-akselin välisen rajoittaman alueen pinta-ala voidaan laskea approksimatiivisesti laskemalla yhteen pylväiden pinta-alat (kuvio).

2. 7. 2 Iteraatio … MODULE integroi (f, a, b) RETURNS luku I: =0 n: =9999 (* n: n arvoksi suuri luku *) dx: =(b-a)/n FOR x: =0, 1, 2, …, n-1 DO I: =I+f(a+x*dx) ENDFOR RETURN I*dx ENDMODULE

2. 7. 2 Iteraatio … Eratostheneen (276 -195 e. Kr. ) seula etsii alkulukuja: MODULE seula (n) RETURNS alkulukujen joukko S: = {2, 3, 4, 5, 6, …, n} A: = Ø (* tyhjä joukko *) REPEAT Etsi joukon S pienin luku b A: =A U {b} (* alkio b lisätään joukkoon A *) m: =b REPEAT S: =S- {m} (* poistetaan m joukosta S*) m: =m+b UNTIL m > n UNTIL b > √n RETURN A U S ENDMODULE

2. 7. 3 Rekursio vai iteraatio ? Rekursio ja iteraatio ovat vaihtoehtoisia strategioita. Jokainen rekursiivinen algoritmi voidaan muuntaa iteratiiviseksi ja päinvastoin. Imperatiivisessa ajattelussa iteraatio on varsin tavallinen ajattelutapa, koska kyseinen työskentelytapa on lähellä tietokoneen toimintamallia. Rekursio puolestaan perustuu modulaarisuuteen ja reduktiiviseen ajatteluun, joka taas on luonteenomaista esim. funktionaalisessa ohjelmoinnissa.

Rekursio vai iteraatio ? …. Jotkin tehtävät ovat sellaisia, että niille on kohtuullisen helposti löydettävissä joko rekursiivinen tai iteratiivinen ratkaisu mutta ei molempia. On myös tehtäviä, joille ei olemassa luonnollista ei-rekursiivista ratkaisua, kyseessä ovat ns. ei-rekursiiviset tehtävät.

Rekursio vai iteraatio ? … Seuraavat kaksi esimerkkiä ratkeavat varsin helposti rekursion kautta. Iteratiivinen ratkaisukin on olemassa, mutta se on hankala keksiä: symbolinen derivointi Hanoin tornit