10 Parametric Equations and Polar Coordinates Copyright Cengage


















- Slides: 19

10 Parametric Equations and Polar Coordinates Copyright © Cengage Learning. All rights reserved.

10. 4 Areas and Lengths in Polar Coordinates Copyright © Cengage Learning. All rights reserved.

Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the area of a sector of a circle: A = r 2 where, as in Figure 1, r is the radius and is the radian measure of the central angle. Figure 1 3

Areas and Lengths in Polar Coordinates Formula 1 follows from the fact that the area of a sector is proportional to its central angle: A = ( /2 ) r 2 = r 2. 4

Areas and Lengths in Polar Coordinates Let be the region, illustrated in Figure 2, bounded by the polar curve r = f ( ) and by the rays = a and = b, where f is a positive continuous function and where 0 < b – a 2. Figure 2 We divide the interval [a, b] into subintervals with endpoints 0, 1, 2, . . . , n and equal width . 5

Areas and Lengths in Polar Coordinates The rays = i then divide into n smaller regions with central angle = i – 1. If we choose in the ith subinterval [ i – 1, i], then the area Ai of the ith region is approximated by the area of the sector of a circle with central angle and radius f ( ). (See Figure 3. ) Figure 3 6

Areas and Lengths in Polar Coordinates Thus from Formula 1 we have Ai [f ( )]2 and so an approximation to the total area A of is It appears from Figure 3 that the approximation in (2) improves as n . 7

Areas and Lengths in Polar Coordinates But the sums in (2) are Riemann sums for the function g( ) = [f ( )]2, so It therefore appears plausible that the formula for the area A of the polar region is 8

Areas and Lengths in Polar Coordinates Formula 3 is often written as with the understanding that r = f ( ). Note the similarity between Formulas 1 and 4. When we apply Formula 3 or 4 it is helpful to think of the area as being swept out by a rotating ray through O that starts with angle a and ends with angle b. 9

Example 1 Find the area enclosed by one loop of the four-leaved rose r = cos 2. Solution: Notice from Figure 4 that the region enclosed by the right loop is swept out by a ray that rotates from = – /4 to = /4. Figure 4 10

Example 1 – Solution cont’d Therefore Formula 4 gives 11

Example 1 – Solution cont’d 12

Arc Length 13

Arc Length To find the length of a polar curve r = f ( ), a b, we regard as a parameter and write the parametric equations of the curve as x = r cos = f ( ) cos y = r sin = f ( ) sin Using the Product Rule and differentiating with respect to , we obtain 14

Arc Length So, using cos 2 + sin 2 = 1, we have 15

Arc Length Assuming that f is continuous, we can write the arc length as Therefore the length of a curve with polar equation r = f ( ), a b, is 16

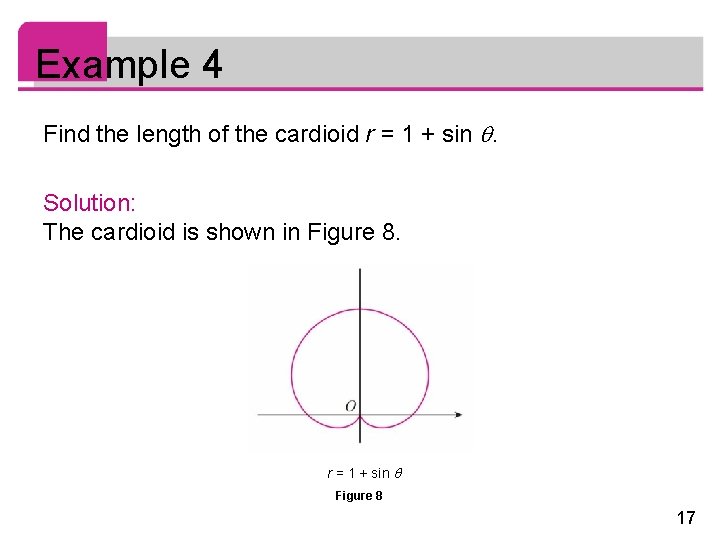
Example 4 Find the length of the cardioid r = 1 + sin . Solution: The cardioid is shown in Figure 8. r = 1 + sin Figure 8 17

Example 4 – Solution cont’d Its full length is given by the parameter interval 0 2 , so Formula 5 gives 18

Example 4 – Solution cont’d We could evaluate this integral by multiplying and dividing the integrand by , or we could use a computer algebra system. In any event, we find that the length of the cardioid is L = 8. 19
 Polar curve
Polar curve Polar derivative
Polar derivative Bmk+
Bmk+ Parametric test
Parametric test Parametric and non parametric algorithms
Parametric and non parametric algorithms Parametric vs non parametric test
Parametric vs non parametric test Difference between consecutive and independent coordinates
Difference between consecutive and independent coordinates Chapter 7 conic sections and parametric equations
Chapter 7 conic sections and parametric equations Cengage chapter 7
Cengage chapter 7 Cho hang
Cho hang Polar to rectangular equation
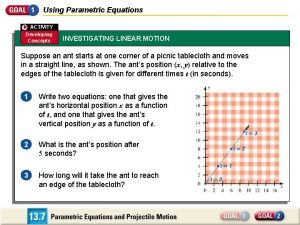
Polar to rectangular equation In a pumpkin tossing contest in morton illinois
In a pumpkin tossing contest in morton illinois Parametric equations word problems
Parametric equations word problems How to write parametric equations
How to write parametric equations Parametric motion
Parametric motion How to solve parametric equations
How to solve parametric equations Complete smith chart
Complete smith chart Parametric equations
Parametric equations Dr frost parametric equations
Dr frost parametric equations Polar curve
Polar curve