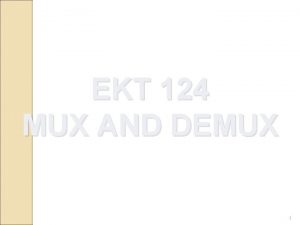Warm Up 5 124 Consider the equation x

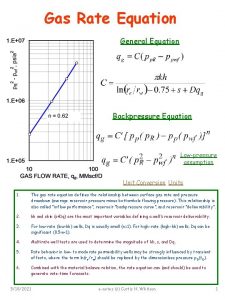
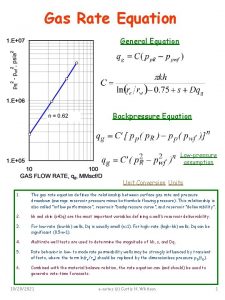
Warm Up: 5 -124. Consider the equation x 2 = 2. •

5. 2. 6 INTRODUCING COMPLEX NUMBERS February 6, 2020 HW: 5 -131 through 5 -136

Objectives • CO: SWBAT perform operations on complex numbers and solve quadratic equations with nonreal solutions. • LO: SWBAT explain what imaginary (complex) numbers are.

Historical Note: Imaginary Numbers In some ways, each person’s math education parallels the history of mathematical discovery. When you were much younger, if you were asked, “How many times does 3 go into 8? ” or “What is 8 divided by 3? ”, you might have said, “ 3 doesn’t go into 8. ” Then you learned about numbers other than whole numbers, and the question had an answer. Later, if you were asked, “What number squared equals 5? ” you might have said, “No number squared equals 5. ” Then you learned about irrational numbers, and you could answer that question. Similarly, until about 500 years ago, the answer to the question, “What number squared equals – 1? ” was, “No number squared equals – 1. ” Then something remarkable happened. An Italian mathematician named Bombelli used a formula for finding the roots of polynomials. Within the formula was a square root, and when he applied the formula, the number under the square root came out negative. Instead of giving up, he had a brilliant idea. He had already figured out that the equation had a solution, so he decided to see what would happen if he pretended that there was a number he could square to make a negative. Remarkably, he was able to continue the calculation, and eventually the “imaginary” number disappeared from the solution. More importantly, the resulting answer worked; it solved his original equation. This led to the acceptance of these so-called imaginary numbers. The name stuck, and mathematicians became convinced that all quadratic equations do have solutions. Of course, in some situations you will only be interested in real number solutions (that is, solutions not having an imaginary part).

• 4 s lead a 3 s lead b 2 s lead c 1 s lead d

5 -127. Graph the function f(x) = x 2 − 4 x + 5 on your calculator. • Team

5 -128. In problem 5 -127, you found the solutions to a quadratic equation x 2 − 4 x + 5 = 0. The roots of a polynomial function f(x) are the values of x such that f(x) = 0. You have seen that solutions to equations can be real or complex, so it follows that roots can also be real or complex. Compare & contrast what happens with the graphs & equations for the three cases in parts (a) through (c) below. a. Sketch the graph of f(x) = (x + 3)2 − 4. Use the graph to determine the roots of f(x). x = – 1 and – 5 4 b. Sketch the graph of g(x) = (x + 3)2. What are the roots of g(x)? x = – 3 Team 3 c. Sketch the graph of h(x) = (x + 3) + 4. Can you determine the roots of h(x) by at the graph? Why or why not? 2 No, looking because it does not cross the x-axis 2 d. Determine the roots of h(x) = (x + 3)2 + 4 by solving an equation. Write your answers as complex numbers. 1 x = − 3 + 2 i or x = − 3 − 2 i e. Describe in words the relationship between the graphs of parabolas and the kinds of roots their equations have. If the graph crosses the x‑axis, the equation has real roots. If the graph does not cross the x‑axis, the equation has complex roots, and if the graph only touches the x‑axis, there is only one real root.

5 -129. The sum of a real number and an imaginary number, such as 2 + 3 i, is called a complex number. A complex number can be written in the form a + bi, where a and b are both real numbers. Use the definition of i and your understanding of real numbers to rewrite each of the following expressions. a. 2(3 + i) b. 10 – 9 i – i c. (– 2 – 7 i) + (– 1 + 4 i) d. (– 8 + 2 i) – (1 – 6 i) e. (1 – i)(8 – 6 i) Pairs Check

TINYURL. COM/NIEVES-M 2 -526