Translating Verbal Expressions When translating a verbal expression

Translating Verbal Expressions

When translating a verbal expression into a math statement: • Read the verbal expression carefully at least 2 times. • Identify what you are looking for, or the piece that you don’t know, as the variable. • Identify the verbal clues in the expression. • Translate the words into an algebraic expression.
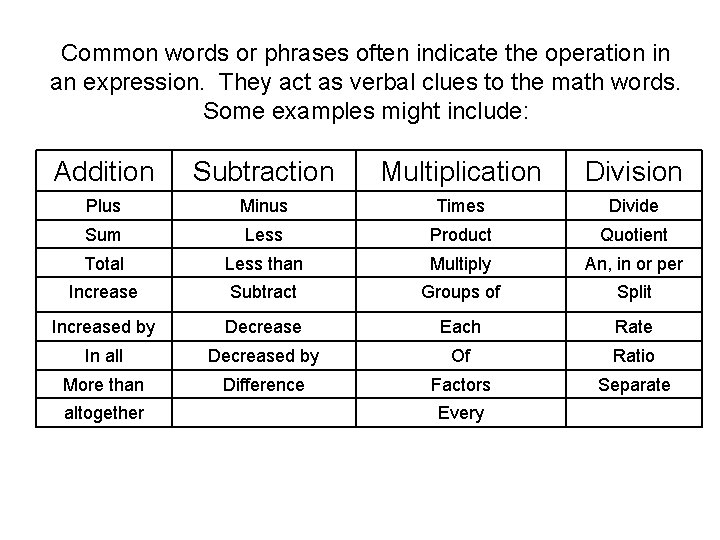
Common words or phrases often indicate the operation in an expression. They act as verbal clues to the math words. Some examples might include: Addition Subtraction Multiplication Division Plus Minus Times Divide Sum Less Product Quotient Total Less than Multiply An, in or per Increase Subtract Groups of Split Increased by Decrease Each Rate In all Decreased by Of Ratio More than Difference Factors Separate altogether Every
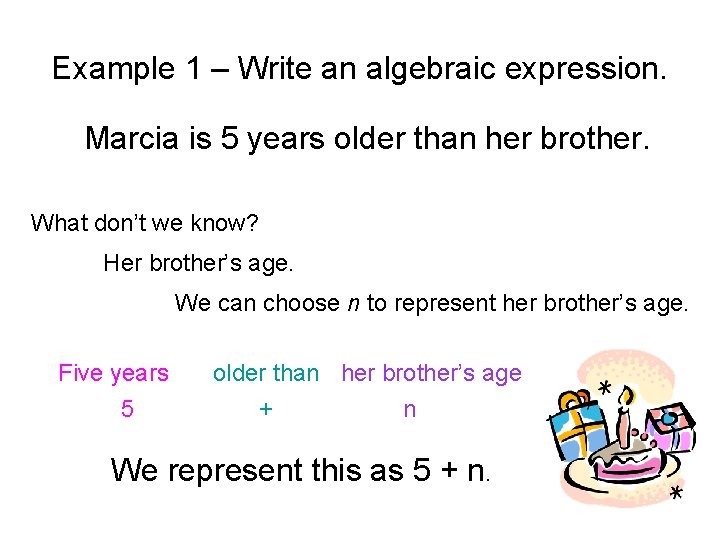
Example 1 – Write an algebraic expression. Marcia is 5 years older than her brother. What don’t we know? Her brother’s age. We can choose n to represent her brother’s age. Five years 5 older than her brother’s age + n We represent this as 5 + n.

Example 2 – Write an algebraic expression. Adam makes nine dollars every hour that he works. What don’t we know? How many hours he works. We can use h to represent the number of hours. Nine dollars every 9 ∙ hour h We represent this as 9 h.

Example 3 – Write an algebraic expression. For the magic trick, the number I chose is ten less than the number the magician chose. What don’t we know? The number the magician chose. Let’s use n to represent the magician’s number. Ten 10 less than - magician’s # n Be careful! LESS THAN IS A SWITCH PHRASE. This means you switch the order of the phrase. We represent this as n – 10.

Now your turn! 1. The difference between seven and a number. 7 -n 2. The quotient of a number and nine. n÷ 9 3. A four dollar tip is added to the bill. 4+n 4. The product of twelve and a number. 12 n 5. We scored 5 points less than the other team. n-5
- Slides: 7













