2 3 Translating Between Tables and Expressions Learn

2 -3 Translating Between Tables and Expressions Learn to write expressions for tables and sequences.

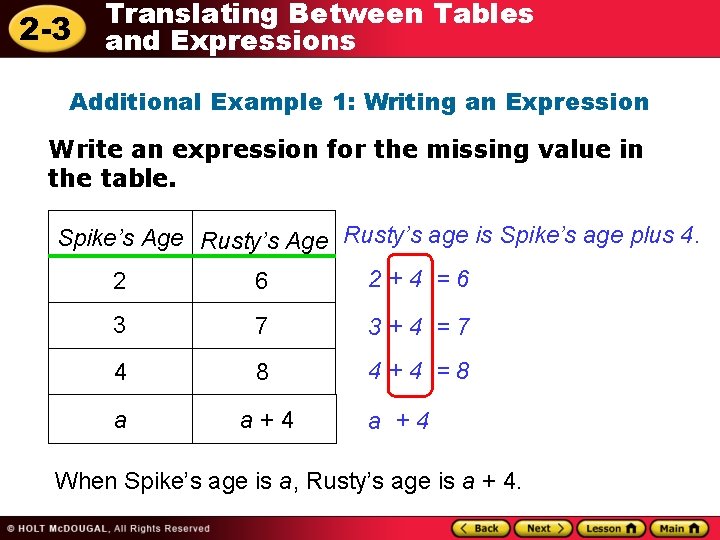
2 -3 Translating Between Tables and Expressions Additional Example 1: Writing an Expression Write an expression for the missing value in the table. Spike’s Age Rusty’s age is Spike’s age plus 4. 2 6 2+4 =6 3 7 3+4 =7 4 8 4+4 =8 a a+4 a +4 When Spike’s age is a, Rusty’s age is a + 4.

2 -3 Translating Between Tables and Expressions Check It Out: Example 1 Write an expression for the missing value in the table. Ty’s Age Rich’s age is Ty’s age times 7. 1 7 =7 2 14 2 7 = 14 3 21 3 7 = 21 a a 7 When Ty’s age is a, Rich’s age is a 7 or 7 a.

2 -3 Translating Between Tables and Expressions Additional Example 2: Writing an Expression for a Sequence Write an expression for the sequence in the table. Position 1 2 3 4 Value 7 10 13 16 n Look for a relationship between the positions and the values of the terms in the sequence. Use guess and check. Guess 7 n Guess 3 n + 4 Check by substituting 2. 7 • 2 does not equal 10. 3 • 2 + 4 = 10. The expression 3 n + 4 works for the entire sequence. 3 • 1 + 4 = 7, 3 • 2 + 4 = 10, 3 • 3 + 4 = 13, 3 • 4 + 4 = 16 The expression for the sequence is 3 n + 4.

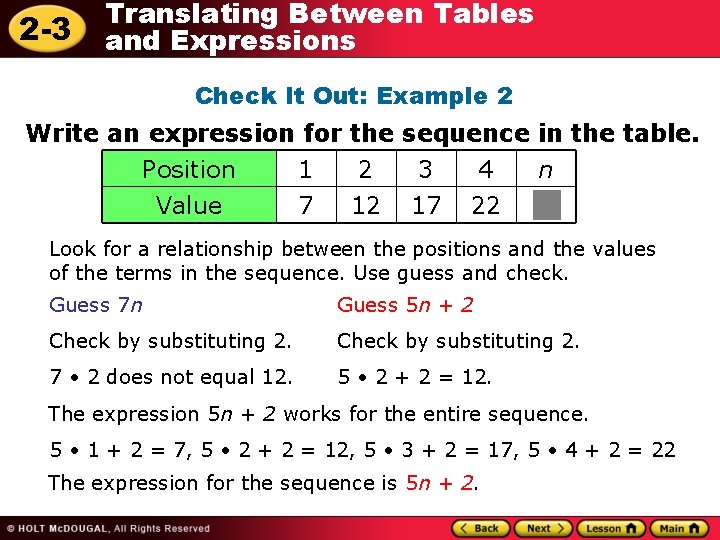
2 -3 Translating Between Tables and Expressions Check It Out: Example 2 Write an expression for the sequence in the table. Position 1 2 3 4 Value 7 12 17 22 n Look for a relationship between the positions and the values of the terms in the sequence. Use guess and check. Guess 7 n Guess 5 n + 2 Check by substituting 2. 7 • 2 does not equal 12. 5 • 2 + 2 = 12. The expression 5 n + 2 works for the entire sequence. 5 • 1 + 2 = 7, 5 • 2 + 2 = 12, 5 • 3 + 2 = 17, 5 • 4 + 2 = 22 The expression for the sequence is 5 n + 2.

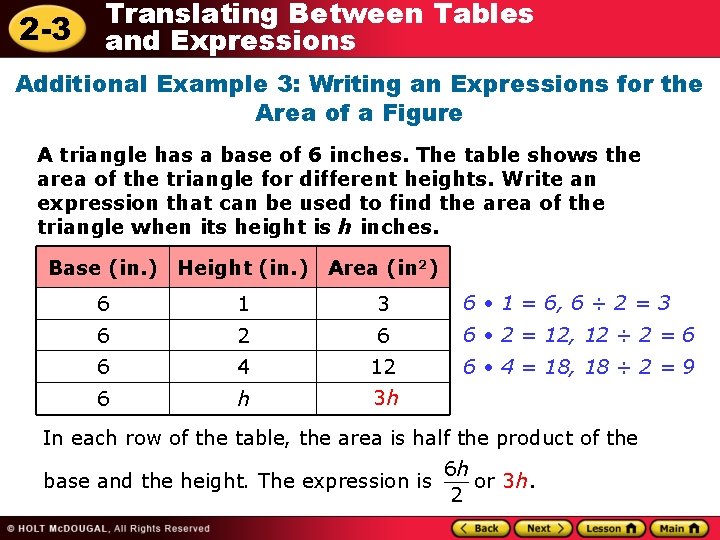
2 -3 Translating Between Tables and Expressions Additional Example 3: Writing an Expressions for the Area of a Figure A triangle has a base of 6 inches. The table shows the area of the triangle for different heights. Write an expression that can be used to find the area of the triangle when its height is h inches. Base (in. ) Height (in. ) Area (in 2) 6 1 3 6 • 1 = 6, 6 ÷ 2 = 3 6 2 6 6 • 2 = 12, 12 ÷ 2 = 6 6 4 12 6 • 4 = 18, 18 ÷ 2 = 9 6 h 3 h In each row of the table, the area is half the product of the 6 h base and the height. The expression is __ or 3 h. 2

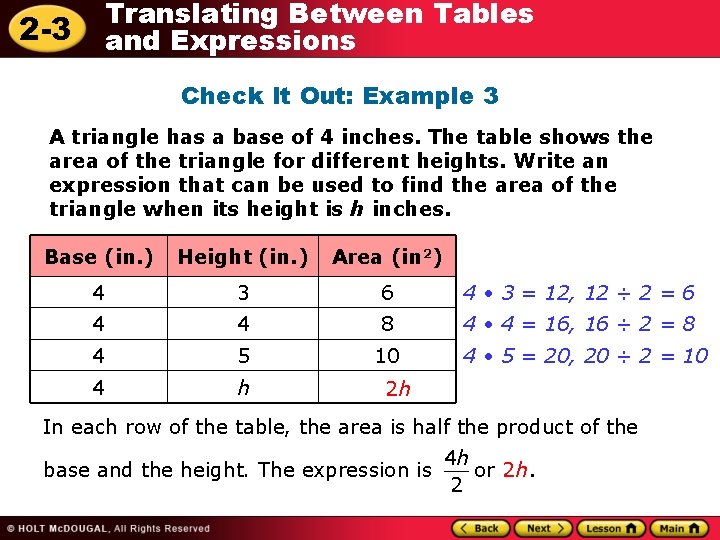
2 -3 Translating Between Tables and Expressions Check It Out: Example 3 A triangle has a base of 4 inches. The table shows the area of the triangle for different heights. Write an expression that can be used to find the area of the triangle when its height is h inches. Base (in. ) Height (in. ) Area (in 2) 4 3 6 4 • 3 = 12, 12 ÷ 2 = 6 4 4 8 4 • 4 = 16, 16 ÷ 2 = 8 4 5 10 4 h 4 • 5 = 20, 20 ÷ 2 = 10 2 h In each row of the table, the area is half the product of the 4 h base and the height. The expression is __ or 2 h. 2