TEOREMI DI PITAGORA E EUCLIDE A cura di

TEOREMI DI PITAGORA E EUCLIDE A cura di Mimmo CORRADO

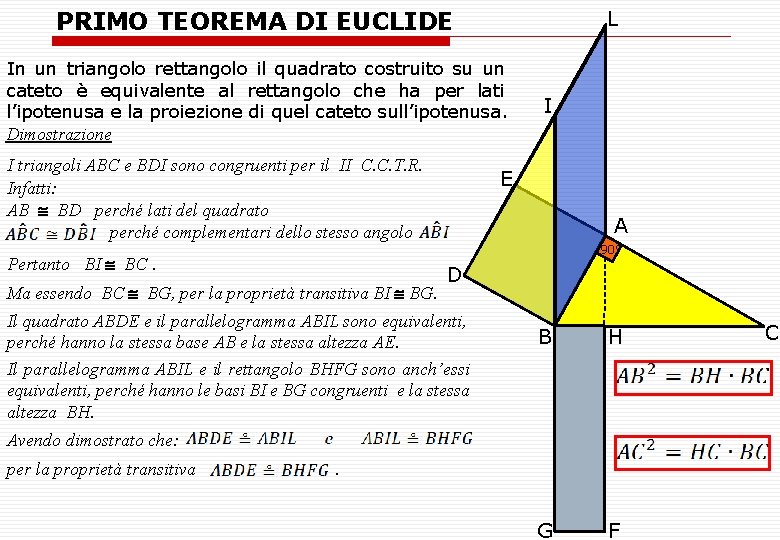
L PRIMO TEOREMA DI EUCLIDE In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha per lati l’ipotenusa e la proiezione di quel cateto sull’ipotenusa. Dimostrazione I triangoli ABC e BDI sono congruenti per il II C. C. T. R. Infatti: AB BD perché lati del quadrato perché complementari dello stesso angolo Pertanto BI BC. Ma essendo BC BG, per la proprietà transitiva BI BG. I E A 90° D Il quadrato ABDE e il parallelogramma ABIL sono equivalenti, perché hanno la stessa base AB e la stessa altezza AE. Il parallelogramma ABIL e il rettangolo BHFG sono anch’essi equivalenti, perché hanno le basi BI e BG congruenti e la stessa altezza BH. B H G F Avendo dimostrato che: per la proprietà transitiva . C

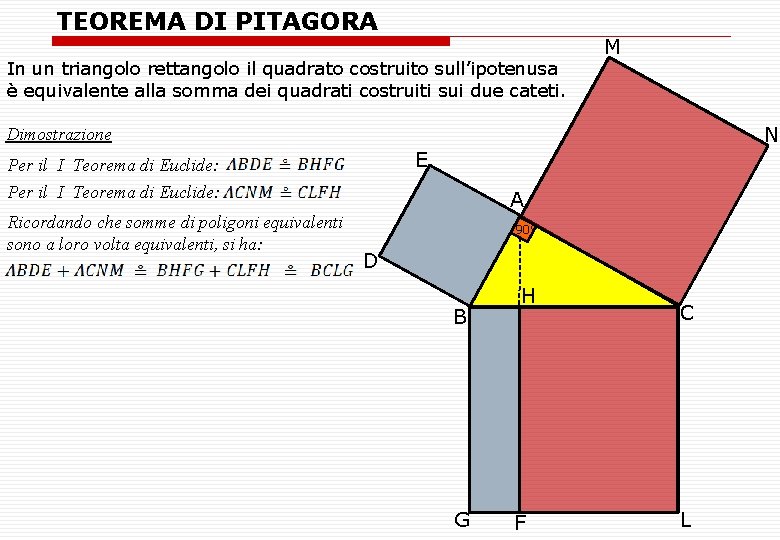
TEOREMA DI PITAGORA In un triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui due cateti. M N Dimostrazione E Per il I Teorema di Euclide: Ricordando che somme di poligoni equivalenti sono a loro volta equivalenti, si ha: A 90° D B G H F C L

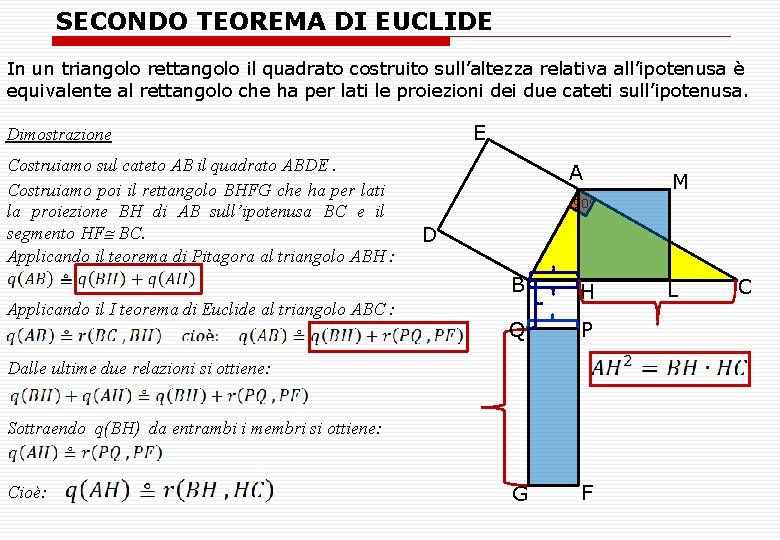
SECONDO TEOREMA DI EUCLIDE In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei due cateti sull’ipotenusa. E Dimostrazione Costruiamo sul cateto AB il quadrato ABDE. Costruiamo poi il rettangolo BHFG che ha per lati la proiezione BH di AB sull’ipotenusa BC e il segmento HF BC. Applicando il teorema di Pitagora al triangolo ABH : Applicando il I teorema di Euclide al triangolo ABC : A 90° D B H Q P G F Dalle ultime due relazioni si ottiene: Sottraendo q(BH) da entrambi i membri si ottiene: Cioè: M L C