Symtrie centrale 1 Symtrique dune figure par rapport


- Slides: 5

Symétrie centrale. 1. Symétrique d’une figure par rapport à un point. 2. Tracer des symétriques. 3. Les propriétés de la symétrie centrale. 4. Centre de symétrie d’une figure.

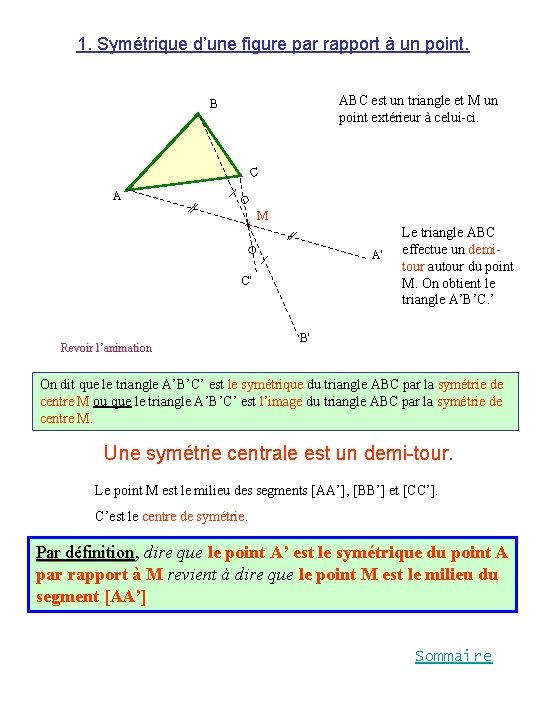
1. Symétrique d’une figure par rapport à un point. ABC est un triangle et M un point extérieur à celui-ci. B C A M A' C' Revoir l’animation Le triangle ABC effectue un demitour autour du point M. On obtient le triangle A’B’C. ’ B' On dit que le triangle A’B’C’ est le symétrique du triangle ABC par la symétrie de centre M ou que le triangle A’B’C’ est l’image du triangle ABC par la symétrie de centre M. Une symétrie centrale est un demi-tour. Le point M est le milieu des segments [AA’], [BB’] et [CC’]. C’est le centre de symétrie Par définition, définition dire que le point A’ est le symétrique du point A par rapport à M revient à dire que le point M est le milieu du segment [AA’] Sommaire

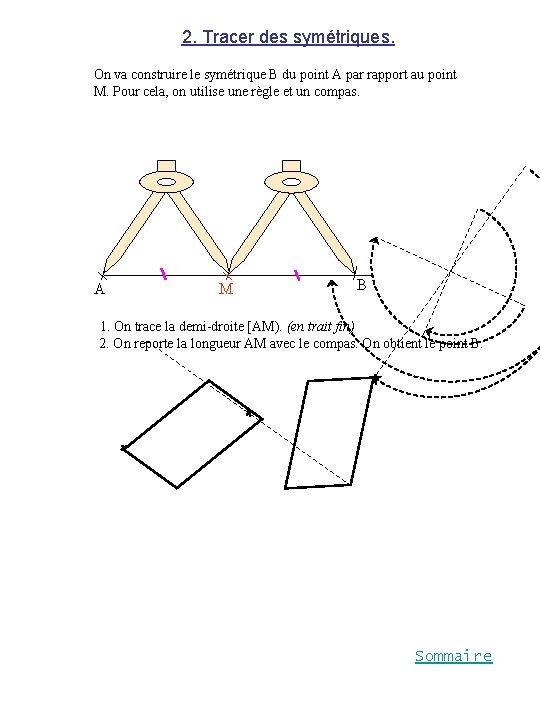
2. Tracer des symétriques. On va construire le symétrique B du point A par rapport au point M. Pour cela, on utilise une règle et un compas. A M B 1. On trace la demi-droite [AM). (en trait fin) 2. On reporte la longueur AM avec le compas. On obtient le point B. Sommaire

3. Les propriétés de la symétrie centrale. Symétrique d’un segment. Si deux segments sont symétriques par rapport à un point alors ils ont la même longueur Ici les segments [AB] et [A’B’] sont symétrique par rapport à M donc AB = A’B’. Symétrique d’une droite. Si deux droites sont symétriques par rapport à un point alors elles sont parallèles Ici les droites (AB) et (A’B’) sont symétrique par rapport à M donc (AB) // (A’B’). Symétrique d’un angle. Si deux angles sont symétriques par rapport à un point alors ils ont la même mesure Ici les angles ABC et A’B’C’ sont symétrique par rapport à O donc ABC = A’B’C’. Symétrique d’un cercle. Le symétrique d’un cercle est un cercle de même rayon Sommaire A C'

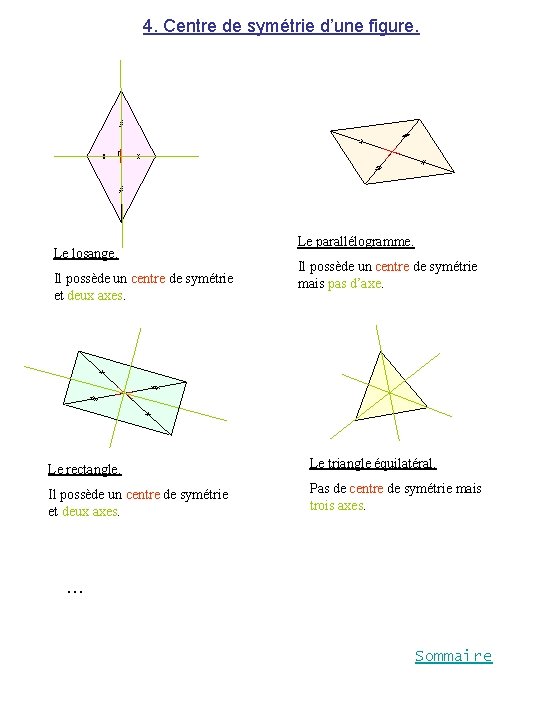
4. Centre de symétrie d’une figure. Le losange. Il possède un centre de symétrie et deux axes. Le parallélogramme. Il possède un centre de symétrie mais pas d’axe. Le rectangle. Le triangle équilatéral. Il possède un centre de symétrie et deux axes. Pas de centre de symétrie mais trois axes. … Sommaire








