Spektrala Transformer Introduktion svngningar fasvektorer DT 1130 Spektrala

Spektrala Transformer Introduktion svängningar & fasvektorer DT 1130 Spektrala Transformer • Jonas Beskow

När behövs spektrala transformer? • Kodning/komprimering: gsm, mp 3, jpeg, mpeg… • Audio/musik: syntes, effekter (reverb, pitch-shift…) • Talteknologi: talsyntes, taligenkänning, talkodning • Bildbehandling: bildförbättring, datorseende… DT 1130 Spektrala Transformer • Jonas Beskow

Harmoniska svängninar • Förekommer överallt i naturen • Återställande kraften proportionell mot avböjningen 1, 5 k m F x DT 1130 Spektrala Transformer • Jonas Beskow m

Harmoniska svängninar (forts. ) • Newtons rörelseekvation och Hooks lag ger DT 1130 Spektrala Transformer • Jonas Beskow

Summor av svängningar y(t) = sin ωt + sin ω(t + τ) ωτ = 0 ωτ = π ωτ = -1. 58 + + + = = = DT 1130 Spektrala Transformer • Jonas Beskow

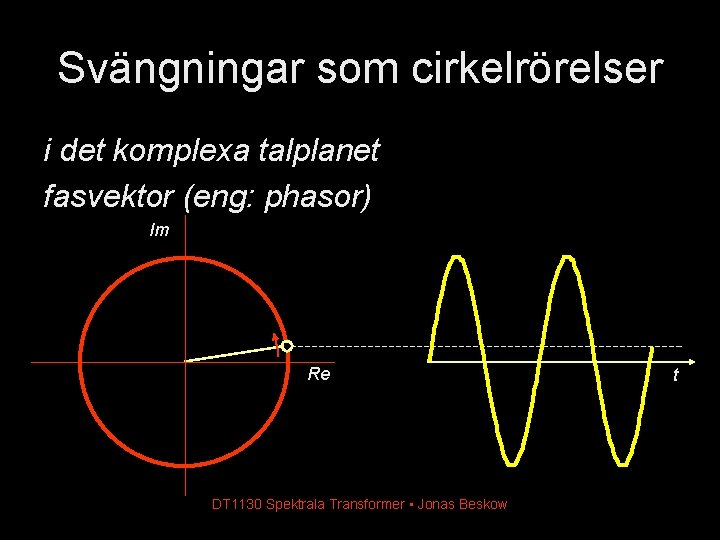
Svängningar som cirkelrörelser i det komplexa talplanet fasvektor (eng: phasor) Im Re DT 1130 Spektrala Transformer • Jonas Beskow t

Komplexa tal j 2 = -1 rektangulär form z = x + jy polär form z = r (cos θ + j sin θ) = re jθ Im y r θ x DT 1130 Spektrala Transformer • Jonas Beskow Re

Komplexa tal, räkneregler z 1 = x 1 + jy 1 z 2 = x 2 + jy 2 z 1 + z 2 = x 1 + x 2 + j(y 1 + y 2) z 1 z 2 = x 1 x 2 - y 1 y 2 + j(x 1 y 2 + x 2 y 1) polär form z 1 z 2 = r 1 e jθ 1 r 2 e jθ 2 = r 1 r 2 e j(θ 1 +θ 2) z 1 / z 2 = (r 1/r 2)e j(θ 1 -θ 2) Im y r θ DT 1130 Spektrala Transformer • Jonas Beskow x Re

Komplexa tal (forts. ) DT 1130 Spektrala Transformer • Jonas Beskow

Svängningsmoder hos en sträng y(x) = sin(πx/L) y(x) = sin(2πx/L) y(x) = sin(3πx/L) y(x) = sin(4πx/L) y(x) = sin(5πx/L). . . DT 1130 Spektrala Transformer • Jonas Beskow

Fourierserier • En periodisk vågform kan beskrivas som en summa av deltoner • Deltonerna är sinusvågor och med olika faslägen, amplituder och frekvenser DT 1130 Spektrala Transformer • Jonas Beskow

Fourierserier f(t) = a 1 cos t + b 1 sin t + a 2 cos 2 t + b 2 sin 2 t + a 3 cos 3 t + b 3 sin 3 t +… DT 1130 Spektrala Transformer • Jonas Beskow

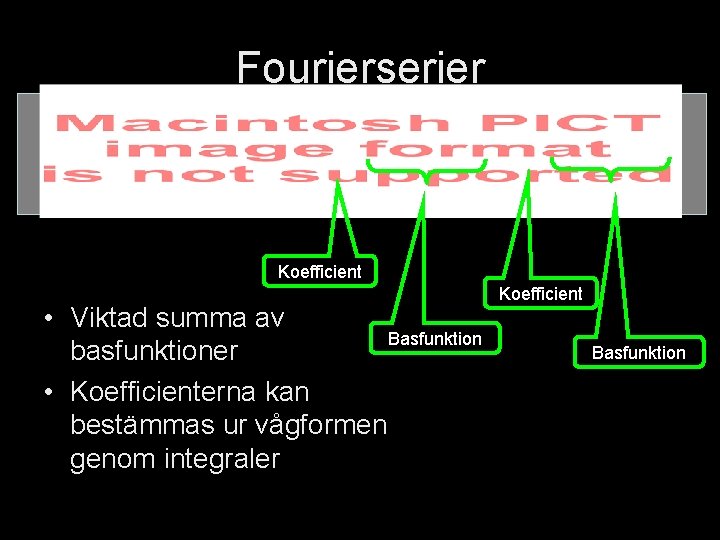
Fourierserier Koefficient • Viktad summa av Basfunktion basfunktioner • Koefficienterna kan bestämmas ur vågformen genom integraler Koefficient Basfunktion

Fourierserier (komplex form) Basfunktion Koefficient DT 1130 Spektrala Transformer • Jonas Beskow

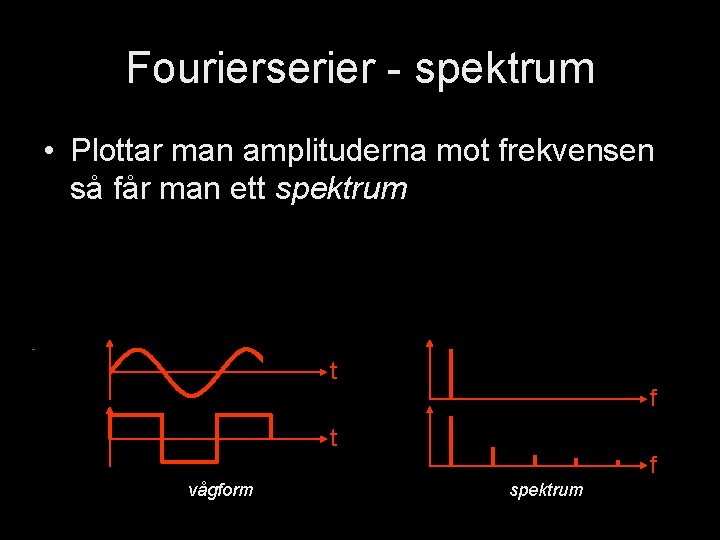
Fourierserier - spektrum • Plottar man amplituderna mot frekvensen så får man ett spektrum t f t vågform f spektrum

Fourierserier • Fourierserier är ett exempel på en Spektral Transform • Omvandlar mellan tids- och frekvensdomän Tidsdomän Frekvensdomän t f t vågform f spektrum

Vad då transformer? • En transform översätter mellan två koordinatsystem exempel: Den geometriska transformen p=x+y q = -x + y översätter punkten (x, y) till (p, q) y q DT 1130 Spektrala Transformer • Jonas Beskow p x

Transformer (forts. ) • En transform är en viktad summa av basvektorer • Rymderna – eller domänerna – som vi transformerar från och till kan ha godtyckligt många dimensioner. exempel: en samplad ljudsignal med N värden 1. . . N kan betraktas som en punkt i en N-dimensionell tidsdomän • En spektral transformerar mellan tidsdomänen och frekvensdomänen DT 1130 Spektrala Transformer • Jonas Beskow

Sammanfattning • Harmoniska svängningar kan representeras med en roterande komplex fasvektor (eng. phasor) • Vibration hos en sträng kan beskrivas med en summa av sinusformade stående vågor, svängningsmoder • Alla periodiska vågformer kan uttryckas med en fourierserie som en viktad summa av sinusvågor alt. fasvektorer DT 1130 Spektrala Transformer • Jonas Beskow